高中数学苏教版必修2课时2圆柱、圆锥和圆台word学案

高中数学苏教版必修2课时2圆柱、圆锥和圆台word学案

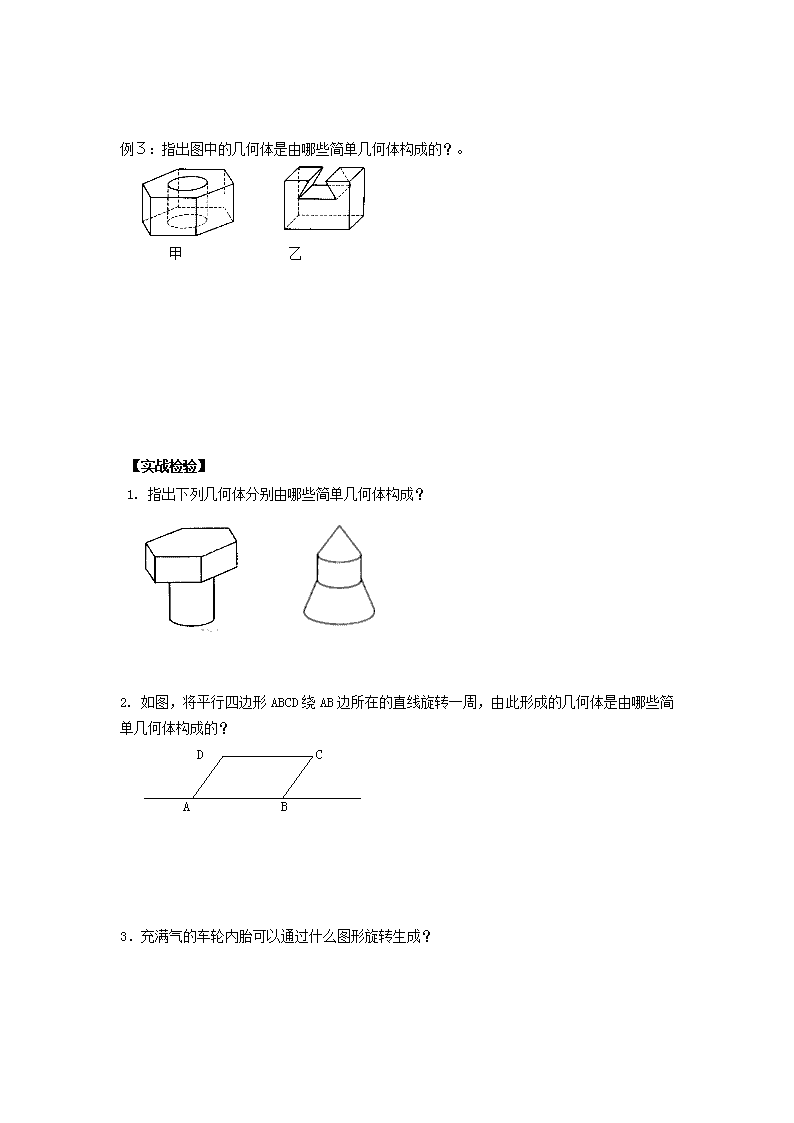
课时 2 圆柱、圆锥和圆台 【课标展示】 1．初步理解圆柱、圆锥、圆台和球的概念，掌握它们的生成规律； 2．了解圆柱、圆锥、圆台和球中一些常用名称的含义； 3．了解一些复杂几何体的组成情况，学会分析并掌握它们由哪些简单几何体组合而成； 4．结合日常生活中的一些具体实例，体会客观世界中事物与事物之间内在联系的辨证唯物 主义观点，初步学会用类比的思想分析问题和解决问题． 【先学应知】 1． 圆柱的定义： 母线 底面 轴 2．圆锥的定义： 3．圆台的定义： 4．球的定义： 5．旋转面的定义： 6．旋转体的定义： 7．将一个等腰梯形绕着它的较长的底边所在直线旋转一周，所得的几何体包括 8．用一个平面截一个几何体，不论怎样截，得到的都是圆面，则这个几何体是 【合作探究】 例 1：给出下列命题： 甲：圆柱两底面圆周上任意两点的连线是圆柱的母线； 乙：圆台的任意两条母线必相交； 丙：球面作为旋转面，只有一条旋转轴，没有母线。 其中正确的命题的有 （ ） A．0 B. 1 C. 2 D. 3 例 2：如图，将直角梯形 ABCD 绕 AB 边所在的直线旋转一周，由此形成的几何体是由哪些简 单几何体构成的？。 A B CD 例３：指出图中的几何体是由哪些简单几何体构成的？。 甲 乙 【实战检验】 1. 指出下列几何体分别由哪些简单几何体构成？ 2. 如图，将平行四边形 ABCD 绕 AB 边所在的直线旋转一周，由此形成的几何体是由哪些简 单几何体构成的？ D C A B 3．充满气的车轮内胎可以通过什么图形旋转生成？ 【课时作业 2】 1．一个圆柱的轴截面的面积为 S 的正方形，则圆柱的底面半径是 . 2．正方体的内切球与外接球（正方体的顶点都在球面上）的半径之比为 . 3．把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1: 4，母线长是 10，则圆锥的 母线长是 。 4．一个圆台的母线长为 5，上、下底面直径分别为 2、8，则圆台的高为 . 5．球的半径为 10 cm，若它的截面面积是 236 cm ，则球心到截面的距离是 . 6．一个圆台的两底面半径分别是 2 cm 和 5 cm，母线长是3 10cm ，则它的轴截面面 积是 . 7．已知球的外切圆台上、下底面的半径分别为 ,r R ，求球的半径. 8． 如果圆锥的侧面展开图是半圆，求这个圆锥的顶角（圆锥轴截面中两条母线的夹角）. 9．（探究创新题）已知一个圆锥的底面半径为 2 cm ，高为 6 cm ，在圆锥中有一个高为 xcm 的内接圆柱。 （1）用 x 表示圆柱的轴截面面积 S ；（2）当 x 为何值时， S 最大？ 10．若一个圆锥的轴截面是等边三角形，其面积为 3 ，求这个圆锥的全面积. 【疑点反馈】（通过本课时的学习、作业之后，还有哪些没有搞懂的知识，请记录下来） 第 2 课时 圆柱、圆锥和圆台 例 1 Ａ 【解】对于甲：圆柱的母线应和轴平行；对于乙：圆台的母线即为原圆锥的母线， 母线的延长线相交于一点，母线没有交点；对于丙：过球心的任何一条线都可以作为旋转轴， 它没有母线。 例 2 【解】圆锥和圆柱。 例 3 【解】甲：一个六棱柱挖去一个圆柱所得几何体，乙：一个长方体挖去一个四棱柱。 【实践检验】 1、答：左图是由一个六棱柱和一个圆柱构成；右图是由一个圆锥，一个圆柱，一个圆台构 成。 2、答：是由一个圆柱在左端增加一个圆锥而在右端挖出一个圆锥而得到的几何体。 3、答：一个圆绕一条直线旋转一周即得（该圆与该直线在同一平面内） 【课时作业 2】 答案：1． 2 S 2． 1: 3 解析：设正方体的棱长为 a ，则其内切球与外接球的半径分别为 3,2 2 a a 。 3． 40 3 解析：设圆锥的母线为 l ，截得圆台的上、下底面半径分别为 r ， 4r . 根据相似三角形的性质得， 10 4 l r l r   ，解得 40 3l  .所以，圆锥的母线长为 40 3 . 4． 4 5． 8 cm 6． 263cm 7．解：圆台轴截面为等腰梯形，与球的大圆相切，由此得 梯形腰长为 R+r，梯形的高即球的直径为 2 2( ) ( ) 2r R R r rR    ， 所以，球的半径为 rR . 8．解：设圆锥底面半径为 r，母线长为 l，依条件则有 2πr＝πl， 如图 2—2 ∴ 2 1 l r ，即∠ASO＝30°，因此圆锥顶角为 60°. 9．解: （1）如图轴截面为等腰三角 SEF,OE=2,SO=6, 1CC x ,则 由 1 ~ECC EOS  ,得 1 1CC EC SO EO  , 12 6 2 OCx  , 1 6 3 xOC  ,所以 2 (6 )3S x x  ； （2）由 22 2(6 ) ( 3) 63 3S x x x      ,所以当 3x  时，S 最大。 10．解：设等边三角形的边长为 a ，圆锥底面半径为 r， ∵S＝ 2 1 absinθ，∴ 2 1 a2sin60°＝ 3 ∴a2＝4，a＝2，a=2r ∴r＝1 图 2——2 S D E OC1 C FD1 S 全＝2πr＋πr2＝2π＋π＝3π.