河北省石家庄市康福外国语学校2019-2020学年高一上学期月考数学试题

河北省石家庄市康福外国语学校2019-2020学年高一上学期月考数学试题

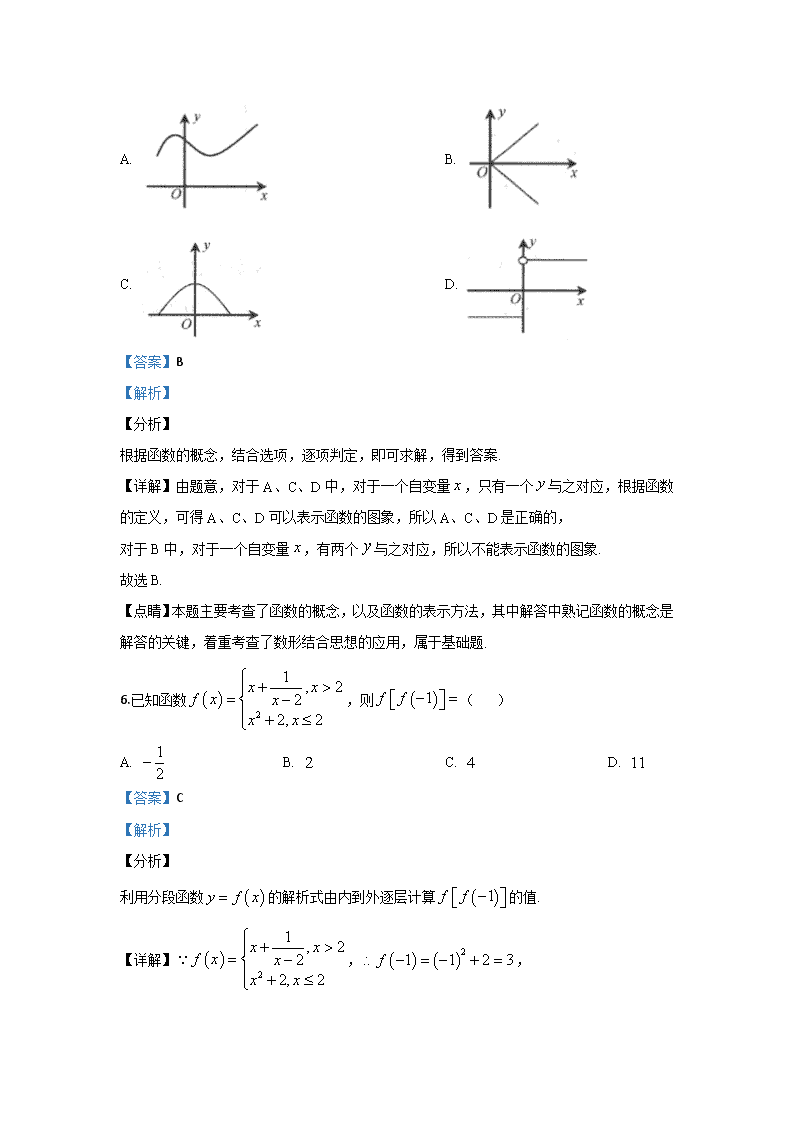
石家庄市康福外国语学校2019——2020学年度第一学期第二次月考 高一年级数学试卷 考试时间：120分钟 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上试卷满分：150分 第Ⅰ卷（选择题）‎ 一．选择题（共12小题，满分60分，每小题5分）‎ ‎1.已知集合，则满足条件集合的个数为（ ）‎ A. 2 B. ‎3 ‎C. 4 D. 8‎ ‎【答案】C ‎【解析】‎ ‎∵，又，∴集合的个数为个，故选C．‎ ‎2.已知集合，且，则等于（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由题意得出或，求出实数的值后，并代入集合，检验集合是否满足元素的互异性，由此可得出实数的值.‎ ‎【详解】集合，且，或，‎ 解得或 当时，，集合不满足互异性；‎ 当时，，，集合满足互异性.‎ 因此，实数.‎ 故选：C.‎ ‎【点睛】本题考查利用有限集中的元素求参数的值，在求出参数值之后，还应对有限集的元素是否满足互异性进行检验，考查运算求解能力，属于基础题.‎ ‎3.已知全集U={1，2，3，4，5，6}，A={1，2，6}，B={2，4，5}，则（∁UA）∩B=( )‎ A. {4，5} B. {1，2，3，4，5，6}‎ C. {2，4，5} D. {3，4，5}‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据补集及交集的运算法则求解即可.‎ ‎【详解】因为,所以（∁UA）∩B，故选A.‎ ‎【点睛】本题主要考查了集合的交集补集运算，属于容易题.‎ ‎4.函数f（x）=的定义域为（　　）‎ A. [3，+∞） B. [3，4）∪（4，+∞） C. （3，+∞） D. [3，4）‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 要使函数有意义，只需函数各个部分都有意义，即，解得,写出定义域即可.‎ ‎【详解】要使函数有意义，则，解得，故选B.‎ ‎【点睛】本题主要考查了函数的定义域，属于中档题.‎ ‎5.下列四个图象中，不是函数图象的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据函数的概念，结合选项，逐项判定，即可求解，得到答案.‎ ‎【详解】由题意，对于A、C、D中，对于一个自变量，只有一个与之对应，根据函数的定义，可得A、C、D可以表示函数的图象，所以A、C、D是正确的，‎ 对于B中，对于一个自变量，有两个与之对应，所以不能表示函数的图象.‎ 故选B.‎ ‎【点睛】本题主要考查了函数的概念，以及函数的表示方法，其中解答中熟记函数的概念是解答的关键，着重考查了数形结合思想的应用，属于基础题.‎ ‎6.已知函数，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 利用分段函数的解析式由内到外逐层计算的值.‎ ‎【详解】，，‎ 因此，.‎ 故选：C.‎ ‎【点睛】本题考查分段函数值的计算，在计算多层函数值时，遵循由内到外的原则逐层计算，考查计算能力，属于基础题.‎ ‎7.已知函数f(x)=2x2-mx+3，当时是增函数，当时是减函数，则f(1)等于 ( )‎ A. -3 B. ‎13 ‎C. 7 D. 含有m的变量 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由函数单调区间,可得函数的对称轴,进而求出函数参数,然后即可求出函数值.‎ ‎【详解】由函数在上是增函数,在上是减函数,得函数的对称轴为,又因二次函数的对称轴为,所以由,得,‎ 所以,‎ 故选:B.‎ ‎【点睛】本题考查了二次函数的性质的应用,由二次函数的单调区间求对称轴是解题的关键,属于基础题.‎ ‎8.已知，，，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据函数的单调性及特殊值即可比较三数的大小.‎ ‎【详解】因为，，，‎ 所以 故选D ‎【点睛】本题主要考查了指数函数，对数函数的单调性，及特殊值在比较大小中的应用，属于中档题.‎ ‎9.已知且函数的图象恒过定点，若点在幂函数的图象上，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由真数等于，求出定点的坐标，设，将点的坐标代入函数的解析式，求出的值，可得出函数的解析式，由此可计算出的值.‎ ‎【详解】令，得，当时，，所以点的坐标为，‎ 由于函数为幂函数，设，‎ 将点的坐标代入函数的解析式，得，则，‎ ‎，因此，.‎ 故选：C.‎ ‎【点睛】本题考查对数型函数过定点问题，同时也考查了幂函数值的计算，解题的关键就是求出幂函数的解析式，考查计算能力，属于基础题.‎ ‎10.若函数f（x）对于任意实数x恒有f（x）﹣‎2f（﹣x）=3x﹣1，则f（x）等于（　　）‎ A. x+1 B. x﹣‎1 ‎C. 2x+1 D. 3x+3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据题意，可得，与已知方程联立方程组，把 视作未知数，即可求解.‎ ‎【详解】因为，所以，联立方程组，解得，故选A.‎ ‎【点睛】本题主要考查了函数解析式的求法，属于中档题.‎ ‎11.已知函数f（x）=在R上单调递增，则实数a的取值范围是（　　）‎ A. [﹣1，+∞） B. （﹣1，+∞） C. [﹣1，0） D. （﹣1，0）‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据分段函数的单调性，函数在R上单调递增，需要每段都单调递增且左段的右端点函数值不大于右段的左端点的函数值，即可求出a的取值范围.‎ ‎【详解】因为函数在R上是递增函数，所以，解得，故选C.‎ ‎【点睛】本题主要考查了分段函数的单调性，属于中档题.‎ ‎12.已知偶函数的定义域为，且在上是减函数，，则实数的取值范围是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据函数为偶函数，判断出函数在 上的单调性，利用单调性和对称性列不等式组，解不等式组求得的取值范围.‎ ‎【详解】∵为偶函数，且在上是减函数，∴在上是增函数.‎ 可化为，‎ ‎∵为偶函数，∴即为.‎ 又在上为减函数，∴‎ 解得.‎ 故选C.‎ ‎【点睛】本小题主要考查偶函数的单调性和对称性，考查化归与转化的数学思想方法，属于基础题.‎ 第Ⅱ卷（非选择题）‎ 二、填空题（共4小题，满分20分，每小题5分）‎ ‎13.计算_____．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用指数、对数的运算法则可计算出所求代数式的值.‎ ‎【详解】原式.‎ 故答案为：.‎ ‎【点睛】本题考查指数与对数的计算，熟悉指数与对数的运算律是计算的关键，考查计算能力，属于基础题.‎ ‎14..若集合，，则集合_________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由，化简集合B ,然后求交集即可.‎ ‎【详解】因为，所以，即，所以，故填.‎ ‎【点睛】本题主要考查了集合的化简，集合的交集运算，属于中档题.‎ ‎15. 已知函数f(x)的定义域为(－1，0)，则函数f(2x＋1)的定义域为________．‎ ‎【答案】‎ ‎【解析】‎ 由－1<2x＋1<0，得－1

查看更多