高考数学二轮复习教案：第二编 专题二 第1讲 三角函数的图象与性质

高考数学二轮复习教案：第二编 专题二 第1讲 三角函数的图象与性质

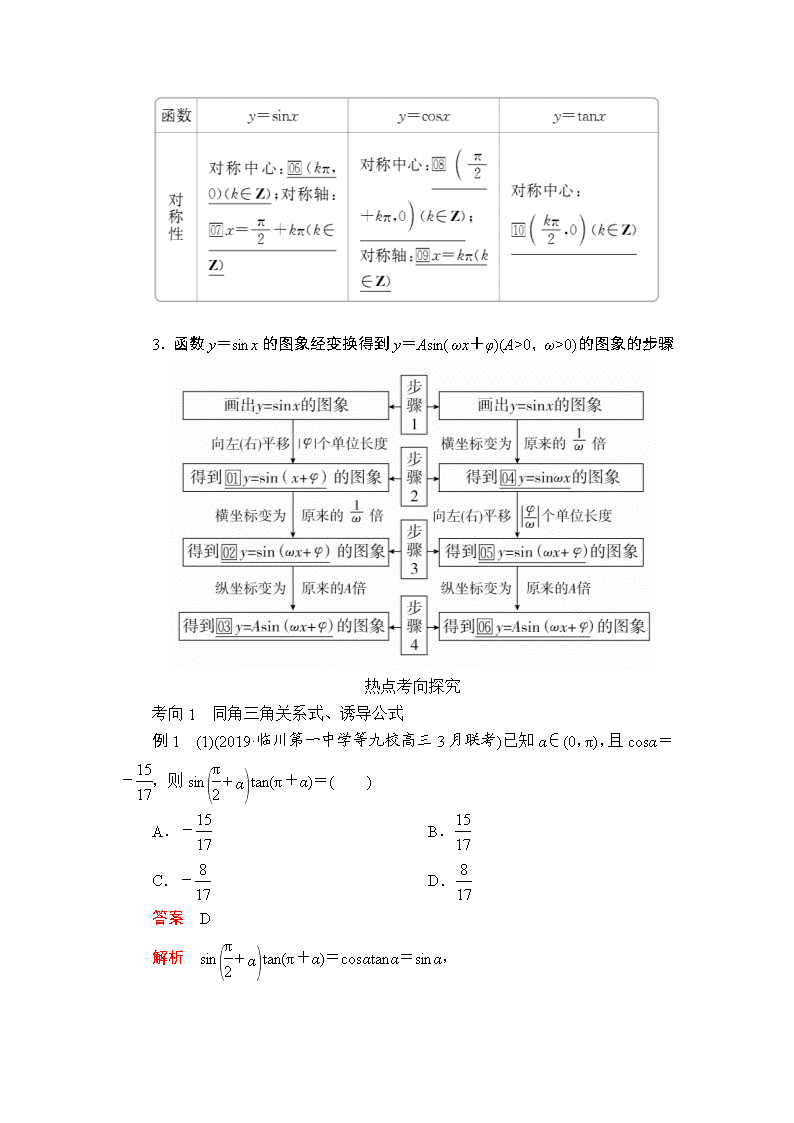
专题二 三角函数、解三角形与平面向量 第1讲　三角函数的图象与性质 ‎「考情研析」　　1.以图象为载体，考查三角函数的最值、单调性、对称性、周期性．　2.考查三角函数式的化简、三角函数的图象和性质、角的求值，重点考查分析、处理问题的能力，是高考的必考点.‎ 核心知识回顾 ‎1.同角关系式与诱导公式 ‎(1)同角三角函数的基本关系：sin2α＋cos2α＝1，＝tanα.‎ ‎(2)诱导公式：在＋α，k∈Z的诱导公式中“奇变偶不变，符号看象限”．‎ ‎2．三种三角函数的性质 ‎3．函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的步骤 热点考向探究 考向1 同角三角关系式、诱导公式 例1　(1)(2019·临川第一中学等九校高三3月联考)已知α∈(0，π)，且cosα＝－，则sintan(π＋α)＝(　　)‎ A．－ B． C．－ D． 答案　D 解析　sintan(π＋α)＝cosαtanα＝sinα，‎ 因为α∈(0，π)，且cosα＝－，‎ 所以sinα＝＝＝.故选D.‎ ‎(2)已知sinα－cosα＝，α∈(0，π)，则tanα＝(　　)‎ A．－1 B．－ C． D．1‎ 答案　A 解析　因为sinα－cosα＝，所以(sinα－cosα)2＝2，所以sin2α＝－1.因为α∈(0，π)，2α∈(0,2π)，所以2α＝，即α＝，故tanα＝－1.‎ ‎(3)已知α为锐角，且有2tan(π－α)－3cos＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sinα＝(　　)‎ A. B． C． D．－ 答案　C 解析　由已知可得，‎ ‎－2tanα＋3sinβ＋5＝0，　①‎ tanα－6sinβ－1＝0，　②‎ ‎①×2＋②得tanα＝3.∵α为锐角，∴sinα＝.故选C.‎ ‎(1)利用诱导公式化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐，特别注意函数名称和符号的确定．‎ ‎(2)应用公式时注意方程思想的应用：对于sinα＋cosα，sinαcosα，sinα－cosα这三个式子，利用(sinα±cosα)2＝1±2sinαcosα，可以知一求二．‎ ‎(3)关于sinα，cosα的齐次式，往往转化为关于tanα的式子求解．‎ ‎1．(2019·内江市高三第三次模拟)已知α∈，sinα＝，则tan＝(　　)‎ A．7 B． C．－7 D．－ 答案　D 解析　∵α∈，sinα＝，∴cosα＝－，∴tanα＝－.∴tan＝＝－.故选D.‎ ‎2．已知sin2α＝，则tanα＋等于(　　)‎ A. B． C． D．4‎ 答案　A 解析　由sin2α＝2sinαcosα＝，可得sinαcosα＝，所以tanα＋＝＋＝＝.故选A.‎ ‎3．如果f(tanx)＝sin2x－5sinxcosx，那么f(2)＝________.‎ 答案　－ 解析　∵f(tanx)＝sin2x－5sinxcosx＝＝，∴f(x)＝，则f(2)＝－.‎ 考向2 三角函数的图象及应用 例2　(1)(2019·永州市高三第三次模拟)将函数f(x)＝sin2x＋cos2x图象上各点的横坐标伸长到原来的2倍，所得函数的一个对称中心可以是(　　)‎ A. B．(0,0)‎ C. D． 答案　A 解析　f(x)＝sin2x＋cos2x＝2sin，将横坐标伸长到原来的2倍，所得函数为g(x)＝2sin，令x＋＝kπ(k∈Z)⇒x＝kπ－(k∈Z)，则对称中心为，k∈Z，令k＝0，则其中一个对称中心为.故选A.‎ ‎(2)函数f(x)＝Asin(ωx＋φ)(A，ω，φ是常数，A>0，ω>0)的部分图象如图所示，则f(x)的单调递增区间为________．‎ 答案　，k∈Z 解析　由函数的图象可得A＝，T＝－＝·，解得ω＝2.再根据五点作图法可知2×＋φ＝π，φ＝，所以f(x)＝sin.由－＋2kπ≤2x＋≤＋2kπ(k∈Z)，可得－＋kπ≤x≤＋kπ(k∈Z)．‎ ‎1．解析式y＝Asin(ωx＋φ)＋B的确定方法 ‎(1)A，B由最值确定，即A＝，‎ B＝.‎ ‎(2)ω由函数周期确定，相邻两对称轴(或两对称中心)之间的距离为，对称轴与相邻对称中心之间的距离为.‎ ‎(3)φ由图象上的特殊点确定，利用五点作图的五个特殊点直接确定．‎ ‎2．三角函数图象平移问题处理策略 ‎(1)看平移要求：首先要看题目要求由哪个函数平移得到哪个函数，这是判断移动方向的关键点．‎ ‎(2)看移动方向：移动的方向一般记为“正向左，负向右”，看y＝Asin(ωx＋φ)中φ的正负和它的平移要求．‎ ‎(3)看移动单位：在函数y＝Asin(ωx＋φ)中，周期变换和相位变换都是沿x轴方向的，所以ω和φ之间有一定的关系，φ是初相，再经过ω的压缩，最后移动的单位是.‎ ‎1．(2019·唐山市高三第二次模拟)已知函数f(x)＝sin(ω>0)的最小正周期为π，把f(x)的图象向左平移个单位后，所得函数图象的一条对称轴为(　　)‎ A．x＝0 B．x＝ C．x＝ D．x＝ 答案　B 解析　∵函数f(x)＝sin(ω＞0)的最小正周期为＝π，∴ω＝1，f(x)＝sin.若将函数f(x)的图象向左平移个单位，可得y＝sin＝sin的图象，令2x＋＝kπ＋，k∈Z，求得x＝＋，令k＝0，可得所得函数图象的一条对称轴为x＝.故选B.‎ ‎2．(2019·丹东市高三总复习质量测试(一))设函数f(x)＝sinωx(ω>0)，已知对于内的任意x1，总存在内的x2，使得f(x1)＋f(x2)＝0，则ω的(　　)‎ A．最大值为3 B．最小值为3‎ C．最大值为 D．最小值为 答案　D 解析　因为要满足对任意的x1∈，总存在x2∈，使得f(x1)＋f(‎ x2)＝0，对于f(x)＝sinωx(ω>0)，则在上的函数值有正值，即f(x1)可以有正值，要存在x2使得f(x1)＋f(x2)＝0，则f(x2)需要有负值．又f(x1)可以取到最大值1，要存在f(x2)，使得f(x1)＋f(x2)＝0，则f(x2)要可以取到最小值－1，说明f(x)在x>0上取得第一个最小值的点应在的左侧或者恰好落在处，所以T≤，即·≤，解得ω≥.故选D.‎ 考向3 三角函数的性质 例3　(1)(2019·天津九校高三联考)已知函数f(x)＝sinωx－cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于，若将函数y＝f(x)的图象向左平移个单位得到函数y＝g(x)的图象，则y＝g(x)是减函数的区间为(　　)‎ A. B． C. D． 答案　D 解析　f(x)＝sinωx－cosωx＝2sin，因为图象与x轴的两个相邻交点的距离等于＝，所以T＝π，ω＝2，所以f(x)＝2sin.所以g(x)＝2sin＝2sin2x.由＋2kπ≤2x≤＋2kπ(k∈Z)，得＋kπ≤x≤＋kπ，所以y＝g(x)是减函数的区间为(k∈Z)．分析选项只有D符合．故选D.‎ ‎(2)若将函数y＝sin的图象向右平移m(m>0)个单位长度后所得的图象关于直线x＝对称，则m的最小值为(　　)‎ A. B． C． D． 答案　B 解析　平移后所得的函数图象对应的解析式是y＝sin ‎，如果该函数的图象关于直线x＝对称，则2＝kπ＋(k∈Z)，所以m＝－＋(k∈Z)，‎ 又m>0，故当k＝0时，m最小，此时m＝.‎ ‎(3)已知函数f(x)＝|sinx|·cosx，则下列说法正确的是(　　)‎ A．f(x)的图象关于直线x＝对称 B．f(x)的周期为π C．若|f(x1)|＝|f(x2)|，则x1＝x2＋2kπ(k∈Z)‎ D．f(x)在区间上单调递减 答案　D 解析　因为f(x)＝|sinx|·cosx，所以函数f(x)在区间[0,2π]上的解析式为f(x)＝ 且 f(x)是偶函数，画出f(x)的大致图象(图略)可知D选项正确．故选D.‎ 求解函数y＝Asin(ωx＋φ)的性质问题的三种意识 ‎(1)转化意识：利用三角恒等变换将所求函数转化为f(x)＝Asin(ωx＋φ)的形式．‎ ‎(2)整体意识：类比y＝sinx的性质，只需将y＝Asin(ωx＋φ)中的“ωx＋φ”看成y＝sinx中的“x”，采用整体代入求解．‎ ‎①令ωx＋φ＝kπ＋(k∈Z)，可求得对称轴方程．‎ ‎②令ωx＋φ＝kπ(k∈Z)，可求得对称中心的横坐标．‎ ‎③将ωx＋φ看作整体，可求得y＝Asin(ωx＋φ)的单调区间，注意ω的符号．‎ ‎(3)讨论意识：当A为参数时，求最值应分情况讨论A>0，A<0.‎ ‎1．已知函数f(x)＝sin(ωx＋φ)(0<ω<1，|φ|<π)．若对任意x∈R，f(1)≤f(x)≤f(6)，则(　　)‎ A．f(1016)－f(1017)>0‎ B．f(1016)－f(1017)＝0‎ C．f(1016)＋f(1017)<0‎ D．f(1016)＋f(1017)＝0‎ 答案　A 解析　∵0<ω<1，∴函数f(x)的最小正周期T>2π.∵对任意x∈R，‎ f(1)≤f(x)≤f(6)，∴f(1)＝－1，f(6)＝1，函数f(x)在区间[1,6]上单调递增，∴＝6－1＝5，即T＝10.∴f(1016)＝f(6)，f(1017)＝f(7)．又∵函数f(x)的图象关于直线x＝6对称，∴f(1017)＝f(7)＝f(5)．∵函数f(x)在区间[1,6]上单调递增，∴f(5)f(1017)，∴f(1016)－f(1017)>0.故选A.‎ ‎2．(2019·宁夏银川高三下学期质检)将函数f(x)＝sin2x＋cos2x的图象向左平移个单位得到g(x)的图象，则g(x)在下列哪个区间上单调递减(　　)‎ A. B． C. D． 答案　C 解析　将函数f(x)＝sin2x＋cos2x＝sin的图象向左平移个单位得到g(x)＝sin＝sin＝cos2x，在区间上，则2x∈[－π，0]，g(x)单调递增，故A不满足条件；在区间上，则2x∈，g(x)不单调，故B不满足条件；在区间上，则2x∈[0，π]，g(x)单调递减，故C满足条件；在区间上，则2x∈[π，2π]，g(x)单调递增，故D不满足条件．故选C.‎ ‎3．(2019·新疆乌鲁木齐高三第二次质量检测)若关于x的方程(sinx＋cosx)2＋cos2x＝m在区间[0，π)上有两个根x1，x2，且|x1－x2|≥，则实数m的取值范围是(　　)‎ A．[0,2) B．[0,2]‎ C．[1，＋1] D．[1，＋1)‎ 答案　B 解析　关于x的方程(sinx＋cosx)2＋cos2x＝m在区间[0，π)上有两个根x1，x2，方程即sin2x＋cos2x＝m－1，即sin＝，∴sin＝在区间[0，π)上有两个根x1，x2，且|x1－x2|≥.∵x∈[0，π)，∴2x＋∈∪∪，∴－‎ eq f( (2),2)≤≤，求得0≤m≤2.故选B.‎ ‎真题押题 ‎『真题模拟』‎ ‎1．(2019·新乡市二模)已知sin2θ＋2cosθ＝－2，那么cos2θ－2sinθ＝(　　)‎ A．1 B．－2‎ C．－1 D．2‎ 答案　A 解析　因为sin2θ＋2cosθ＋2＝0，所以cos2θ－2cosθ－3＝0，解得cosθ＝－1或cosθ＝3(舍去)，所以sinθ＝0，所以cos2θ－2sinθ＝1.故选A.‎ ‎2．(2019·天津高考)已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<π)是奇函数，将y＝f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g(x)．若g(x)的最小正周期为2π，且g＝，则f＝(　　)‎ A．－2 B．－ C． D．2‎ 答案　C 解析　因为f(x)是奇函数(显然定义域为R)，所以f(0)＝Asinφ＝0，所以sinφ＝0.又|φ|<π，所以φ＝0.由题意得g(x)＝Asin，且g(x)的最小正周期为2π，所以ω＝1，即ω＝2.所以g(x)＝Asinx，所以g＝Asin＝A＝，所以A＝2.所以f(x)＝2sin2x，所以f＝.故选C.‎ ‎3. (2019·汉中市高三教学质量第二次检测)函数f(x)＝cos(ωx＋φ)的部分图象如图所示，则函数f(x)的单调递增区间为(　　)‎ A.(k∈Z)‎ B.(k∈Z)‎ C.(k∈Z)‎ D.(k∈Z)‎ 答案　D 解析　由图可知，图象过，⇒＝－⇒T＝π，∵T＝，ω>0，∴ω＝2；图象过，∴cos＝0，根据题中图象可得2×＋φ＝2mπ＋(m∈Z)，即φ＝2mπ－.因为|φ|<，所以φ＝－，所以f(x)＝cos，当2kπ－π≤2x－≤2kπ(k∈Z)时，函数单调递增，化简得kπ－≤x≤kπ＋(k∈Z)．故选D.‎ ‎4．(2019·温州质检)函数f(x)＝2x－tanx在上的图象大致为(　　)‎ 答案　C 解析　因为函数f(x)＝2x－tanx为奇函数，所以函数图象关于原点对称，排除A，B，又当x→时，y<0，排除D.故选C.‎ ‎5．(2019·全国卷Ⅲ)设函数f(x)＝sin(ω>0)，已知f(x)在[0,2π]有且仅有5个零点，下述四个结论：‎ ‎①f(x)在(0,2π)有且仅有3个极大值点；‎ ‎②f(x)在(0,2π)有且仅有2个极小值点；‎ ‎③f(x)在单调递增；‎ ‎④ ω的取值范围是.‎ 其中所有正确结论的编号是(　　)‎ A．①④ B．②③‎ C．①②③ D．①③④‎ 答案　D 解析　已知f(x)＝sin(ω>0)在[0,2π]有且仅有5个零点，如图，其图象的右端点的横坐标在[a，b)上，此时f(x)在(0,2π)有且仅有3个极大值点，但f(x)在(0,2π)可能有2或3个极小值点，所以①正确，②不正确；当x∈[0,2π]时，ωx＋∈，由f(x)在[0,2π]有且仅有5个零点可得5π≤2πω＋<6π，得ω的取值范围是，所以④正确；当x∈时，<ωx＋<＋<<，所以f(x)在单调递增，所以③正确．故选D.‎ ‎6．(2018·全国卷Ⅱ)已知tan＝，则tanα＝________.‎ 答案　 解析　tan＝＝＝，解方程得tanα＝.‎ ‎『金版押题』‎ ‎7．若将函数f(x)＝sinxcosx＋cos2x－的图象向右平移φ(φ>0)个单位，所得图象关于y轴对称，则φ的最小值是(　　)‎ A. B． C． D． 答案　D 解析　∵f(x)＝sinxcosx＋cos2x－＝sin2x＋－＝sin2x＋cos2x＝sin，函数f(x)的图象向右平移φ个单位可得 y＝sin＝sin，所得图象关于y轴对称，‎ 根据三角函数的对称性，可得此函数在y轴处取得函数的最值，即sin＝±1，解得－2φ＋＝＋kπ，k∈Z，‎ 所以φ＝－－，k∈Z，且φ>0，令k＝－1，得φ的最小值为.故选D.‎ ‎8．已知函数f(x)＝－2sin(2x＋φ)(|φ|<π)，若f＝－2，则f(x)的一个单调递减区间是(　　)‎ A. B． C. D． 答案　C 解析　由f＝－2，得f＝－2sin＝－2sin＝－2，所以sin＝1.因为|φ|<π，所以φ＝.由2kπ－≤2x＋≤2kπ＋，k∈Z，解得kπ－≤x≤kπ＋，k∈Z.当k＝0时，－≤x≤.故选C.‎ 配套作业 一、选择题 ‎1．已知α为锐角，且sinα＝，则cos(π＋α)＝(　　)‎ A．－ B． C．－ D． 答案　A 解析　因为α为锐角，且sinα＝，所以cosα＝.所以cos(π＋α)＝－cosα＝－.‎ ‎2．函数f(x)＝tan的单调递增区间是(　　)‎ A.(k∈Z)‎ B.(k∈Z)‎ C.(k∈Z)‎ D.(k∈Z)‎ 答案　B 解析　当kπ－<2x－0，故α∈，故cosα＝，所以＝－.‎ ‎4．如果存在正整数ω和实数φ使得函数f(x)＝sin2(ωx＋φ ‎)的图象如图所示(图象经过点(1,0))，那么ω的值为(　　)‎ A．1 B．2‎ C．3 D．4‎ 答案　B 解析　因为f(x)＝sin2(ωx＋φ)＝－cos[2(ωx＋φ)]，所以函数f(x)的最小正周期T＝＝，由题图知<1，且>1，即0，故排除C，故选A.‎ ‎6．(2019·毛坦厂中学高三校区联考)已知函数f(x)＝Asin(ωx＋φ)的图象与y轴交于点M，距离y轴最近的最大值点为N，若x1，x2∈(－a，a)，且x1≠x2，恒有f(x1)≠f(x2)，则实数a的最大值为(　　)‎ A. B． C． D． 答案　C 解析　由题意，得A＝3,3sinφ＝，|φ|<，∴φ＝，由五点作图法知×ω＋＝，解得ω＝3，∴f(x)＝3sin，令2kπ－≤3x＋≤2kπ＋，k∈Z.解得－≤x≤＋，k∈Z.∴(－a，a)⊆，∴00)的图象向左平移个单位得到函数g(x)的图象，若函数g(x)的图象关于直线x＝ω对称且在区间(－ω，ω)内单调递增，则ω的值为(　　)‎ A. B． C． D． 答案　A 解析　由题意得g(x)＝sin＝sin，因为函数g(x)的图象关于直线x＝ω对称且在区间(－ω，ω)内单调递增，所以ω2＋＝＋kπ(k∈Z)，－＋2mπ≤－ω2＋，ω2＋≤＋2mπ(m∈Z)，因此k≥0，kπ≤－2mπ，kπ≤2mπ，从而0≤－2mπ，0≤2mπ，即0≤m≤，所以m＝0，k＝0，ω＝，故选A.‎ ‎10．(2019·广元市高三第二次高考适应性统考)函数f(x)＝sin2x－(cos2x－sin2x)的图象为C，给出如下四个结论：‎ ‎①f(x)的最小正周期为π；‎ ‎②对任意的x∈R，都有f＋f＝0；‎ ‎③f(x)在上是增函数；‎ ‎④由y＝2sin2x的图象向右平移个单位长度可以得到图象C.‎ 其中所有正确结论的编号是(　　)‎ A．①② B．③④‎ C．①②③ D．①②③④‎ 答案　C 解析　f(x)＝sin2x－(cos2x－sin2x)＝sin2x－cos2x＝2sin，f(x)的最小正周期为＝π，故①正确；f＝2sin＝2sin0＝0，即函数图象关于点对称，即对任意的x∈R，都有f＋f＝0成立，故②正确；若x∈，则2x∈，2x－∈，此时函数f(x)为增函数，即f(x)在上是增函数，故③正确；由y＝2sin2x的图象向右平移个单位长度得到y＝2sin＝2sin，故④错误，故正确的是①②③，故选C.‎ ‎11．将函数f(x)＝2sin的图象向左平移个单位长度，再向上平移1个单位长度，得到g(x)的图象，若g(x1)g(x2)＝9，且x1，x2∈[－2π，2π]，则2x1－x2的最大值为(　　)‎ A. B． C． D． 答案　B 解析　由题意可得，g(x)＝2sin＋1，所以g(x)max＝3，又g(x1)g(x2)＝9，所以g(x1)＝g(x2)＝3，由g(x)＝2sin＋1＝3，得2x＋＝＋2kπ(k∈Z)，即x＝＋kπ(k∈Z)，因为x1，x2∈[－2π，2π]，所以(2x1－x2)max＝2×－＝，故选B.‎ 二、填空题 ‎12．(2019·南宁市高三模拟)已知＝5，则sin2α－sinαcosα＝________.‎ 答案　 解析　由已知可得sinα＋3cosα＝5(3cosα－sinα)，即sinα＝2cosα，所以tanα＝＝2，从而sin2α－sinαcosα＝＝＝＝.‎ ‎13．(2019·云南省高中毕业生统一检测)已知函数f(x)＝sinx＋cosx在[－m，m]上是单调递增函数，则f(2m)的取值范围为________．‎ 答案　[1,2]‎ 解析　函数f(x)＝sinx＋cosx＝2sin，‎ 由2kπ－≤x＋≤2kπ＋，k∈Z⇒2kπ－≤x≤2kπ＋，k∈Z，故f(x)在区间(k∈Z)上单调递增，当k＝0，f(x)在区间上是单调递增函数，则[－m，m]⊆，‎ ‎∴ f(2m)＝2sin，而<2m＋≤，‎ 所以≤sin≤1，所以f(2m)∈[1,2]．‎ ‎14．若函数f(x)＝sin(ωx＋φ)在区间上是单调递减函数，且函数值从1减小到－1，则f＝________.‎ 答案　 解析　由题意可得，函数的周期为2×＝π，即＝π，∴ω＝2，∴f(x)＝sin(2x＋φ)．由sin＝1，|φ|<可得φ＝，∴f(x)＝sin，∴f＝sin＝cos＝.‎ ‎15．已知函数f(x)＝Asin(ωx＋φ) 的部分图象如图所示，将函数y＝f(x)的图象向左平移个单位长度，得到函数y＝g(x)的图象，则g(π)＝________，函数y＝g(x)在区间上的最大值为________．‎ 答案　0　 解析　由题图可知函数y＝f(x)的周期为4π，‎ ‎∴ω＝.‎ 又∵点，在函数y＝f(x)的图象上，‎ ‎∴且|φ|<，∴φ＝－，A＝3，‎ 则f(x)＝3sin.‎ ‎∴g(x)＝3sin＝3cos，g(π)＝0.‎ 由x∈，可得∈，‎ 则3cos∈，即g(x)的最大值为.‎