高三数学总复习学案10
学案10 函数的图像
导学目标: 1.掌握作函数图象的两种基本方法:描点法,图象变换法.2.掌握图象变换的规律,能利用图象研究函数的性质.
自主梳理
1.应掌握的基本函数的图象有:一次函数、二次函数、幂函数、指数函数、对数函数等.
2.利用描点法作图:①确定函数的定义域;②化简函数的解析式;③讨论函数的性质(__________、__________、__________);④画出函数的图象.
3.利用基本函数图象的变换作图:
(1)平移变换:函数y=f(x+a)的图象可由y=f(x)的图象向____(a>0)或向____(a<0)平移____个单位得到;函数y=f(x)+a的图象可由函数y=f(x)的图象向____(a>0)或向____(a<0)平移____个单位得到.
(2)伸缩变换:函数y=f(ax) (a>0)的图象可由y=f(x)的图象沿x轴伸长(0
0)的图象可由函数y=f(x)的图象沿y轴伸长(____)或缩短(________)为原来的____倍得到.(可以结合三角函数中的图象变换加以理解)
(3)对称变换:①奇函数的图象关于________对称;偶函数的图象关于____轴对称;
②f(x)与f(-x)的图象关于____轴对称;
③f(x)与-f(x)的图象关于____轴对称;
④f(x)与-f(-x)的图象关于________对称;
⑤f(x)与f(2a-x)的图象关于直线________对称;
⑥曲线f(x,y)=0与曲线f(2a-x,2b-y)=0关于点________对称;
⑦|f(x)|的图象先保留f(x)原来在x轴________的图象,作出x轴下方的图象关于x轴的对称图形,然后擦去x轴下方的图象得到;
⑧f(|x|)的图象先保留f(x)在y轴________的图象,擦去y轴左方的图象,然后作出y轴右方的图象关于y轴的对称图形得到.
自我检测
1.(2009·北京)为了得到函数y=lg的图象,只需把函数y=lg x的图象上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
2.(2011·烟台模拟)已知图1是函数y=f(x)的图象,则图2中的图象对应的函数可能是
( )
A.y=f(|x|) B.y=|f(x)|
C.y=f(-|x|) D.y=-f(-|x|)
3.函数f(x)=-x的图象关于 ( )
A.y轴对称 B.直线y=-x对称
C.坐标原点对称 D.直线y=x对称
4.使log2(-x)0且a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一坐标系内的大致图象是 ( )
探究点一 作图
例1 (1)作函数y=|x-x2|的图象;
(2)作函数y=x2-|x|的图象;
(3)作函数的图象.
变式迁移1 作函数y=的图象.
探究点二 识图
例2 (1)函数y=f(x)与函数y=g(x)的图象如图,
则函数y=f(x)·g(x)的图象可能是 ( )
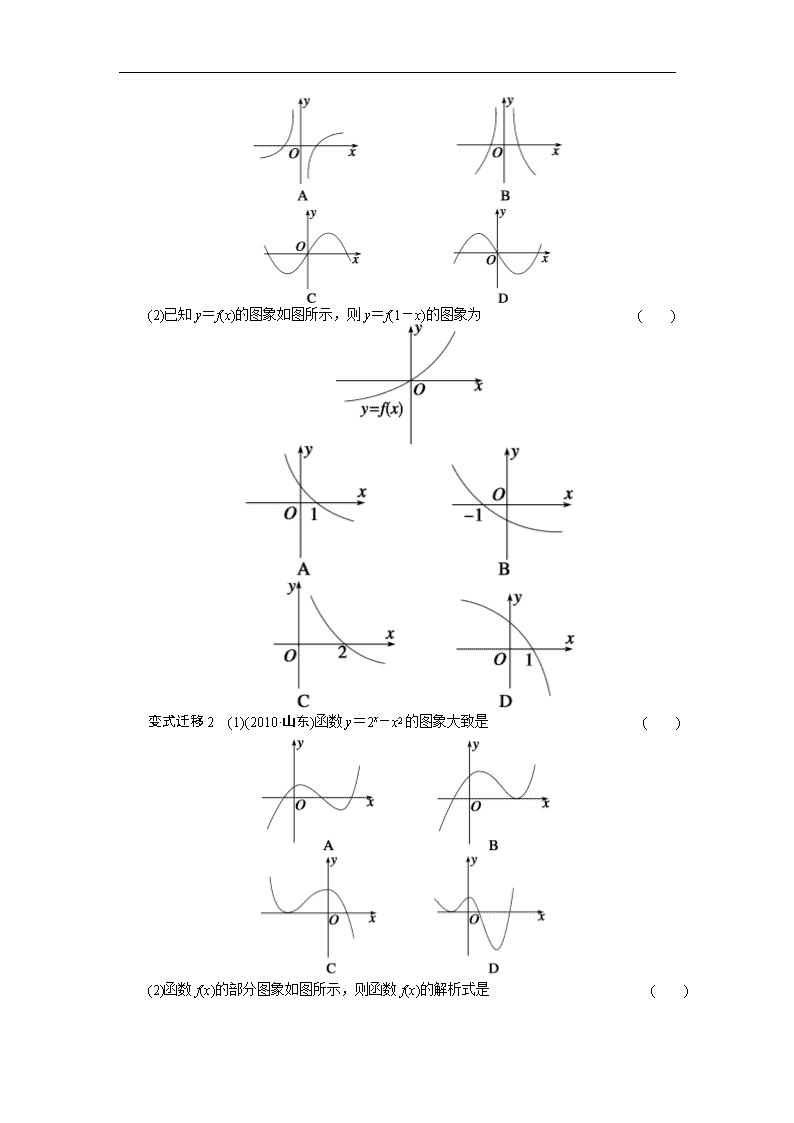
(2)已知y=f(x)的图象如图所示,则y=f(1-x)的图象为 ( )
变式迁移2 (1)(2010·山东)函数y=2x-x2的图象大致是 ( )
(2)函数f(x)的部分图象如图所示,则函数f(x)的解析式是 ( )
A.f(x)=x+sin x
B.f(x)=
C.f(x)=xcos x
D.f(x)=x·(x-)·(x-)
探究点三 图象的应用
例3 若关于x的方程|x2-4x+3|-a=x至少有三个不相等的实数根,试求实数a的取值范围.
变式迁移3 (2010·全国Ⅰ)直线y=1与曲线y=x2-|x|+a有四个交点,则a的取值范围是________.
数形结合思想的应用
例 (5分)(2010·北京东城区一模)定义在R上的函数y=f(x)是减函数,且函数y=f(x-1)的图象关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2).则当1≤s≤4时,的取值范围是 ( )
A. B.
C. D.
【答题模板】
答案 D
解析 因函数y=f(x-1)的图象关于(1,0)成中心对称,所以该函数的图象向左平移一个单位后的解析式为y=f(x),即y=f(x)的图象关于(0,0)对称,所以y=f(x)是奇函数.又y=f(x)是R上的减函数,所以s2-2s≥t2-2t,令y=x2-2x=(x-1)2-1,
图象的对称轴为x=1,
当1≤s≤4时,要使s2-2s≥t2-2t,即s-1≥|t-1|,
当t≥1时,有s≥t≥1,所以≤≤1;
当t<1时,
即s-1≥1-t,即s+t≥2,
问题转化成了线性规划问题,画出由1≤s≤4,t<1,s+t≥2组成的不等式组的可行域.为可行域内的点到原点连线的斜率,易知-≤<1.综上可知选D.
【突破思维障碍】
当s,t位于对称轴x=1的两边时,如何由s2-2s≥t2-2t判断s,t之间的关系式,这时s,t与对称轴x=1的距离的远近决定着不等式s2-2s≥t2-2t成立与否,通过数形结合判断出关系式s-1≥1-t,从而得出s+t≥2,此时有一个隐含条件为t<1,再结合1≤s≤4及要求的式子的取值范围就能联想起线性规划,从而突破了难点.要画出s,t所在区域时,要结合的几何意义为点(s,t)和原点连线的斜率,确定s为横轴,t为纵轴.
【易错点剖析】
当得到不等式s2-2s≥t2-2t后,如果没有函数的思想将无法继续求解,得到二次函数后也容易只考虑s,t都在二次函数y=x2-2x的增区间[1,+∞)内,忽略考虑s,t在二次函数对称轴两边的情况,考虑了s,t在对称轴的两边,也容易漏掉隐含条件t<1及联想不起来线性规划.
1.掌握作函数图象的两种基本方法(描点法,图象变换法),在画函数图象时,要特别注意到用函数的性质(如单调性、奇偶性等)解决问题.
2.合理处理识图题与用图题
(1)识图.对于给定函数的图象,要能从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性.
(2)用图.函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具,要重视数形结合解题的思想方法,常用函数图象研究含参数的方程或不等式解集的情况.
(满分:75分)
一、选择题(每小题5分,共25分)
1.(2010·重庆)函数f(x)=的图象 ( )
A.关于原点对称 B.关于直线y=x对称
C.关于x轴对称 D.关于y轴对称
2.(2010·湖南)用min{a,b}表示a,b两数中的最小值.若函数f(x)=min{|x|,|x+t|}的图象关于直线x=-对称,则t的值为 ( )
A.-2 B.2
C.-1 D.1
3.(2011·北京海淀区模拟)在同一坐标系中画出函数y=logax,y=ax,y=x+a的图象,可能正确的是 ( )
4.(2011·深圳模拟)若函数y=f(x)的图象如图所示,则函数y=-f(x+1)的图象大致为
( )
5.设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为 ( )
A.1 B.-1 C. D.
题号
1
2
3
4
5
答案
二、填空题(每小题4分,共12分)
6.为了得到函数y=3×()x的图象,可以把函数y=()x的图象向________平移________个单位长度.
7.(2011·黄山月考)函数f(x)=的图象对称中心是________.
8.(2011·沈阳调研)如下图所示,向高为H的水瓶A、B、C、D同时以等速注水,注满为止.
(1)若水量V与水深h函数图象是下图的(a),则水瓶的形状是________;
(2)若水深h与注水时间t的函数图象是下图的(b),则水瓶的形状是________.
(3)若注水时间t与水深h的函数图象是下图的(c),则水瓶的形状是________;
(4)若水深h与注水时间t的函数的图象是图中的(d),则水瓶的形状是________.
三、解答题(共38分)
9.(12分)已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象;
(3)根据图象指出f(x)的单调递减区间;
(4)根据图象写出不等式f(x)>0的解集;
(5)求当x∈[1,5)时函数的值域.
10.(12分)(2011·三明模拟)当x∈(1,2)时,不等式(x-1)20).
(1)若g(x)=m有根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
答案 自主梳理
2.③奇偶性 单调性 周期性 3.(1)左 右 |a| 上 下 |a| (2)a>1 a>1 00的部分关于y轴的对称部分,
即得y=|x|的图象.
变式迁移1 解 定义域是{x|x∈R且x≠±1},且函数是偶函数.
又当x≥0且x≠1时,y=.
先作函数y=的图象,并将图象向右平移1个单位,得到函数y= (x≥0且x≠1)的图象(如图(a)所示).
又函数是偶函数,作关于y轴对称图象,
得y=的图象(如图(b)所示).
例2 解题导引 对于给定的函数的图象,要能从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性,注意图象与函数解析式中参数的关系.
(1)A[从f(x)、g(x)的图象可知它们分别为偶函数、奇函数,故f(x)·g(x)是奇函数,排除B.又x<0时,g(x)为增函数且为正值,f(x)也是增函数,故f(x)·g(x)为增函数,且正负取决于f(x)的正负,注意到x→(从小于0趋向于0),f(x)·g(x)→+∞,可排除C、D.](2)A[因为f(1-x)=f(-(x-1)),故y=f(1-x)的图象可以由y=f(x
)的图象按照如下变换得到:先将y=f(x)的图象关于y轴翻折,得y=f(-x)的图象,然后将y=f(-x)的图象向右平移一个单位,即得y=f(-x+1)的图象.]
变式迁移2 (1)A [考查函数y=2x与y=x2的图象可知:
当x<0时,方程2x-x2=0仅有一个零点,
且→-∞;
当x>0时,方程2x-x2=0有两个零点2和4,
且→+∞.]
(2)C [由图象知f(x)为奇函数,排除D;
又0,±,±π为方程f(x)=0的根,故选C.]
例3 解题导引 原方程重新整理为|x2-4x+3|=x+a,将两边分别设成一个函数并作出它们的图象,即求两图象至少有三个交点时a的取值范围.
方程的根的个数问题转化为函数图象交点个数问题,体现了《考纲》中函数与方程的重要思想方法.
解 原方程变形为|x2-4x+3|=x+a,于是,设y=|x2-4x+3|,y=x+a,在同一坐标系下分别作出它们的图象.如图.则当直线y=x+a过点(1,0)时a=-1;当直线y=x+a与抛物线y=-x2+4x-3相切时,由,得,x2-3x+a+3=0,
由Δ=9-4(3+a)=0,得a=-.
由图象知当a∈[-1,-]时方程至少有三个根.
变式迁移3 (1,)
解析 y=x2-|x|+a=
当其图象如图所示时满足题意.
由图知解得10,∴前两个图象不是给出的二次函数图象,又后两个图象的对称轴都在y轴右边,∴->0,∴a<0,又∵图象过原点,∴a2-1=0,∴a=-1.]
6.右 1
解析 ∵y=3×()x=()x-1,
∴y=()x向右平移1个单位便得到y=()x-1.
7.(-1,2)
解析 ∵f(x)===2-,
∴函数f(x)图象的对称中心为(-1,2).
8.(1)A (2)D (3)B (4)C
9.解 (1)∵f(4)=0,∴4|m-4|=0,即m=4.…………………………………………(2分)
(2)f(x)=x|x-4|
=………………………………………………(4分)
f(x)的图象如右图所示.
(3)由图可知,f(x)的减区间是[2,4].……………………………………………………(8分)
(4)由图象可知f(x)>0的解集为
{x|04}.………………………………………………………………………(10分)
(5)∵f(5)=5>4,
由图象知,函数在[1,5)上的值域为[0,5).……………………………………………(12分)
10.
解 设f1(x)=(x-1)2,
f2(x)=logax,
要使当x∈(1,2)时,不等式(x-1)21时,如图,要使在(1,2)上,f1(x)=(x-1)2的图象在f2(x)=logax的下方,只需f1(2)≤f2(2),
即(2-1)2≤loga2,loga2≥1,……………………………………………………………(10分)
∴10,∴g(x)=x+≥2=2e,
等号成立的条件是x=e.
故g(x)的值域是[2e,+∞),……………………………………………………………(4分)
因而只需m≥2e,则g(x)=m就有根.…………………………………………………(6分)
方法二 作出g(x)=x+的图象如图:
……………………………………………………………………………………………(4分)
可知若使g(x)=m有根,则只需m≥2e.………………………………………………(6分)
方法三 解方程由g(x)=m,得x2-mx+e2=0.
此方程有大于零的根,故……………………………………………(4分)
等价于,故m≥2e.…………………………………………………(6分)
(2)若g(x)-f(x)=0有两个相异的实根,即g(x)=f(x)中函数g(x)与f(x)的图象有两个不同的交点,
作出g(x)=x+ (x>0)的图象.
∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2.
其对称轴为x=e,开口向下,
最大值为m-1+e2.……………………………………………………………………(10分)
故当m-1+e2>2e,即m>-e2+2e+1时,
g(x)与f(x)有两个交点,
即g(x)-f(x)=0有两个相异实根.
∴m的取值范围是(-e2+2e+1,+∞).……………………………………………(14分)