2020年高考数学(理)二轮复习讲练测 专题22 几何体的表面积与体积的求解（测）（原卷版）

2020年高考数学(理)二轮复习讲练测 专题22 几何体的表面积与体积的求解（测）（原卷版）

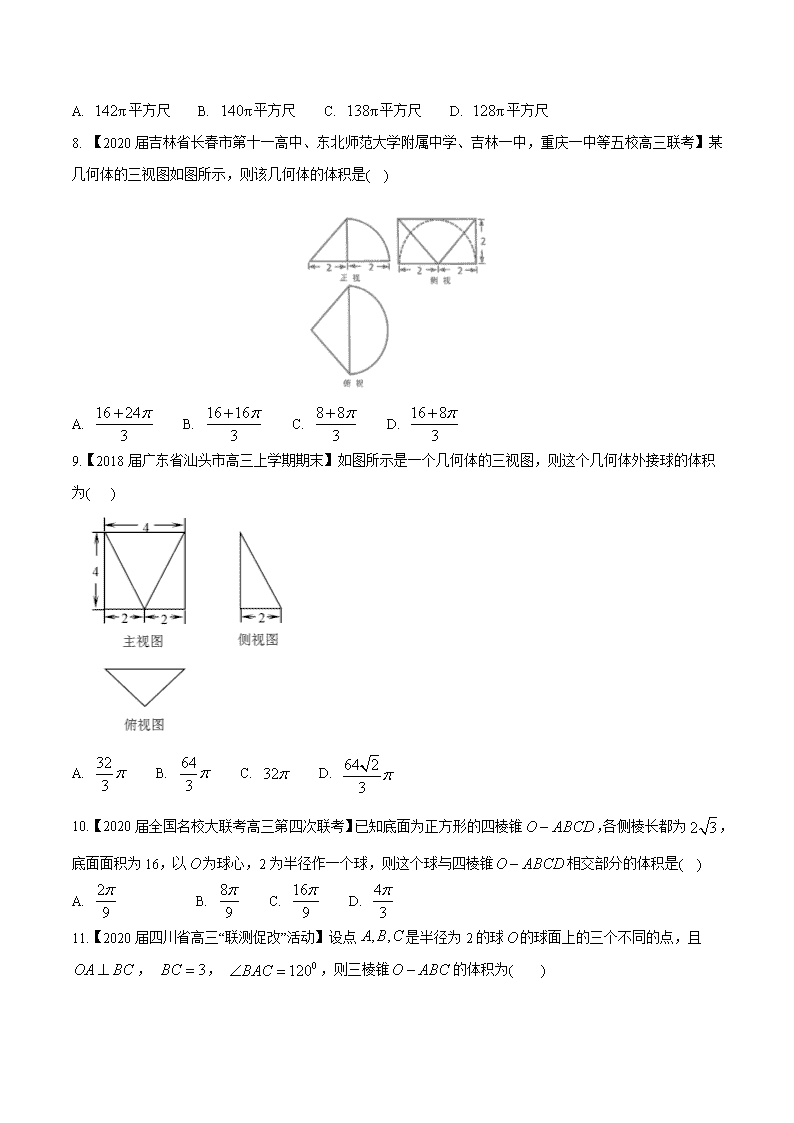
专题22 几何体的表面积与体积的求解 ‎【满分：100分 时间：90分钟】‎ （一） 选择题(12*5=60分)‎ ‎5．一空间几何体的三视图如下图所示，则该几何体的体积为( ) ‎ A．1 B．3 C．6 D．2‎ ‎2、【2020】届四川省成都实验中学高三月考】 某四棱锥的三视图如图所示，该四棱锥的表面积是( )‎ A. B. C. D. ‎ ‎3．如图所示，已知正三棱柱的所有棱长均为1，则三棱锥的体积为( )‎ A． ‎ B． ‎ C． D．‎ ‎4.【陕西省榆林市2020届高考模拟】一个正三棱柱的三视图如图所示，则正三棱柱的外接球的表面积是( )‎ A． B． C． D．‎ ‎5、【北京市海淀八校2020届高三模拟测试题】我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异”其中“幂”即是截面积，“势”是几何体的高，意思是两等高立方体，若在每一等高处的截面积都相等，则两立方体的体积相等，已知某不规则几何体与如图所示的几何体满足“幂势同”，则该不规则几何体的体积为　　‎ A． B． ‎ C． D．‎ ‎6、【河南省开封市2020届高三模拟】有四根长都为2的直铁条，若再选两根长都为的直铁条，使这六根铁条端点处相连能够焊接成一个对棱相等的三棱锥形的铁架，则此三棱锥体积的取值范围是 A． B． C． D．‎ ‎7.【2020届河北省承德市联校高三上学期期末】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有阳马，广五尺，褒七尺，高八尺，问积几何?”其意思为：“今有底面为矩形，一侧棱垂直于底面的四棱锥，它的底面长、宽分别为7尺和5尺，高为8尺，问它的体积是多少?”若以上的条件不变，则这个四棱锥的外接球的表面积为( )‎ A. 平方尺 B. 平方尺 C. 平方尺 D. 平方尺 ‎8. 【2020届吉林省长春市第十一高中、东北师范大学附属中学、吉林一中，重庆一中等五校高三联考】某几何体的三视图如图所示，则该几何体的体积是( )‎ A. B. C. D. ‎ ‎9.【2018届广东省汕头市高三上学期期末】如图所示是一个几何体的三视图，则这个几何体外接球的体积为( )‎ A. B. C. D. ‎ ‎10.【2020届全国名校大联考高三第四次联考】已知底面为正方形的四棱锥，各侧棱长都为，底面面积为16，以为球心，2为半径作一个球，则这个球与四棱锥相交部分的体积是( )‎ A. B. C. D. ‎ ‎11.【2020届四川省高三“联测促改”活动】设点是半径为2的球的球面上的三个不同的点，且， ， ，则三棱锥的体积为( )‎ A. B. C. D. ‎ ‎12．已知长方体的体积为6， 的正切值为，当的值最小时，长方体外接球的表面积为( )‎ A． B． C． D．‎ 二、填空题(4*5=20分)‎ ‎13. 三棱锥中，分别为的中点，记三棱锥的体积为，的体积为，则____________‎ ‎14.【2020届河北省石家庄市高三毕业班教学质量检测】直三棱柱的各顶点都在同一球面上，若， ， ， ，则此球的表面积等于__________．‎ ‎15.【2020届河南省商丘市高三月考】如图，在四棱锥中，四边形是边长为的正方形，且，已知四棱锥的表面积是，则它的体积为________．‎ ‎16.【福建省泉州市2020届高三质检】已知边长为2的菱形ABCD中，∠BAD＝60°，沿对角线BD折成二面角A－BD－C的大小为120°的四面体，则四面体的外接球的表面积为________．‎ 三、解答题(6*12=72分)‎ ‎17. 【河南省郑州市2020届高三月考】35．如图，直三棱柱的底面是边长为2的正三角形，分别是的中点．‎ ‎(１)证明：平面平面；‎ ‎(２)若直线与平面所成的角为，求三棱锥的体积．‎ ‎18．【2020届安徽省合肥市高三质量检测】如图，在多面体中， 是正方形， 平面， 平面， ，点为棱的中点. ‎ ‎(1)求证：平面平面；‎ ‎(2)若,求三棱锥的体积.‎ ‎19．如图，在四棱锥中，平面 平面，，， .‎ ‎(1)证明 ‎ ‎(2)设点在线段上，且，若的面积为，‎ 求四棱锥的体积 ‎20. 【山东省德州市2020届高三期末联考】如图，四棱锥中，平面平面，，，，，为线段上一点，，是线段的中点. ‎ ‎(1)证明：平面；‎ ‎(2)若，求四面体的体积.‎ ‎21．【黑龙江省哈尔滨市2020届高三上期末】如图，四边形是边长为的正方形，为等腰三角形，，平面平面，动点在棱上，无论点运动到何处时，总有.‎ ‎(1)试判断平面与平面是否垂直，并证明你的结论；‎ ‎(2)若点为中点，求三棱锥的体积.‎ ‎22．如图，在直三棱柱中，，是的中点，. ‎ ‎(1)求证：平面；‎ ‎(2)若异面直线和所成角的余弦值为，求四棱锥的体积.‎