2019学年高一数学上学期期初单元练习试题新人教 版新版
2019学年高一数学上学期期初单元练习试题
集合与函数
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
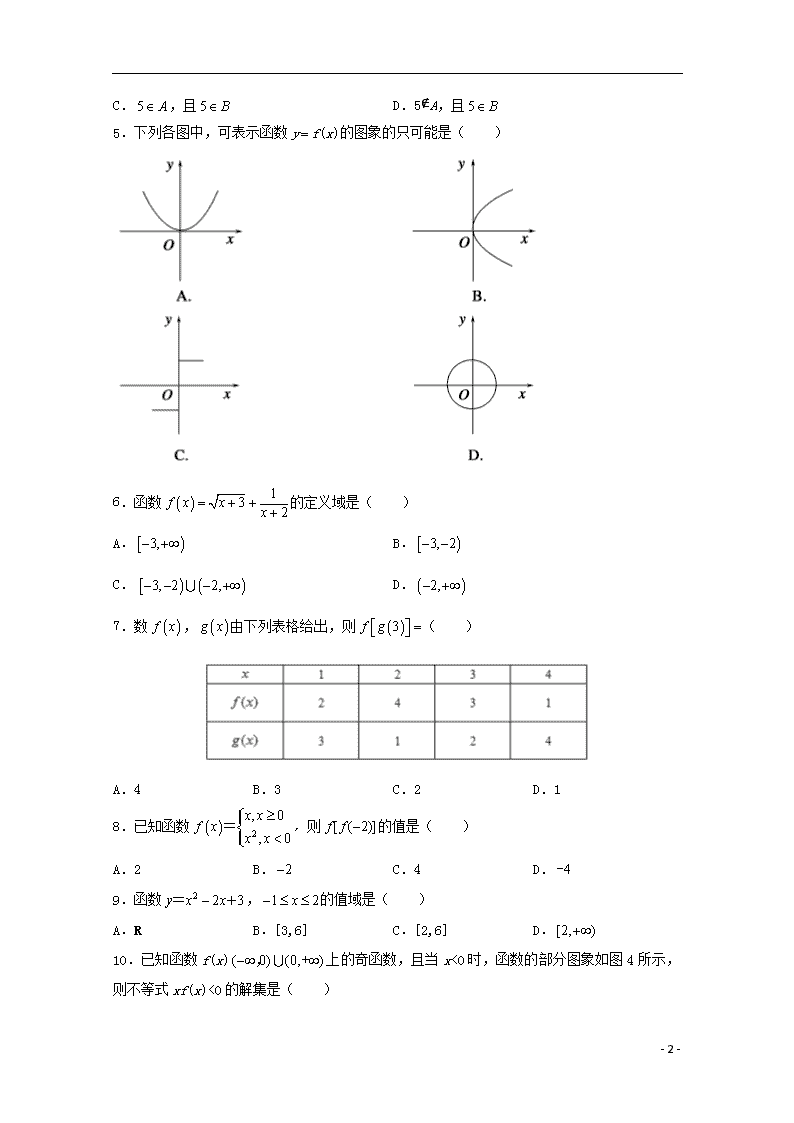
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,则集合( )
A.0 B. C. D.
2.设全集U=R,集合,集合,
则等于( )
A.{1,3,2,6} B.{(1,3),(2,6)}
C.M D.{3,6}
3.如图1所示,阴影部分表示的集合是( )
A. B.
C. D.
图1
4.设全集U{x|0
a},U=R.
- 12 -
(1)求A∪B,;
(2)若,求a的取值范围.
18.(12分)设A={x|x22(a1)xa21=0},,x∈Z}.
若A∩B=A,求a的取值范围.
- 12 -
19.(12分)已知函数f(x)=2xm,其中m为常数.
(1)求证:函数f(x)在R上是减函数;
(2)当函数f(x)是奇函数时,求实数m的值.
20.(12分)某公司生产的水笔上年度销售单价为元,年销售量为1亿支.本年度计划将销售单价调至元(含端点值),经调查,若销售单价调至x元,则本年度新增销售量y(亿支)与成反比,且当时,.
(1)求y与x的函数关系式;
(2)若每支水笔的成本价为元,则水笔销售单价调至多少时,本年度该公司的收益比上年度增加20%?
- 12 -
21.(12分)已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2,
(1)求函数f(x)和g(x);
(2)判断函数f(x)g(x)的奇偶性.
(3)求函数f(x)g(x)在上的最小值.
- 12 -
22.(12分)函数f(x)=是定义在上的奇函数,且.
(1)求f(x)的解析式;
(2)证明f(x)在上为增函数;
(3)解不等式f(t1)f(t)<0.
- 12 -
一、选择题
1.【答案】C
【解析】因为集合,,所以,故选C.
2.【答案】C
【解析】,N=R..故选C.
3.【答案】A
【解析】因为阴影部分既在集合中又在集合A中,
所以阴影部分为,故选A.
4.【答案】A
【解析】可借助Venn图(如图2)解决,数形结合.故选A.
图2
5.【答案】A
【解析】根据函数的概念知,只有“一对一”或“多对一”对应才能构成函数关系.
故选A.
6.【答案】C
【解析】由题可得:且,故选C.
7.【答案】A
【解析】由表可知,,故选A.
8.【答案】C
【解析】∵,而,∴.
- 12 -
又4>0,∴.故选C.
9.【答案】C
【解析】画出函数,的图象,如图3所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6],所以值域是[2,6].故选C.
10.【答案】D
【解析】xf(x)<0⇔x与f(x)异号,由函数图象及奇偶性易得结论.故选D.
11.【答案】B
【解析】∵f(x)是偶函数,∴f(x)的图象关于y轴对称.
∴f(x)在上是减函数,且最大值为6.故选B.
12.【答案】C
【解析】∵对任意(x1≠x2),都有,
∴对任意,若x18}.∴={x|10.∴f(x1)>f(x2)
- 12 -
∴函数f(x)在R上是减函数.
(2)∵函数f(x)是奇函数,
∴对任意x∈R,有f(x)=f(x).
∴2xm=(2xm).∴m=0.
20.【答案】(1)y=;(2)元.
【解析】(1)设y=,由,,得,
所以y=.
(2)依题意,,
解得x=或x=(舍去),所以水笔销售单价应调至元.
21.【答案】(1)f(x)=x,g(x)=;(2)奇函数;(3).
【解析】(1)设,g(x)=,其中k1k2≠0.
∵f(1)=1,g(1)=2,∴,.
∴k1=1,k2=2.∴f(x)=x,g(x)=.
(2)设h(x)=f(x)g(x),则,
∴函数h(x)的定义域是.
∵h(x)=x==h(x),
∴函数h(x)是奇函数,即函数f(x)g(x)是奇函数.
(3)由(2)知,设x1,x2是上的任意两个实数,且x10.
∴h(x1)>h(x2).
- 12 -
∴函数h(x)在上是减函数,函数h(x)在上的最小值是.
即函数f(x)g(x)在上的最小值是.
22.【答案】(1)f(x)=;(2)见解析;(3).
【解析】(1)由题意得,
解得,所以f(x)=.
(2)证明:任取两数x1,x2,且10,
所以f(x1)f(x2)<0,故f(x)在上是增函数.
(3)因为f(x)是奇函数,所以由f(t1)+f(t)<0,得f(t1)
查看更多