山东省泰安市2020届高三第二轮复习质量检测（二模）数学试题

山东省泰安市2020届高三第二轮复习质量检测（二模）数学试题

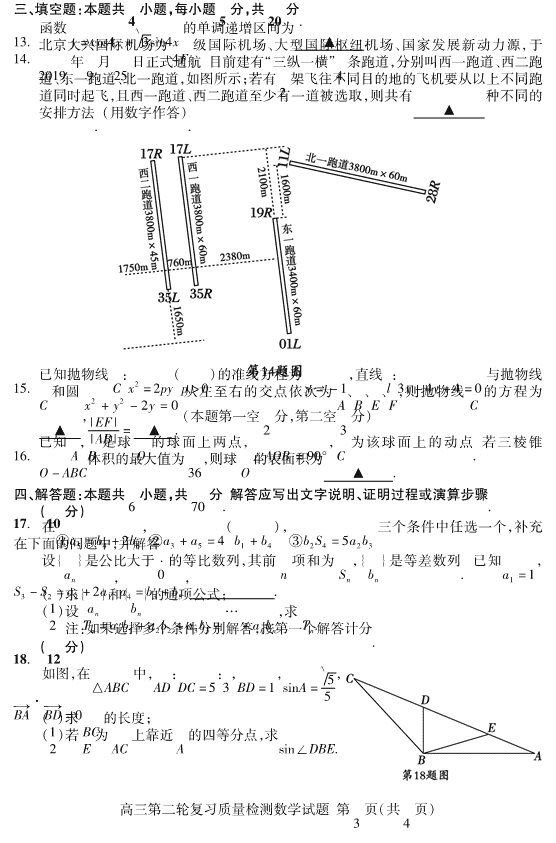
书 试卷类型：Ａ 高三第二轮复习质量检测 数　 学　 试　 题 ２０２０ ５ 注意事项： １． 答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。 ２． 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。 如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡 上。写在本试卷上无效。 ３． 考试结束后，将本试卷和答题卡一并交回。 一、单项选择题：本题共 ８ 小题，每小题 ５ 分，共 ４０ 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． １． 若集合 Ａ ＝｛ｘ ｜（ｘ ＋ １）（ｘ － ２）＜ ０｝，Ｂ ＝｛ｘ ｜ ｌｎｘ ＞ ０｝，则 Ａ∩Ｂ ＝ Ａ． ｛ｘ ｜１ ＜ ｘ ＜ ２｝　 　 　 　 　 　 　 　 　 Ｂ． ｛ｘ ｜ － １ ＜ ｘ ＜ １｝ Ｃ． ｛ｘ ｜ － １ ＜ ｘ ＜ ２｝ Ｄ． ｛ｘ ｜ － ２ ＜ ｘ ＜ １｝ ２． 已知复数 ｚ ＝ １ － ｉ２ ＋ ｉ，ｉ为虚数单位，则 －ｚ ＝ Ａ． １５ － ３ ５ ｉ Ｂ． １５ ＋ ３ ５ ｉ Ｃ． － １５ － ３ ５ ｉ Ｄ． － １５ ＋ ３ ５ ｉ ３． 已知直线 ｌ过点 Ｐ（３，０），圆 Ｃ：ｘ２ ＋ ｙ２ － ４ｘ ＝ ０，则 Ａ． ｌ与 Ｃ相交 Ｂ． ｌ与 Ｃ相切 Ｃ． ｌ与 Ｃ相离 Ｄ． ｌ与 Ｃ的位置关系不确定 ４． 已知（１ － ｐｘ）ｎ ＝ ｂ０ ＋ ｂ１ｘ ＋ ｂ２ｘ ２ ＋… ＋ ｂｎｘ ｎ，若 ｂ１ ＝ － ３，ｂ２ ＝ ４，则 ｐ ＝ Ａ． １　 　 　 　 　 　 Ｂ． １２ 　 　 　 　 　 　 Ｃ． １ ３ 　 　 　 　 　 　 Ｄ． １ ４ ５． 中国古代“五行”学说认为：物质分“金、木、水、火、土”五种属性，并认为：“金生水、水 生木、木生火、火生土、土生金”；从五种不同属性的物质中随机抽取 ２ 种，则抽到的两 种物质不相生的概率为 Ａ． １５ Ｂ． １４ Ｃ． １２ Ｄ． １３ ６． 命题 ｐ： ｘ∈［－ ２，１］，ｘ２ ＋ ｘ －ｍ≤０ 成立的充要条件是 Ａ． ｍ≥０ Ｂ． ｍ≥ － １４ Ｃ． － １４ ≤ｍ≤２ Ｄ． ｍ≥２ ７． 在直角三角形 ＡＢＣ中，∠ＡＣＢ ＝ π２ ，ＡＣ ＝ ＢＣ ＝ ２，点 Ｐ是斜边 ＡＢ 上一点，且 ＢＰ ＝ ２ＰＡ， 则 →ＣＰ·→ＣＡ ＋ →ＣＰ·→ＣＢ ＝ Ａ． － ４ Ｂ． － ２ Ｃ． ２ Ｄ． ４ 高三第二轮复习质量检测数学试题 第 １ 页（共 ４ 页） ８． 已知函数 ｆ（ｘ）＝（ｘ － １）ｅｘ － ａ２ ｅ ２ｘ ＋ ａｘ只有一个极值点，则实数 ａ的取值范围是 Ａ． ａ≤０ 或 ａ≥ １２ Ｂ． ａ≤０ 或 ａ≥ １３ Ｃ． ａ≤０ Ｄ． ａ≥０ 或 ａ≤ － １３ 二、多项选择题：本题共 ４ 小题，每小题 ５ 分，共 ２０ 分．在每小题给出的选项中，有多项符 合题目要求．全部选对的得 ５ 分，部分选对的得 ３ 分，有选错的得 ０ 分． ９． “杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广，发明了“三系 法”籼型杂交水稻，成功研究出“两系法”杂交水稻，创建了超级杂交稻技术体系，为我 国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献；某杂交水稻种植研究所 调查某地水稻的株高，得出株高（单位：ｃｍ）服从正态分布，其密度曲线函数为 ｆ（ｘ）＝ １ １０ ２槡 π ｅ － （ｘ － １００）２ ２００ ，ｘ∈（－ ∞，＋ ∞），则下列说法正确的是 Ａ． 该地水稻的平均株高为 １００ｃｍ Ｂ． 该地水稻株高的方差为 １０ Ｃ． 随机测量一株水稻，其株高在 １２０ｃｍ以上的概率比株高在 ７０ｃｍ以下的概率大 Ｄ． 随机测量一株水稻，其株高在（８０，９０）和在（１００，１１０）（单位：ｃｍ）的概率一样大 １０． 如图，正方体 ＡＢＣＤ － Ａ１Ｂ１Ｃ１Ｄ１ 的棱长为 ２，线段 Ｂ１Ｄ１ 上有两个动点 Ｍ，Ｎ，且 ＭＮ ＝ １，则下列结论正 确的是 Ａ． ＡＣ⊥ＢＭ Ｂ． ＭＮ∥平面 ＡＢＣＤ Ｃ． 三棱锥 Ａ － ＢＭＮ的体积为定值 Ｄ． △ＡＭＮ的面积与△ＢＭＮ的面积相等 １１． 已知双曲线 ｘ ２ ａ２ － ｙ ２ ｂ２ ＝ １（ａ ＞ ０，ｂ ＞ ０）的一条渐近线 方程为 ｘ － ２ｙ ＝ ０，双曲线的左焦点在直线 ｘ ＋ ｙ 槡＋ ５ ＝ ０上，Ａ、Ｂ 分别是双曲线的左、右顶点，点 Ｐ为双曲线右支上位于第一象限的动点，ＰＡ，ＰＢ 的斜率分别为 ｋ１，ｋ２，则 ｋ１ ＋ ｋ２ 的取 值可能为 Ａ． ３４ Ｂ． １ Ｃ． ４３ Ｄ． ２ １２． 在平面直角坐标系 ｘＯｙ 中，如图放置的边长为 ２ 的正方形 ＡＢＣＤ沿 ｘ 轴滚动（无滑动滚动），点 Ｄ 恰好经过坐标原点，设顶点 Ｂ（ｘ，ｙ）的轨迹方程是 ｙ ＝ ｆ（ｘ），则对函数 ｙ ＝ ｆ（ｘ）的判断正确的是 Ａ． 函数 ｇ（ｘ）＝ ｆ（ｘ） 槡－ ２ ２在［－ ３，９］上有两个 零点 Ｂ． 函数 ｙ ＝ ｆ（ｘ）是偶函数 Ｃ． 函数 ｙ ＝ ｆ（ｘ）在［－ ８，－ ６］上单调递增 Ｄ． 对任意的 ｘ∈Ｒ，都有 ｆ（ｘ ＋ ４）＝ － １ｆ（ｘ） 高三第二轮复习质量检测数学试题 第 ２ 页（共 ４ 页） 三、填空题：本题共 ４ 小题，每小题 ５ 分，共 ２０ 分． １３． 函数 ｙ ＝ ｃｏｓ４ｘ 槡＋ ３ｓｉｎ４ｘ的单调递增区间为　 　 ▲　 　 ． １４． 北京大兴国际机场为 ４Ｆ 级国际机场、大型国际枢纽机场、国家发展新动力源，于 ２０１９ 年 ９ 月 ２５ 日正式通航．目前建有“三纵一横”４ 条跑道，分别叫西一跑道、西二跑 道、东一跑道、北一跑道，如图所示；若有 ２ 架飞往不同目的地的飞机要从以上不同跑 道同时起飞，且西一跑道、西二跑道至少有一道被选取，则共有　 　 ▲　 　 种不同的 安排方法．（用数字作答）． １５． 已知抛物线 Ｃ：ｘ２ ＝ ２ｐｙ（ｐ ＞ ０）的准线方程为 ｙ ＝ － １，直线 ｌ：３ｘ － ４ｙ ＋ ４ ＝ ０ 与抛物线 Ｃ和圆 ｘ２ ＋ ｙ２ － ２ｙ ＝ ０ 从左至右的交点依次为 Ａ、Ｂ、Ｅ、Ｆ，则抛物线 Ｃ 的方程为 　 ▲　 ，｜ＥＦ ｜｜ＡＢ ｜ ＝ 　 ▲　 ．（本题第一空 ２ 分，第二空 ３ 分） １６． 已知 Ａ，Ｂ 是球 Ｏ 的球面上两点，∠ＡＯＢ ＝ ９０°，Ｃ 为该球面上的动点． 若三棱锥 Ｏ － ＡＢＣ体积的最大值为 ３６，则球 Ｏ的表面积为　 　 ▲　 　 ． 四、解答题：本题共 ６ 小题，共 ７０ 分．解答应写出文字说明、证明过程或演算步骤． １７． （１０ 分） 在①ａ５ ＝ ｂ４ ＋ ２ｂ６，②ａ３ ＋ ａ５ ＝ ４（ｂ１ ＋ ｂ４），③ｂ２Ｓ４ ＝ ５ａ２ｂ３ 三个条件中任选一个，补充 在下面的问题中，并解答． 设｛ａｎ｝是公比大于 ０ 的等比数列，其前 ｎ 项和为 Ｓｎ，｛ｂｎ｝是等差数列． 已知ａ１ ＝ １， Ｓ３ － Ｓ２ ＝ ａ２ ＋ ２ａ１，ａ４ ＝ ｂ３ ＋ ｂ５， ． （１）求｛ａｎ｝和｛ｂｎ｝的通项公式； （２）设 Ｔｎ ＝ ａ１ｂ１ ＋ ａ２ｂ２ ＋ ａ３ｂ３ ＋… ＋ ａｎｂｎ，求 Ｔｎ． 注：如果选择多个条件分别解答，按第一个解答计分． １８． （１２ 分） 如图，在△ＡＢＣ中，ＡＤ：ＤＣ ＝ ５：３，ＢＤ ＝ １，ｓｉｎＡ ＝槡５５ ， →ＢＡ· →ＢＤ ＝ ０ （１）求 ＢＣ的长度； （２）若 Ｅ为 ＡＣ上靠近 Ａ的四等分点，求ｓｉｎ∠ＤＢＥ． 高三第二轮复习质量检测数学试题 第 ３ 页（共 ４ 页） １９． （１２ 分） 如图所示，在直三棱柱 ＡＢＣ － Ａ１Ｂ１Ｃ１ 中，ＡＢ⊥ＡＣ，侧面 ＡＢＢ１Ａ１ 是正方形，ＡＢ ＝ ３，ＡＣ 槡＝ ３ ６． （１）证明：平面 ＡＢ１Ｃ１⊥平面 Ａ１ＢＣ１； （２）若 →ＡＭ ＝ １６ →ＡＣ，求二面角 Ｍ － ＢＣ１ － Ａ１ 的大小． ２０． （１２ 分） 某人玩掷正方体骰子走跳棋的游戏，已知骰子每面朝上 的概率都是 １ ６ ，棋盘上标有第 ０ 站，第 １ 站，第 ２ 站，……，第 １００ 站。一枚棋子开始在第 ０ 站，选手每掷一次骰子，棋子向前跳动一次，若掷出朝上的 点数为 １ 或 ２，棋子向前跳两站；若掷出其余点数，则棋子向前跳一站，直到跳到第 ９９ 站 或第 １００ 站时，游戏结束；设游戏过程中棋子出现在第 ｎ站的概率为 Ｐｎ． （１）当游戏开始时，若抛掷均匀骰子 ３ 次后，求棋子所走站数之和 Ｘ的分布列与数学 期望； （２）证明：Ｐｎ ＋ １ － Ｐｎ ＝ － １ ３ （Ｐｎ － Ｐｎ － １）（１≤ｎ≤９８）； （３）若最终棋子落在第 ９９ 站，则记选手落败，若最终棋子落在第 １００ 站，则记选手获 胜，请分析这个游戏是否公平． ２１． （１２ 分） 已知椭圆 Ｃ：ｘ ２ ａ２ ＋ ｙ ２ ｂ２ ＝ １（ａ ＞ ｂ ＞ ０）的离心率 ｅ 满足 ２ｅ２ 槡－ ３ ２ｅ ＋ ２ ＝ ０，以坐标原点为圆心，椭圆 Ｃ 的长轴长为半径 的圆与直线 ２ｘ － ｙ 槡＋ ４ ５ ＝ ０ 相切． （１）求椭圆 Ｃ的方程； （２）过点 Ｐ（０，１）的动直线 ｌ（直线 ｌ 的斜率存在）与椭圆 Ｃ 相交于 Ａ，Ｂ两点，问在 ｙ轴上是否存在与点 Ｐ 不同的定点 Ｑ，使得 ｜ＱＡ ｜｜ＱＢ ｜ ＝ Ｓ△ＡＰＱ Ｓ△ＢＰＱ 恒成立？ 若存在，求出定点 Ｑ的坐标；若不存在，请说明理由． ２２． （１２ 分） 已知函数 ｆ（ｘ）＝（ｘ ＋ １）ｅ － ｘ ＋（ｘ － １）ｅｘ，ｘ≥０． （１）证明：０≤ｆ（ｘ）≤ １ ｘ ＋ １ ＋ ｘ( )－ １ ｅｘ； （２）若 ｇ（ｘ）＝ ａｘ ＋ ｘ ３ ２ ＋ ｘ ＋ ２ｘｃｏｓ( )ｘ ｅｘ，当 ｘ∈［０，１］，ｆ（ｘ）≥ｇ（ｘ）恒成立，求实数 ａ 的取值范围． 高三第二轮复习质量检测数学试题 第 ４ 页（共 ４ 页） 高三第二轮复习质量检测 数学参考答案及评分标准 ２０２０ ５ 一、单项选择题： 题　 号 １ ２ ３ ４ ５ ６ ７ ８ 答　 案 Ａ Ｂ Ａ Ｃ Ｃ Ｂ Ｄ Ａ 二、多项选择题： 题　 号 ９ １０ １１ １２ 答　 案 ＡＣ ＡＢＣ ＣＤ ＡＢＤ 三、填空题： １３． ｋπ２ － π ６ ， ｋπ ２ ＋ π[ ]１２ （ｋ∈Ｚ）　 　 　 １４． １０　 　 　 １５． ｘ２ ＝ ４ｙ，１６ １６． １４４π 四、解答题： １７． （１０ 分） 解：解：方案一：选条件①： （１）设等比数列｛ａｎ｝的公比为 ｑ． ∵ ａ１ ＝ １，Ｓ３ － Ｓ２ ＝ ａ２ ＋ ２ａ１ ∴ ｑ２ － ｑ － ２ ＝ ０ 解得 ｑ ＝ ２ 或 ｑ ＝ － １ ∵ ｑ ＞ ０ ∴ ｑ ＝ ２ ∴ ａｎ ＝ ２ ｎ － １ ． ２ 分!!!!!!!!!!!!!!!!!!!!!!!!! 设等差数列｛ｂｎ｝的公差为 ｄ ∵ ａ４ ＝ ｂ３ ＋ ｂ５，ａ５ ＝ ｂ４ ＋ ２ｂ６ ∴ ｂ１ ＋ ３ｄ ＝ ４ ３ｂ１ ＋ １３ｄ{ ＝ １６ 解得 ｂ１ ＝ １ ｄ{ ＝ １ ∴ ｂｎ ＝ ｎ． ∴ ａｎ ＝ ２ ｎ － １，ｂｎ ＝ ｎ ５ 分!!!!!!!!!!!!!!!!!!!!!! （２）由（１）可知：ａｎ ＝ ２ ｎ － １，ｂｎ ＝ ｎ， ∴ Ｔｎ ＝ ａ１ｂ１ ＋ ａ２ｂ２ ＋… ＋ ａｎｂｎ ＝ １ × ２０ ＋ ２ × ２１ ＋… ＋（ｎ － １）× ２ｎ － ２ ＋ ｎ × ２ｎ － １ ∴ ２Ｔｎ ＝ １ × ２ １ ＋ ２ × ２２ ＋… ＋（ｎ － １）× ２ｎ － １ ＋ ｎ × ２ｎ ７ 分!!!!!!!! ∴ － Ｔｎ ＝ １ ＋ ２ １ ＋ ２２ ＋… ＋ ２ｎ － １ － ｎ × ２ｎ 高三第二轮复习质量检测数学试题参考答案 第 １ 页（共 ７ 页） ＝ １ － ２ ｎ １ － ２ － ｎ × ２ ｎ ＝ ２ｎ － １ － ｎ × ２ｎ ９ 分!!!!!!!!!!!!! ∴ Ｔｎ ＝（ｎ － １）·２ ｎ ＋ １． １０ 分!!!!!!!!!!!!!!!!!!!! 方案二：选条件②： （１）设等比数列｛ａｎ｝的公比为 ｑ． ∵ ａ１ ＝ １，Ｓ３ － Ｓ２ ＝ ａ２ ＋ ２ａ１ ∴ ｑ２ － ｑ － ２ ＝ ０ 解得 ｑ ＝ ２ 或 ｑ ＝ － １ ∵ ｑ ＞ ０ ∴ ｑ ＝ ２ ∴ ａｎ ＝ ２ ｎ － １ ． ２ 分!!!!!!!!!!!!!!!!!!!!!!!!! 设等差数列｛ｂｎ｝的公差为 ｄ ∵ ａ４ ＝ ｂ３ ＋ ｂ５，ａ３ ＋ ａ５ ＝ ４（ｂ１ ＋ ｂ４） ∴ ｂ１ ＋ ３ｄ ＝ ４ ２ｂ１ ＋ ３ｄ{ ＝ ５ 解得 ｂ１ ＝ １ ｄ{ ＝ １ ∴ ｂｎ ＝ ｎ． ∴ ａｎ ＝ ２ ｎ － １，ｂｎ ＝ ｎ． ５ 分!!!!!!!!!!!!!!!!!!!!!! （２）同方案一（２）． 方案三：选条件③： （１）设等比数列｛ａｎ｝的公比为 ｑ． ∵ ａ１ ＝ １，Ｓ３ － Ｓ２ ＝ ａ２ ＋ ２ａ１ ∴ ｑ２ － ｑ － ２ ＝ ０ 解得 ｑ ＝ ２ 或 ｑ ＝ － １ ∵ ｑ ＞ ０ ∴ ｑ ＝ ２ ∴ ａｎ ＝ ２ ｎ － １ ． ２ 分!!!!!!!!!!!!!!!!!!!!!!!!! 设等差数列｛ｂｎ｝的公差为 ｄ ∵ ａ４ ＝ ｂ３ ＋ ｂ５，ｂ２Ｓ４ ＝ ５ａ２ｂ３ ∴ ｂ１ ＋ ３ｄ ＝ ４ ｂ１ － ｄ{ ＝ ０ 解得 ｂ１ ＝ １ ｄ{ ＝ １ ∴ ｂｎ ＝ ｎ ∴ ａｎ ＝ ２ ｎ － １，ｂｎ ＝ ｎ． ５ 分!!!!!!!!!!!!!!!!!!!!!! （２）同方案一（２）． １８． （１２ 分） 解：（１）∵ →ＢＡ· →ＢＤ ＝ ０ ∴ ＢＡ⊥ＢＤ 在△ＡＢＤ中，ＢＤ ＝ １，ｓｉｎＡ ＝槡５５ 高三第二轮复习质量检测数学试题参考答案 第 ２ 页（共 ７ 页） ∴ ＡＤ 槡＝ ５，ｃｏｓ∠ＡＤＢ ＝槡 ５ ５ 又∵ ＡＤ ∶ ＤＣ ＝ ５ ∶ ３ ∴ ＤＣ ＝ 槡３ ５５ ３ 分!!!!!!!!!!!!!!!!!!!!!!!!! 在△ＢＣＤ中，ｃｏｓ∠ＢＤＣ ＝ －槡５５ ∴ ＢＣ２ ＝ ＣＤ２ ＋ ＢＤ２ － ２ × ＣＤ × ＢＤ × ｃｏｓ∠ＢＤＣ ＝ ９５ ＋ １ － ２ × 槡３ ５ ５ × １ ×（－ 槡５ ５ ） ＝ ４ ∴ ＢＣ ＝ ２ ６ 分!!!!!!!!!!!!!!!!!!!!!!!!!! （２）由（１）知，ＡＢ ＝ ２，ＡＥ ＝ １４ ＡＣ ＝ ２ ５槡５，ｃｏｓＡ ＝ 槡２ ５ ５ 在△ＡＢＥ中 ＢＥ２ ＝ ＡＢ２ ＋ ＡＥ２ － ２ × ＡＢ × ＡＥ × ｃｏｓＡ ＝ ４ ＋ ４５ － ２ × ２ × 槡２ ５ ５ × 槡２ ５ ５ ＝ ８５ ∴ ＢＥ ＝ 槡２ １０ ５ ９ 分!!!!!!!!!!!!!!!!!!!!!!!! 在△ＢＤＥ中，ＤＥ ＝ 槡３ ５５ ，ｓｉｎ∠ＢＤＥ ＝ 槡２ ５ ５ ∵ ＤＥ ｓｉｎ∠ＤＢＥ ＝ ＢＥ ｓｉｎ∠ＢＤＥ ∴ ｓｉｎ∠ＤＢＥ ＝ ＤＥ × ｓｉｎ∠ＢＤＥＢＥ ＝ 槡３ １０ １０ １２ 分!!!!!!!!!!!!!! １９． （１２ 分） 解：（１）证明：∵ 三棱柱 ＡＢＣ － Ａ１Ｂ１Ｃ１ 为直三棱柱 ∴ ＡＡ１⊥Ａ１Ｃ１ ∵ ＡＢ⊥ＡＣ ∴ Ａ１Ｃ１⊥Ａ１Ｂ１ ２ 分!!!!!!!!!!!!!!!!!!!!!!!! 又 ＡＡ１，Ａ１Ｂ１ 平面 ＡＢＢ１Ａ１，ＡＡ１∩Ａ１Ｂ１ ＝ Ａ１ ∴ Ａ１Ｃ１⊥平面 ＡＢＢ１Ａ１ 又 ＡＢ１ 平面 ＡＢＢ１Ａ１， ∴ ＡＢ１⊥Ａ１Ｃ１ 又侧面 ＡＢＢ１Ａ１ 为正方形 ∴ Ａ１Ｂ⊥ＡＢ１ ４ 分!!!!!!!!!!!!!!!!!!!!!!!!! 又 Ａ１Ｃ１，Ａ１Ｂ 平面 Ａ１ＢＣ１ Ａ１Ｂ∩Ａ１Ｃ１ ＝ Ａ１ ∴ ＡＢ１⊥平面 Ａ１ＢＣ１ 高三第二轮复习质量检测数学试题参考答案 第 ３ 页（共 ７ 页） 又 ＡＢ１ 平面 ＡＢ１Ｃ１ ∴ 平面 ＡＢ１Ｃ１⊥平面 Ａ１ＢＣ１ ６ 分!!!!!!!!!!!!!!!!!! （２）如图，以 Ａ１ 为坐标原点，建立空间直角坐标系 Ｏ － ｘｙｚ，则 Ａ（０，０，３），Ｂ（０，３，３），Ｂ１（０，３，０），Ｃ１（ 槡３ ６，０，０）， Ｃ（槡３ ６，０，３） ∴ →ＡＣ ＝（槡３ ６，０，０），ＡＢ → １ ＝（０，３，－ ３）， →ＡＢ ＝（０，３，０），ＢＣ→ １ ＝（槡３ ６，－ ３，－ ３） ∴ →ＭＢ ＝ →ＡＢ － →ＡＭ ＝ →ＡＢ － １６ →ＡＣ ＝（－槡６２ ，３，０） ８ 分!!!!!!!!!!!!!!!!!!!!! 设平面 ＭＢＣ１ 的一个法向量为 ｎ ＝（ｘ，ｙ，１），则 ｎ· →ＭＢ ＝ ０ ｎ·ＢＣ→ １ { ＝ ０ 解得 ｘ ＝槡６５ ，ｙ ＝ １ ５ ∴ ｎ ＝（槡６５ ， １ ５ ，１） １０ 分!!!!!!!!!!!!!!!!!!!!!! 又ＡＢ→ １是平面 Ａ１ＢＣ１ 的一个法向量 ∴ ｃｏｓ〈ｎ，ＡＢ→ １〉＝ ３ ５ － ３ ３２ 槡２５ 槡× １８ ＝ － １２ ∴ 〈ｎ，ＡＢ→ １〉＝ ２π ３ ∴ 二面角 Ｍ － ＢＣ１ － Ａ１ 的大小为 π ３ ． １２ 分!!!!!!!!!!!!!! ２０． （１２ 分） 解：（１）随机变量 Ｘ的所有可能取值为 ３，４，５，６， Ｐ（Ｘ ＝ ３）＝ ( )２３ ３ ＝ ８２７，Ｐ（Ｘ ＝ ４）＝ Ｃ １ ３ × ( )２３ ２ × ( )１３ ＝ ４９ Ｐ（Ｘ ＝ ５）＝ Ｃ２３ × ( )２３ × ( )１３ ２ ＝ ２９ ，Ｐ（Ｘ ＝ ６）＝ ( )１３ ３ ＝ １２７ ２ 分!!!!!! 所以，随机变量 Ｘ的分布列为 Ｘ ３ ４ ５ ６ Ｐ ８ ２７ ４ ９ ２ ９ １ ２７ ∴ Ｅ（Ｘ）＝ ３ × ８２７ ＋ ４ × ４ ９ ＋ ５ × ２ ９ ＋ ６ × １ ２７ ＝ ４ ４ 分!!!!!!!!!!! （２）由题意知，当 １≤ｎ≤９８ 时，棋子要到第（ｎ ＋ １）站，有两种情况： 高三第二轮复习质量检测数学试题参考答案 第 ４ 页（共 ７ 页） ①由第 ｎ站跳 １ 站得到，其概率为 ２３ Ｐｎ； ②由第（ｎ － １）站跳 ２ 站得到，其概率为 １３ Ｐｎ － １ ６ 分!!!!!!!!!!! ∴ Ｐｎ ＋ １ ＝ ２ ３ Ｐｎ ＋ １ ３ Ｐｎ － １ ∴ Ｐｎ ＋ １ － Ｐｎ ＝ ２ ３ Ｐｎ ＋ １ ３ Ｐｎ － １ － Ｐｎ ＝ － １ ３ （Ｐｎ － Ｐｎ － １） ∴ Ｐｎ ＋ １ － Ｐｎ ＝ － １ ３ （Ｐｎ － Ｐｎ － １）（１≤ｎ≤９８） ８ 分!!!!!!!!!!!! （３）由（２）知，当棋子落到第 ９９ 站游戏结束的概率为 Ｐ９９ ＝ ２ ３ Ｐ９８ ＋ １ ３ Ｐ９７， 当棋子落到第 １００ 站游戏结束的概率为 Ｐ１００ ＝ １ ３ Ｐ９８， １０ 分!!!!!!! ∵ Ｐ１００ ＜ Ｐ９９， ∴ 最终棋子落在第 ９９ 站的概率大于落在第 １００ 站的概率 ∴ 游戏不公平． １２ 分!!!!!!!!!!!!!!!!!!!!!!! ２１． （１２ 分） 解：（１）由题意知 ２ａ ＝ 槡０ － ０ ＋ ４ ５ 槡４ ＋ １ ， ∴ ａ ＝ ２ 由 ２ｅ２ 槡－ ３ ２ｅ ＋ ２ ＝ ０ 解得 ｅ ＝槡２２ 或 ｅ 槡＝ ２（舍） ２ 分!!!!!!!!!!!!!!!!!!!! ∴ ｂ 槡＝ ２ ∴ 椭圆 Ｃ的方程为ｘ ２ ４ ＋ ｙ２ ２ ＝ １． ４ 分!!!!!!!!!!!!!!!!! （２）存在 ５ 分!!!!!!!!!!!!!!!!!!!!!!!!!!!! 假设 ｙ轴上存在与点 Ｐ不同的定点 Ｑ，使得 ｜ＱＡ ｜｜ＱＢ ｜ ＝ Ｓ△ＡＰＱ Ｓ△ＢＰＱ 恒成立 设 Ｑ（０，ｍ）（ｍ≠１），Ａ（ｘ１，ｙ１），Ｂ（ｘ２，ｙ２），直线 ｌ的方程为 ｙ ＝ ｋｘ ＋ １ 由 ｘ２ ４ ＋ ｙ２ ２ ＝ １ ｙ ＝ ｋｘ{ ＋ １ ，可得 （２ｋ２ ＋ １）ｘ２ ＋ ４ｋｘ － ２ ＝ ０ ∴ ｘ１ ＋ ｘ２ ＝ － ４ｋ ２ｋ２ ＋ １ ，ｘ１ｘ２ ＝ － ２ ２ｋ２ ＋ １ Δ ＝ １６ｋ２ ＋ ８（２ｋ２ ＋ １）＝ ３２ｋ２ ＋ ８ ＞ ０ ７ 分!!!!! Ｓ△ＡＰＱ Ｓ△ＢＰＱ ＝ １ ２ ｜ＱＰ ｜ ｜ＱＡ ｜ ｓｉｎ∠ＰＱＡ １ ２ ｜ＱＰ ｜ ｜ＱＢ ｜ ｓｉｎ∠ＰＱＢ ＝ ｜ＱＡ ｜ ｓｉｎ∠ＰＱＡ｜ＱＢ ｜ ｓｉｎ∠ＰＱＢ ８ 分!!!!!!!!!! 高三第二轮复习质量检测数学试题参考答案 第 ５ 页（共 ７ 页） ∵ ｜ＱＡ ｜｜ＱＢ ｜ ＝ Ｓ△ＡＰＱ Ｓ△ＢＰＱ ∴ ｓｉｎ∠ＰＱＡ ＝ ｓｉｎ∠ＰＱＢ ∴ ∠ＰＱＡ ＝∠ＰＱＢ ∴ ｋＱＡ ＝ － ｋＱＢ ∴ ｙ１ －ｍ ｘ１ ＝ － ｙ２ －ｍ ｘ２ ∴ （ｍ － １）（ｘ１ ＋ ｘ２）＝ ２ｋｘ１ｘ２ １０ 分!!!!!!!!!!!!!!!!!! 即 －（ｍ － １） ４ｋ ２ｋ２ ＋ １ ＝ － ２ｋ ２ ２ｋ２ ＋ １ 解得 ｍ ＝ ２ ∴ 存在定点 Ｑ（０，２），使得 ｜ＱＡ ｜｜ＱＢ ｜ ＝ Ｓ△ＡＰＱ Ｓ△ＢＰＱ 恒成立 １２ 分!!!!!!!!!! ２２． （１２ 分） 解：（１）证明：ｆ ′（ｘ）＝ ｘ（ｅｘ － ｅ － ｘ）， 当 ｘ≥０ 时，ｅｘ≥１，ｅ － ｘ≤１， ∴ ｆ ′（ｘ）≥０， ∴ ｆ （ｘ）在［０，＋ ∞）上是增函数， 又 ｆ（０）＝ ０． ∴ ｆ（ｘ）≥０． ２ 分!!!!!!!!!!!!!!!!!!!!!!!!! 由 ｆ（ｘ）≤（ １ｘ ＋ １ ＋ ｘ － １）ｅ ｘ 整理得 （ｅｘ）２≥（ｘ ＋ １）２ 即　 ｅｘ≥ｘ ＋ １ ４ 分!!!!!!!!!!!!!!!!!!!!!!!! 令 φ（ｘ）＝ ｅｘ － ｘ － １（ｘ≥０），则 φ′（ｘ）＝ ｅｘ － １≥０， ∴ φ（ｘ）在［０，＋ ∞）上是增函数， 又 φ（ｘ）＝ ０ ∴ φ（ｘ）≥０ ∴ ｅｘ≥ｘ ＋ １ ∴ ｆ（ｘ）≤ １ ｘ ＋ １ ＋ ｘ( )－ １ ｅｘ 综上，０≤ｆ（ｘ）≤ １ ｘ ＋ １ ＋ ｘ( )－ １ ｅｘ ． ６ 分!!!!!!!!!!!!!!!! （２）当 ｘ∈［０，１］时，要证 ｆ（ｘ）≥ｇ（ｘ），即证 （ｘ ＋ １）ｅ － ｘ ＋（ｘ － １）ｅｘ≥ ａｘ ＋ ｘ ３ ２ ＋ ｘ ＋ ２ｘｃｏｓ( )ｘ ｅｘ， 只需证明（１ ＋ ｘ）ｅ － ２ｘ － ａｘ ＋ ｘ ３ ２ ＋ １ ＋ ２ｘｃｏｓ( )ｘ ≥０． ７ 分!!!!!!!!! 由（１）可知：当 ｘ∈［０，１］时，ｆ（ｘ）＝（ｘ ＋ １）ｅ － ｘ ＋（ｘ － １）ｅｘ≥０， 即（１ ＋ ｘ）ｅ － ２ｘ≥１ － ｘ， ∴ （１ ＋ ｘ）ｅ － ２ｘ － ａｘ ＋ ｘ ３ ２ ＋ １ ＋ ２ｘｃｏｓ( )ｘ ≥１ － ｘ － ａｘ － １ － ｘ３２ － ２ｘｃｏｓｘ ＝ － ｘ ａ ＋ １ ＋ ｘ ２ ２ ＋ ２ｃｏｓ( )ｘ ， 高三第二轮复习质量检测数学试题参考答案 第 ６ 页（共 ７ 页） 令 Ｇ（ｘ）＝ ｘ ２ ２ ＋ ２ｃｏｓｘ，则 Ｇ′（ｘ）＝ ｘ － ２ｓｉｎｘ． 令 Ｈ（ｘ）＝ ｘ － ２ｓｉｎｘ，则 Ｈ′（ｘ）＝ １ － ２ｃｏｓｘ， 当 ｘ∈［０，１］时，Ｈ′（ｘ）＜ ０， ∴ Ｇ′（ｘ）在［０，１］上是减函数， ∴ 当 ｘ∈［０，１］时，Ｇ′（ｘ）≤Ｇ′（０）＝ ０， ∴ Ｇ（ｘ）在［０，１］上是减函数， ∴ Ｇ（ｘ）≤Ｇ（０）＝ ２， ∴ ａ ＋ １ ＋ Ｇ（ｘ）≤ａ ＋ ３． ∴ 当 ａ≤ － ３ 时，ｆ（ｘ）≤ｇ（ｘ）在［０，１］上恒成立． ９ 分!!!!!!!!!! 当 ａ ＞ － ３ 时， 由（１）可知：ｅ２ｘ≥（ｘ ＋ １）２ 即（１ ＋ ｘ）ｅ － ２ｘ≤ １ ｘ ＋ １， ∴ （１ ＋ ｘ）ｅ － ２ｘ － ａｘ ＋ ｘ ３ ２ ＋ １ ＋ ２ｘｃｏｓ( )ｘ ≤ １ １ ＋ ｘ － １ － ａｘ － ｘ３ ２ － ２ｘｃｏｓｘ ＝ － ｘ１ ＋ ｘ － ａｘ － ｘ３ ２ － ２ｘｃｏｓｘ ＝ － ｘ １ ｘ ＋ １ ＋ ａ ＋ ｘ２ ２ ＋ ２ｃｏｓ( )ｘ ， １０ 分!!!!!!!!!!!!!!!!! 令 Ｉ（ｘ）＝ １ １ ＋ ｘ ＋ ａ ＋ ｘ２ ２ ＋ ２ｃｏｓｘ ＝ １ １ ＋ ｘ ＋ ａ ＋ Ｇ（ｘ），则 Ｉ′（ｘ）＝ － １ （１ ＋ ｘ）２ ＋ Ｇ′（ｘ）， 当 ｘ∈［０，１］时，Ｉ′（ｘ）＜ ０． ∴ Ｉ（ｘ）在［０，１］上是减函数， ∴ Ｉ（ｘ）在［０，１］上的值域为［ａ ＋ １ ＋ ２ｃｏｓ１，ａ ＋ ３］． ∵ ａ ＞ － ３ ∴ ａ ＋ ３ ＞ ０ ∴ 存在 ｘ０∈［０，１］，使得 Ｉ（ｘ０）＞ ０，此时 ｆ（ｘ０）＜ ｇ（ｘ０） ∴ 当 ａ ＞ － ３ 时，ｆ（ｘ）≥ｇ（ｘ）在［０，１］上不恒成立． 综上，实数 ａ的取值范围是（－ ∞，－ ３］． １２ 分!!!!!!!!!!!! 高三第二轮复习质量检测数学试题参考答案 第 ７ 页（共 ７ 页）