2020高中数学 第1章 点、直线、面的位置关系2 空间中两条直线的位置关系学案 苏教版必修2

2020高中数学 第1章 点、直线、面的位置关系2 空间中两条直线的位置关系学案 苏教版必修2

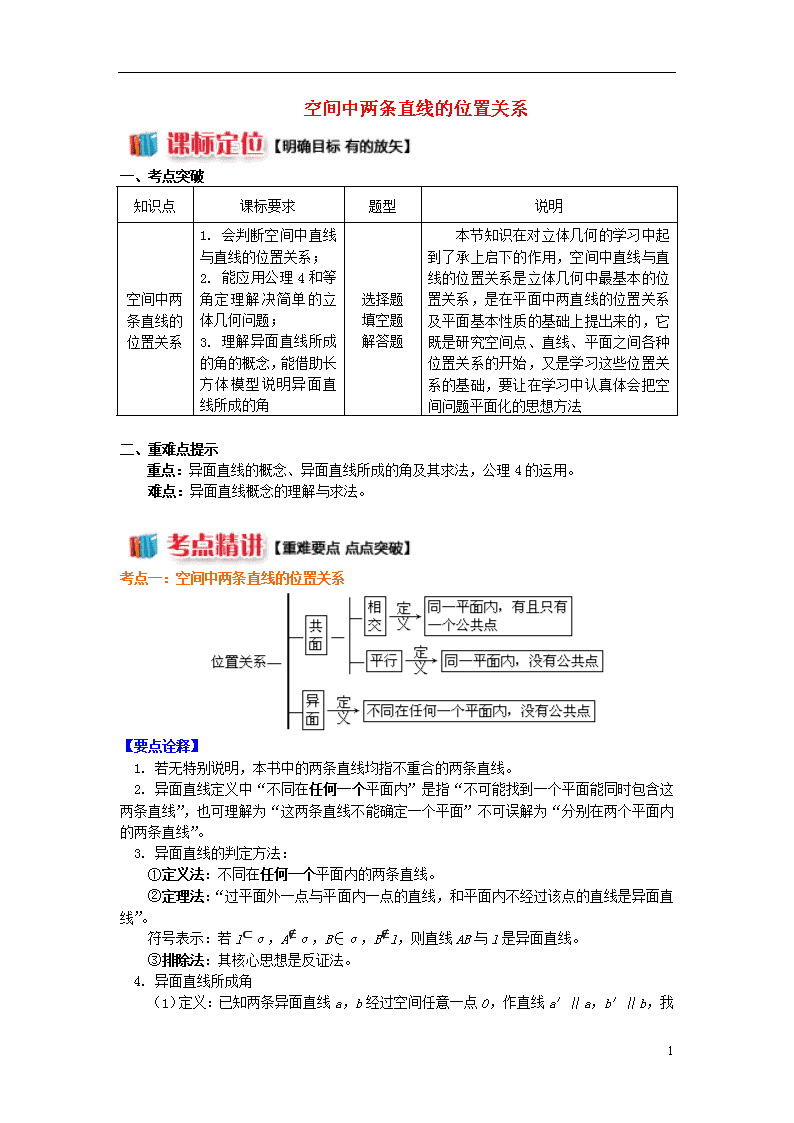
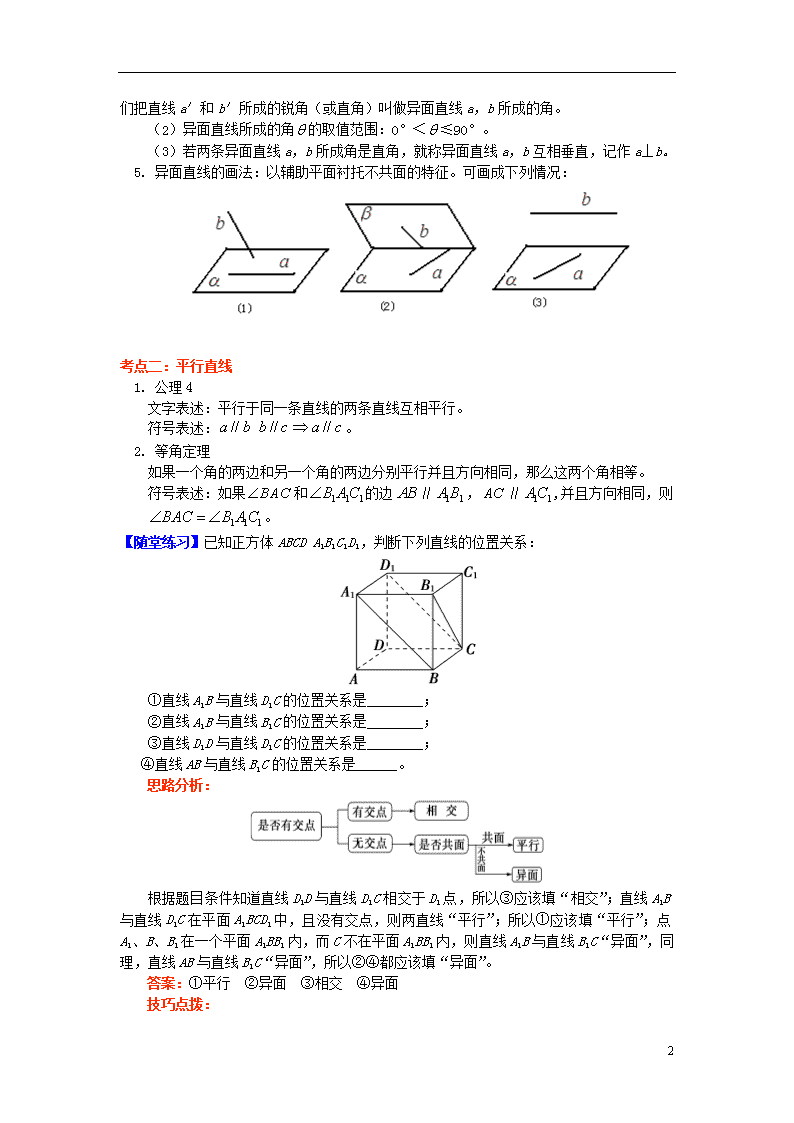
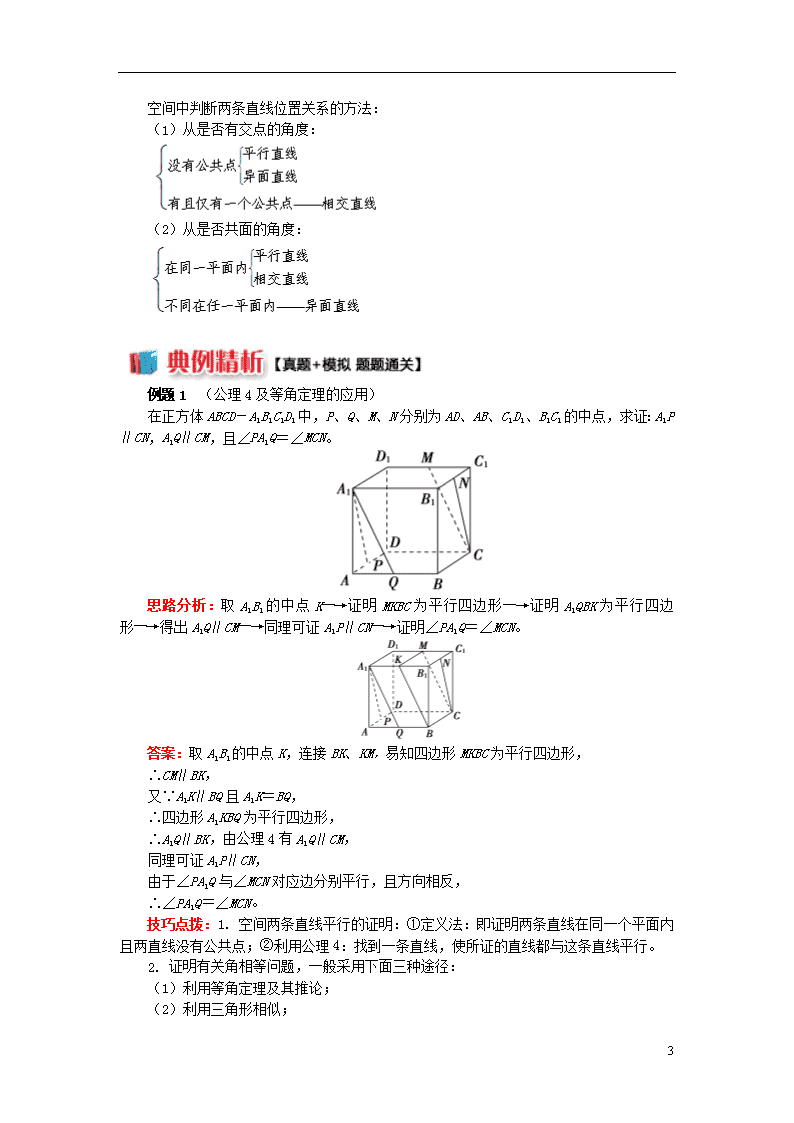
空间中两条直线的位置关系 一、考点突破 知识点 课标要求 题型 说明 空间中两条直线的位置关系 ‎1. 会判断空间中直线与直线的位置关系；‎ ‎2. 能应用公理4和等角定理解决简单的立体几何问题；‎ ‎3. 理解异面直线所成的角的概念，能借助长方体模型说明异面直线所成的角 ‎ 选择题 填空题 解答题 本节知识在对立体几何的学习中起到了承上启下的作用，空间中直线与直线的位置关系是立体几何中最基本的位置关系，是在平面中两直线的位置关系及平面基本性质的基础上提出来的，它既是研究空间点、直线、平面之间各种位置关系的开始，又是学习这些位置关系的基础，要让在学习中认真体会把空间问题平面化的思想方法 二、重难点提示 重点：异面直线的概念、异面直线所成的角及其求法，公理4的运用。‎ 难点：异面直线概念的理解与求法。‎ 考点一：空间中两条直线的位置关系 ‎【要点诠释】‎ ‎1. 若无特别说明，本书中的两条直线均指不重合的两条直线。‎ ‎2. 异面直线定义中“不同在任何一个平面内”是指“不可能找到一个平面能同时包含这两条直线”，也可理解为“这两条直线不能确定一个平面”不可误解为“分别在两个平面内的两条直线”。‎ ‎3. 异面直线的判定方法：‎ ‎①定义法：不同在任何一个平面内的两条直线。‎ ‎②定理法：“过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线”。‎ 符号表示：若l⊂α，A∉α，B∈α，B∉l，则直线AB与l是异面直线。‎ ‎③排除法：其核心思想是反证法。‎ ‎4. 异面直线所成角 ‎（1）定义：已知两条异面直线a，b经过空间任意一点O，作直线a′∥a，b′∥b 6‎ ‎，我们把直线a′和b′所成的锐角（或直角）叫做异面直线a，b所成的角。‎ ‎（2）异面直线所成的角的取值范围：0°＜≤90°。‎ ‎（3）若两条异面直线a，b所成角是直角，就称异面直线a，b互相垂直，记作a⊥b。‎ ‎5. 异面直线的画法：以辅助平面衬托不共面的特征。可画成下列情况：‎ 考点二：平行直线 ‎1. 公理4‎ 文字表述：平行于同一条直线的两条直线互相平行。‎ 符号表述：。‎ ‎2. 等角定理 如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。‎ 符号表述：如果和的边∥，∥,并且方向相同，则 ‎。‎ ‎【随堂练习】已知正方体ABCDA1B‎1C1D1，判断下列直线的位置关系：‎ ‎①直线A1B与直线D‎1C的位置关系是________；‎ ‎②直线A1B与直线B‎1C的位置关系是________；‎ ‎③直线D1D与直线D‎1C的位置关系是________；‎ ‎④直线AB与直线B‎1C的位置关系是______。‎ 思路分析：‎ 根据题目条件知道直线D1D与直线D‎1C相交于D1点，所以③应该填“相交”；直线A1B与直线D‎1C在平面A1BCD1中，且没有交点，则两直线“平行”；所以①应该填“平行”；点A1、B、B1在一个平面A1BB1内，而C不在平面A1BB1内，则直线A1B与直线B‎1C“异面”，同理，直线AB与直线B‎1C“异面”，所以②④都应该填“异面”。‎ 答案：①平行　②异面　③相交　④异面 技巧点拨：‎ 6‎ 空间中判断两条直线位置关系的方法：‎ ‎（1）从是否有交点的角度：‎ ‎（2）从是否共面的角度：‎ 例题1 （公理4及等角定理的应用）‎ 在正方体ABCD－A1B‎1C1D1中，P、Q、M、N分别为AD、AB、C1D1、B‎1C1的中点，求证：A1P∥CN，A1Q∥CM，且∠PA1Q＝∠MCN。‎ 思路分析：取A1B1的中点K―→证明MKBC为平行四边形―→证明A1QBK为平行四边形―→得出A1Q∥CM―→同理可证A1P∥CN―→证明∠PA1Q＝∠MCN。‎ 答案：取A1B1的中点K，连接BK、KM，易知四边形MKBC为平行四边形，‎ ‎∴CM∥BK，‎ 又∵A1K∥BQ且A1K＝BQ，‎ ‎∴四边形A1KBQ为平行四边形，‎ ‎∴A1Q∥BK，由公理4有A1Q∥CM，‎ 同理可证A1P∥CN，‎ 由于∠PA1Q与∠MCN对应边分别平行，且方向相反，‎ ‎∴∠PA1Q＝∠MCN。‎ 技巧点拨：1. 空间两条直线平行的证明：①定义法：即证明两条直线在同一个平面内且两直线没有公共点；②利用公理4：找到一条直线，使所证的直线都与这条直线平行。‎ ‎2. 证明有关角相等问题，一般采用下面三种途径：‎ ‎（1）利用等角定理及其推论；‎ ‎（2）利用三角形相似；‎ 6‎ ‎（3）利用三角形全等。‎ 本例题是通过第一种途径来实现解答的，请同学们考虑利用第三种途径予以证明。‎ 例题2 （异面直线所成的角）‎ 如图，在正方体ABCD－A1B‎1C1D1中，求下列异面直线所成的角。‎ ‎（1）AA1与BC；‎ ‎（2）DD1与A1B；‎ ‎（3）A1B与AC。‎ 思路分析：‎ 答案：（1）∵ABCD－A1B‎1C1D1为正方体，‎ ‎∴AA1∥BB1，‎ 又BB1⊥BC，‎ ‎∴AA1⊥BC，‎ ‎∴AA1与BC所成的角为90°；‎ ‎（2）又DD1∥A‎1A，在正方形A1ABB1中，∠BA‎1A＝45°，‎ 故DD1与A1B所成的角为45°；‎ ‎（3）∵A‎1AC‎1C，∴四边形A1ACC1为平行四边形，‎ ‎∴A‎1C1∥AC，‎ 在△A1BC1中，A1B＝BC1＝A‎1C1，‎ ‎∴∠BA‎1C1＝60°.‎ 故A1B与AC所成的角为60°。‎ 技巧点拨：1. 求两条异面直线所成角的关键是作出异面直线所成的角，作两条异面直线所成角的方法是：将其中一条平移到某个位置使其与另一条相交或是将两条异面直线同时平移到某个位置使它们相交。‎ ‎2. 对于平移点的选取，为了方便计算，该点常选在两条异面直线中的一条直线上，如端点、中点等。‎ 异面直线所成角的求法 6‎ ‎【满分训练】正方体AC1中，E、F分别是A1B1、B‎1C1的中点，求异面直线DB1与EF所成角的大小。‎ 思路分析：本题主要考查异面直线所成角的求法，关键是作出异面直线所成的角，根据定义作出角，即可求解。‎ 答案：方法一　如图，连接A‎1C1，B1D1，并设它们相交于点O，取DD1的中点G，连接OG，‎ 则OG∥B1D，EF∥A‎1C1，‎ ‎∴∠GOA1为异面直线DB1与EF所成的角或其补角，‎ ‎∵GA1＝GC1，O为A‎1C1的中点，∴GO⊥A‎1C1，‎ ‎∴异面直线DB1与EF所成的角为90°。‎ 方法二　如图，连接A1D，取A1D的中点H，连接HE，则HE∥DB1，‎ ‎∴∠HEF为所求异面直线DB1与EF所成的角或其补角，‎ 连接HF，设AA1＝1，则EF＝，HE＝，‎ 取A1D1的中点I，连接IF，IH，则HI⊥IF，‎ ‎∴HF2＝HI2＋IF2＝，∴HF2＝EF2＋HE2，‎ ‎∴∠HEF＝90°，∴异面直线DB1与EF所成的角为90°。‎ 方法三　分别取AA1，CC1的中点M，N，连接MN，则MN∥EF，如图所示，‎ 连接DM，B1N，则B1N∥DM，‎ ‎∴四边形DMB1N为平行四边形，‎ 6‎ ‎∴MN与DB1必相交，设交点为P，‎ ‎∴∠DPM为异面直线DB1与EF所成的角或其补角，‎ 设AA1＝1，则MP＝，DM＝，DP＝，‎ ‎∴DM2＝DP2＋MP2，∴∠DPM＝90°，∴DB1⊥EF，‎ ‎∴异面直线DB1与EF所成的角为90°。‎ 方法四　在原正方体的右侧补上一个与其全等的正方体，连接B1Q，则B1Q∥EF，如图，‎ ‎∴直线DB1与B1Q所成的较小的角就是异面直线DB1与EF所成的角，‎ 通过计算，不难得到：B1D2＋B1Q2＝DQ2，‎ ‎∴异面直线DB1与EF所成的角为90°。‎ 技巧点拨：1. 求两条异面直线所成角的步骤：‎ ‎（1）恰当选点，用平移法构造出一个相交角；‎ ‎（2）证明这个角就是异面直线所成的角（或其补角），‎ ‎（3）把相交角放在平面图形中，一般是放在三角形中，通过解三角形求出所构造的角的度数；‎ ‎（4）给出结论：若求出的平面角是锐角或直角，则它就是两条异面直线所成的角；若求出的角是钝角，则它的补角才是两条异面直线所成的角。‎ ‎2. 构造异面直线所成角的方法有：①平移法；②补形法（如解法四）。‎ 6‎