高中数学人教a版选修4-1学业分层测评4相似三角形的性质word版含解析

高中数学人教a版选修4-1学业分层测评4相似三角形的性质word版含解析

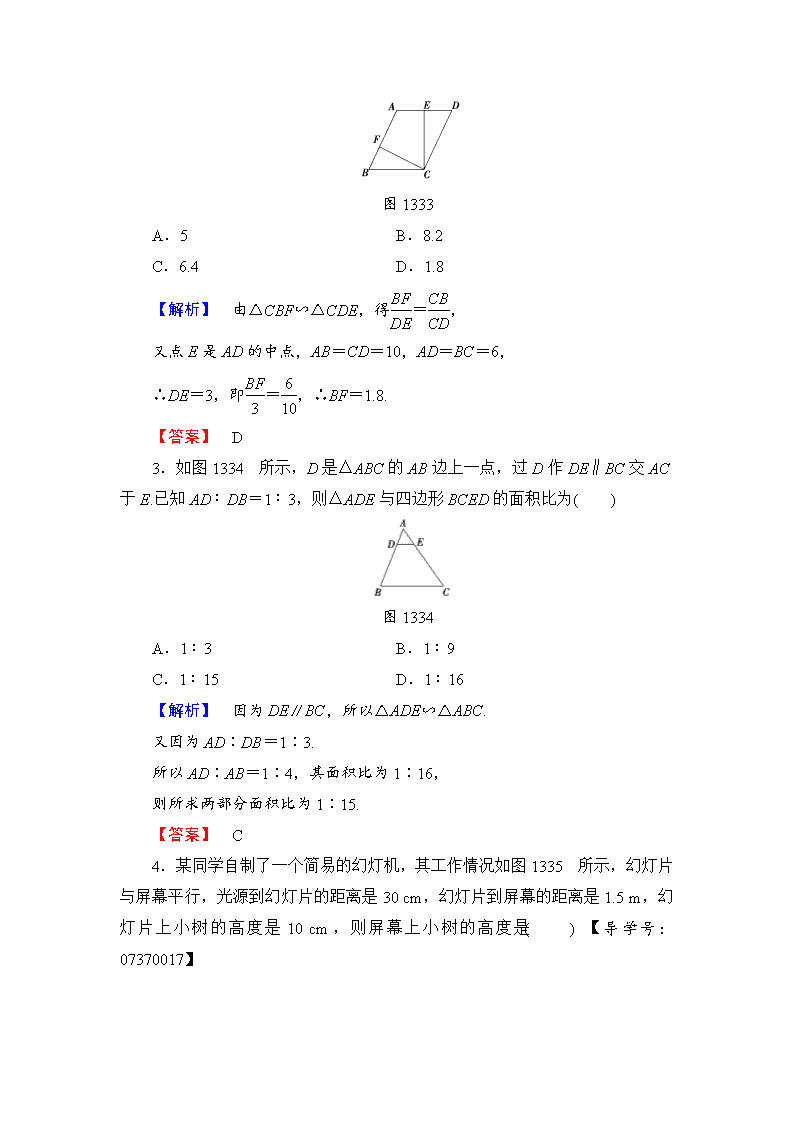
学业分层测评(四) (建议用时：45 分钟) [学业达标] 一、选择题 1．如图 1332，D，E，F 是△ABC 的三边中点，设△DEF 的面积为1 4 ，△ ABC 的周长为 9，则△DEF 的周长与△ABC 的面积分别是( ) 图 1332 A.9 2 ，1 B．9,4 C.9 2 ，8 D.9 4 ，16 【解析】 ∵D，E，F 分别为△ABC 三边的中点， ∴EF 綊 1 2BC，DE 綊 1 2AC，DF 綊 1 2AB. ∴△DFE∽△ABC，且EF BC ＝1 2 ，∴l△DEF l△ABC ＝EF BC ＝1 2. 又∵l△ABC＝9，∴l△DEF＝9 2. 又∵S△DEF S△ABC ＝EF2 BC2 ＝1 4 ，S△DEF＝1 4 ， ∴S△ABC＝1，故选 A. 【答案】 A 2．如图 1333，在▱ABCD 中，AB＝10，AD＝6，E 是 AD 的中点，在 AB 上取一点 F，使△CBF∽△CDE，则 BF 的长是( ) 图 1333 A．5 B．8.2 C．6.4 D．1.8 【解析】 由△CBF∽△CDE，得BF DE ＝CB CD ， 又点 E 是 AD 的中点，AB＝CD＝10，AD＝BC＝6， ∴DE＝3，即BF 3 ＝ 6 10 ，∴BF＝1.8. 【答案】 D 3．如图 1334 所示，D 是△ABC 的 AB 边上一点，过 D 作 DE∥BC 交 AC 于 E.已知 AD∶DB＝1∶3，则△ADE 与四边形 BCED 的面积比为( ) 图 1334 A．1∶3 B．1∶9 C．1∶15 D．1∶16 【解析】 因为 DE∥BC，所以△ADE∽△ABC. 又因为 AD∶DB＝1∶3. 所以 AD∶AB＝1∶4，其面积比为 1∶16， 则所求两部分面积比为 1∶15. 【答案】 C 4．某同学自制了一个简易的幻灯机，其工作情况如图 1335 所示，幻灯片 与屏幕平行，光源到幻灯片的距离是 30 cm，幻灯片到屏幕的距离是 1.5 m，幻 灯片上小树的高度是 10 cm，则屏幕上小树的高度是( ) 【导学号：07370017】 图 1335 A．50 cm B．500 cm C．60 cm D．600 cm 【解析】 设屏幕上小树的高度为 x cm，则10 x ＝ 30 30＋150 ，解得 x＝60(cm)． 【答案】 C 5．如图 1336，△ABC 中，DE∥BC，DE 分别交 AB，AC 于 D，E，S△ADE ＝2S△DCE，则S△ADE S△ABC ＝( ) 图 1336 A.1 4 B.1 2 C.2 3 D.4 9 【解析】 ∵DE∥BC，∴△ADE∽△ABC， 由 S△ADE＝2S△DCE，得AD AB ＝2 3 ，∴S△ADE S△ABC ＝4 9. 【答案】 D 二、填空题 6．如图 1337，在△ABC 中，D 为 AC 边上的中点，AE∥BC，ED 交 AB 于 G，交 BC 延长线于 F，若 BG∶GA＝3∶1，BC＝10，则 AE 的长为________． 图 1337 【解析】 ∵AE∥BC，∴△BGF∽△AGE，∴BF AE ＝BG GA ＝3 1 ， ∵D 为 AC 中点，∴AE CF ＝AD DC ＝1，∴AE＝CF， ∴BC∶AE＝2∶1，∵BC＝10，∴AE＝5. 【答案】 5 7．如图 1338，AB 与 CD 相交于点 E，过 E 作 BC 的平行线与 AD 的延长 线交于点 P，已知∠A＝∠C，PD＝2DA＝2，则 PE＝________. 图 1338 【解析】 因为 PE∥BC，所以∠C＝∠PED.又因为∠C＝∠A，所以∠A＝ ∠PED.又∠P＝∠P，所以△PDE∽△PEA，则PD PE ＝PE PA ，即 PE2＝PD·PA＝2×3 ＝6，故 PE＝ 6. 【答案】 6 8．(2016·湛江高三调研)如图 1339，在△ABC 中，已知 DE∥BC，△ADE 的面积是 a2，梯形 DBCE 的面积是 8a2，则AD AB ＝________. 图 1339 【解析】 ∵S△ADE＝a2，SDBCE＝8a2，∴S△ABC＝S△ADE＋SBDCE＝a2＋8a2＝9a2， ∴ AD AB 2＝S△ADE S△ABC ＝ a2 9a2 ＝1 9 ，∴AD AB ＝1 3. 【答案】 1 3 三、解答题 9．如图 1340，已知在△ABC 中，D 是 BC 边的中点，且 AD＝AC，DE⊥ BC，DE 与 AB 相交于点 E，EC 与 AD 相交于点 F. 图 1340 (1)求证：△ABC∽△FCD； (2)若 S△FCD＝5，BC＝10，求 DE 的长． 【解】 (1)证明：∵DE⊥BC，D 是 BC 的中点， ∴EB＝EC，∴∠B＝∠1， 又∵AD＝AC， ∴∠2＝∠ACB. ∴△ABC∽△FCD. (2)过点 A 作 AM⊥BC，垂足为点 M. ∵△ABC∽△FCD，BC＝2CD， ∴S△ABC S△FCD ＝ BC CD 2＝4. 又∵S△FCD＝5，∴S△ABC＝20. ∵S△ABC＝1 2BC·AM，BC＝10， ∴20＝1 2 ×10×AM，∴AM＝4. 又∵DE∥AM，∴DE AM ＝BD BM. ∵DM＝1 2DC＝1 4BC＝5 2 ， BM＝BD＋DM， BD＝1 2BC＝5，∴DE 4 ＝ 5 5＋5 2 ， ∴DE＝8 3. 10．如图 1341，△ABC 是一块锐角三角形余料，边 BC＝200 mm，高 AD ＝300 mm，要把它加工成长是宽的 2 倍的矩形零件，使矩形较短的边在 BC 上， 其余两个顶点分别在 AB，AC 上，求这个矩形零件的边长． 图 1341 【解】 设矩形 EFGH 为加工成的矩形零件，边 FG 在 BC 上，则点 E，H 分别在 AB，AC 上，△ABC 的高 AD 与边 EH 相交于点 P，设矩形的边 EH 的长 为 x mm. ∵EH∥BC，∴△AEH∽△ABC， ∴AP AD ＝EH BC ，∴300－2x 300 ＝ x 200 ， 解得 x＝600 7 (mm)，2x＝1 200 7 (mm)． 答：加工成的矩形零件的边长分别为 600 7 mm 和 1 200 7 mm. [能力提升] 1．如图 1342 所示，已知在△ABC 中，∠C＝90°，正方形 DEFG 内接于△ ABC，DE∥AC，EF∥BC，AC＝1，BC＝2，则 AF∶FC 等于( ) 图 1342 A．1∶3 B．1∶4 C．1∶2 D．2∶3 【解析】 设正方形边长为 x，则由△AFE∽△ACB， 可得 AF∶AC＝FE∶CB，即x 2 ＝1－x 1 ， 所以 x＝2 3 ，于是AF FC ＝1 2. 【答案】 C 2．如图 1343，AB∥EF∥CD，已知 AB＝20，DC＝80，那么 EF 的值是 ( ) 图 1343 A．10 B．12 C．16 D．18 【解析】 ∵AB∥EF∥CD， ∴AE EC ＝AB DC ＝20 80 ＝1 4 ， ∴EF AB ＝EC AC ＝4 5 ， ∴EF＝4 5AB＝4 5 ×20＝16. 【答案】 C 3．在△ABC 中，如图 1344 所示，BC＝m，DE∥BC，DE 分别交 AB，AC 于 E，D 两点，且 S△ADE＝S 四边形 BCDE，则 DE＝________. 【导学号：07370018】 图 1344 【解析】 ∵DE∥BC， ∴△ADE∽△ACB. 又∵S△ADE＋S 四边形 BCDE＝S△ABC；S△ADE＝S 四边形 BCDE， ∴S△ADE＝1 2S△ABC， ∴ DE BC 2＝1 2 ，∴ DE m 2＝1 2 ， ∴DE＝ 2 2 m. 【答案】 2 2 m 4．某生活小区的居民筹集资金1 600元，计划在一块上、下两底分别为10 cm、 20 cm 的梯形空地上种植花木． (1)他们在△AMD 和△BMC 地带上种植太阳花，单价为 8 元/m2，当△AMD 地带种满花后(如图 1345 阴影部分)共花了 160 元，请计算种满△BMC 地带所 需的费用； 图 1345 (2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为 12 元 /m2 和 10 元/m2，应选择种哪种花木可以刚好用完所筹集的资金？ 【解】 (1)∵四边形 ABCD 是梯形，∴AD∥BC， ∴△AMD∽△CMB，∴S△AMD S△CMB ＝ AD BC 2＝1 4. ∵种植△AMD 地带花费 160 元， ∴S△AMD＝160 8 ＝20 (m2)，∴S△CMB＝80 (m2)． ∴△BMC 地带的花费为 80×8＝640(元)． (2)设△AMD，△BMC 的高分别为 h1，h2，梯形 ABCD 的高为 h， ∵S△AMD＝1 2 ×10h1＝20，∴h1＝4(m)． 又∵h1 h2 ＝1 2 ，∴h2＝8(m)． ∴h＝h1＋h2＝12(m)． ∴S 梯形 ABCD＝1 2(AD＋BC)h＝1 2 ×30×12 ＝180 (m2)， ∴S△AMB＋S△DMC＝180－20－80＝80 (m2)． ∴160＋640＋80×12＝1 760(元)， 160＋640＋80×10＝1 600(元)． ∴应种植茉莉花刚好用完所筹资金．