2021高三数学人教B版一轮学案：第八章 第五节　第1课时　椭圆及其几何性质

2021高三数学人教B版一轮学案：第八章 第五节　第1课时　椭圆及其几何性质

www.ks5u.com 第五节　椭圆 最新考纲 考情分析 ‎1.掌握椭圆的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率)．‎ ‎2．了解椭圆的简单应用．‎ ‎3．理解数形结合的思想.‎ ‎1.椭圆的定义、标准方程、几何性质以及椭圆与其他知识综合应用是近几年高考命题的热点．‎ ‎2．常与直线、向量、三角等知识交汇考查，考查学生分析问题、解决问题的能力．‎ ‎3．三种题型都有可能出现，选择、填空题一般为中低档题，解答题为高档题.‎ ‎　　　　　　　　　　　　　　　　‎ 知识点一　　椭圆的定义 平面内到两定点F1，F2的距离的和等于常数(大于|F‎1F2|)的点的轨迹叫做椭圆．两定点F1，F2叫做椭圆的焦点．‎ 集合P＝{M||MF1|＋|MF2|＝‎2a}，|F‎1F2|＝‎2c，其中a>0，c>0，且a，c为常数．‎ ‎ (1)当‎2a>|F‎1F2|时，M点的轨迹是椭圆；‎ ‎(2)当‎2a＝|F‎1F2|时，M点的轨迹是线段F‎1F2；‎ ‎(3)当‎2a<|F‎1F2|时，M点不存在．‎ 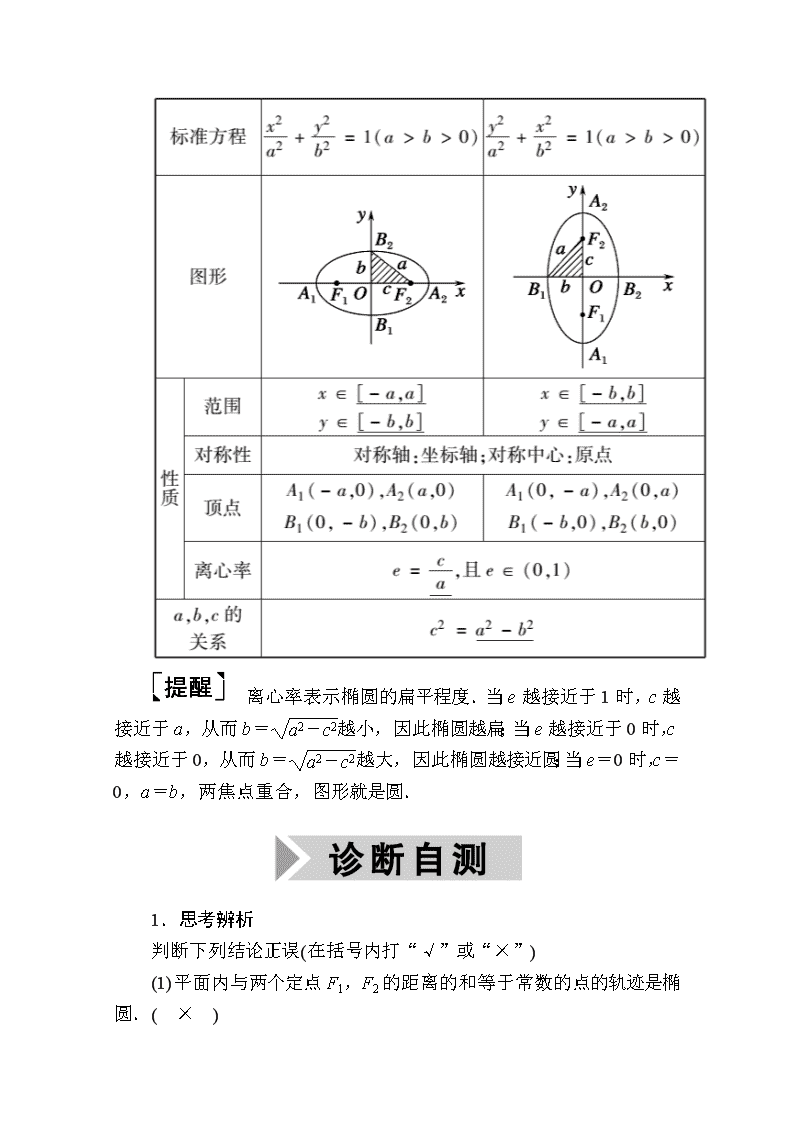知识点二　　　椭圆的标准方程和几何性质 离心率表示椭圆的扁平程度．当e越接近于1时，c越接近于a，从而b＝越小，因此椭圆越扁；当e越接近于0时，c越接近于0，从而b＝越大，因此椭圆越接近圆；当e＝0时，c＝0，a＝b，两焦点重合，图形就是圆．‎ ‎1．思考辨析 判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)平面内与两个定点F1，F2的距离的和等于常数的点的轨迹是椭圆．(　×　)‎ ‎(2)椭圆是轴对称图形，也是中心对称图形．(　√　)‎ ‎(3)椭圆的离心率e越大，椭圆就越圆．(　×　)‎ ‎(4)方程mx2＋ny2＝1(m>0，n>0，m≠n)表示的曲线是椭圆．(　√　)‎ ‎(5)＋＝1(a≠b)表示焦点在y轴上的椭圆．(　×　)‎ ‎(6)＋＝1(a>b>0)与＋＝1(a>b>0)的焦距相等．(　√　)‎ ‎2．小题热身 ‎(1)已知椭圆的方程为2x2＋3y2＝m(m>0)，则此椭圆的离心率为(　B　)‎ A. B. C. D. 解析：由题意得椭圆的标准方程为＋＝1，所以a2＝，b2＝，所以c2＝a2－b2＝，e2＝＝，e＝.‎ ‎(2)已知中心在原点的椭圆C的右焦点为F(1,0)，离心率等于，则椭圆C的方程是(　D　)‎ A.＋＝1 B.＋＝1‎ C.＋＝1 D.＋＝1‎ 解析：设椭圆的标准方程为＋＝1(a>b>0)．‎ 因为椭圆的一个焦点为F(1,0)，离心率e＝，‎ 所以解得 故椭圆C的标准方程为＋＝1.‎ ‎(3)已知椭圆C：＋＝1的一个焦点为(2,0)，则C的离心率为(　C　)‎ A. B. C. D. 解析：∵a2＝4＋22＝8，∴a＝2，‎ ‎∴e＝＝＝.‎ ‎(4)若方程＋＝1表示椭圆，则k的取值范围是(3,4)∪(4,5)．‎ 解析：由已知得解得3b>0)的左、右焦点，B为C的短轴的一个端点，直线BF1与C的另一个交点为A，若△BAF2为等腰三角形，则＝(　　)‎ A. B. C. D．3‎ ‎(2)(2020·郑州市质量预测)椭圆＋＝1的焦点为F1，F2，P为椭圆上一点，若∠F1PF2＝60°，则△F1PF2的面积是(　　)‎ A. B. C．16 D．32 ‎【解析】　(1)如图，不妨设点B在y轴的正半轴上，根据椭圆的定义，得|BF1|＋|BF2|＝‎2a，|AF1|＋|AF2|＝‎2a，由题意知|AB|＝|AF2|，所以|BF1|＝|BF2|＝a，|AF1|＝，|AF2|＝.所以＝.故选A.‎ ‎(2)由椭圆＋＝1的焦点为F1，F2知，|F‎1F2|＝‎2c＝6，在△F1PF2中，不妨设|PF1|＝m，|PF2|＝n，则|PF1|＋|PF2|＝m＋n＝‎2a＝10，在△F1‎ PF2中，由余弦定理|F‎1F2|2＝|PF1|2＋|PF2|2－2|PF1|·|PF2|cos∠F1PF2，得(‎2c)2＝m2＋n2－‎2m·ncos60°，即‎4c2＝(m＋n)2－3mn＝‎4a2－3mn，解得mn＝，所以S△F1PF2＝·|PF1|·|PF2|sin∠F1PF2＝mnsin60°＝.故选A.‎ ‎【答案】　(1)A　(2)A 方法技巧 (1)椭圆定义的应用主要有两个方面：一是利用定义求椭圆的标准方程；二是利用定义求焦点三角形的周长和面积、弦长、最值、离心率等.通常定义和余弦定理结合使用，求解关于焦点三角形的周长和面积问题.‎ (2)椭圆的定义式|PF1|＋|PF2|＝‎2a中必须强调‎2a>|F‎1F2|.‎ ‎1．已知F1，F2是椭圆C：＋＝1(a>b>0)的两个焦点，P为椭圆C上的一点，且⊥.若△PF‎1F2的面积为9，则b＝3.‎ 解析：设|PF1|＝r1，|PF2|＝r2，则 ‎∴2r1r2＝(r1＋r2)2－(r＋r)＝‎4a2－‎4c2＝4b2，‎ ‎∴S△PF‎1F2＝r1r2＝b2＝9，∴b＝3.‎ ‎2．已知F是椭圆5x2＋9y2＝45的左焦点，P是此椭圆上的动点，A(1,1)是一定点，则|PA|＋|PF|的最大值为6＋，最小值为6－.‎ 解析：椭圆方程化为＋＝1，‎ 设F1是椭圆的右焦点，则F1(2,0)，‎ ‎∴|AF1|＝，∴|PA|＋|PF|＝|PA|－|PF1|＋6，‎ 又－|AF1|≤|PA|－|PF1|≤|AF1|(当P，A，F1共线时等号成立)，∴6－≤|PA|＋|PF|≤6＋.‎ 考点二　椭圆的标准方程 命题方向1　　定义法 ‎【例2】　(2019·全国卷Ⅰ)已知椭圆C的焦点为F1(－1，0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为(　　)‎ A.＋y2＝1 B.＋＝1‎ C.＋＝1 D.＋＝1‎ ‎【解析】　方法1：由题意设椭圆的方程为＋＝1(a>b>0)，连接F‎1A，令|F2B|＝m，则|AF2|＝‎2m，|BF1|＝‎3m.由椭圆的定义知，‎4m＝‎2a，得m＝，故|F‎2A|＝a＝|F‎1A|，则点A为椭圆C的上顶点或下顶点．令∠OAF2＝θ(O为坐标原点)，则sinθ＝.在等腰三角形ABF1中，cos2θ＝＝，所以＝1－2()2，得a2＝3.又c2＝1，所以b2＝a2－c2＝2，椭圆C的方程为＋＝1.故选B.‎ 方法2：设|F2B|＝x(x>0)，则|AF2|＝2x，|AB|＝3x，|BF1|＝3x，|AF1|＝‎4a－(|AB|＋|BF1|)＝‎4a－6x，由椭圆的定义知|BF1|＋|BF2|＝‎2a＝4x，所以|AF1|＝2x.‎ 在△BF‎1F2中，由余弦定理得|BF1|2＝|BF2|2＋|F‎1F2|2‎ ‎－2|F2B|·|F‎1F2|cos∠BF‎2F1，即 ‎9x2＝x2＋22－4x·cos∠BF‎2F1①，‎ 在△AF‎1F2中，由余弦定理可得|AF1|2＝|AF2|2＋|F‎1F2|2－2|AF2|·|F‎1F2|cos∠AF‎2F1，即 ‎4x2＝4x2＋22＋8x·cos∠BF‎2F1②，‎ 由①②得x＝，所以‎2a＝4x＝2，a＝，‎ 所以b2＝a2－c2＝2.‎ 所以椭圆的方程为＋＝1.故选B.‎ ‎【答案】　B 命题方向2　　待定系数法 ‎【例3】　(1)已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点，(，)，则椭圆方程为________．‎ ‎(2)一个椭圆的中心在原点，坐标轴为对称轴，焦点F1，F2在x轴上，P(2，)是椭圆上一点，且|PF1|，|F‎1F2|，|PF2|成等差数列，则椭圆方程为________．‎ ‎【解析】　(1)设椭圆方程为mx2＋ny2＝1(m，n>0，m≠n)．‎ 由解得m＝，n＝.‎ ‎∴椭圆方程为＋＝1.‎ ‎(2)∵椭圆的中心在原点，焦点F1，F2在x轴上，∴可设椭圆方程为＋＝1(a>b>0)，∵P(2，)是椭圆上一点，且|PF1|，|F‎1F2|，|PF2|成等差数列，‎ ‎∴又a2＝b2＋c2，‎ ‎∴a＝2，b＝，c＝，‎ ‎∴椭圆方程为＋＝1.‎ ‎【答案】　(1)＋＝1　(2)＋＝1‎ 方法技巧 ‎(1)求椭圆的标准方程多采用定义法和待定系数法．‎ ‎(2)利用定义法求椭圆方程，要注意条件‎2a>|F‎1F2|；利用待定系数法要先定形(焦点位置)，再定量，也可把椭圆方程设为mx2＋ny2＝1(m>0，n>0，m≠n)的形式．‎ ‎1．(方向1)已知椭圆C：＋＝1(a>b>0)的左、右焦点为F1，F2，离心率为，过F2的直线l交C于A，B两点．若△AF1B的周长为4，则C的方程为(　A　)‎ A.＋＝1 B.＋y2＝1‎ C.＋＝1 D.＋＝1‎ 解析：由已知及椭圆的定义知‎4a＝4，即a＝，‎ 又＝＝，所以c＝1，b2＝2，‎ 所以C的方程为＋＝1.‎ ‎2．(方向2)设F1，F2分别是椭圆E：x2＋＝1(0b>0)，如图所示，∵△PF‎1F2为直角三角形，∴PF1⊥F‎1F2，又|PF1|＝|F‎1F2|＝‎2c，∴|PF2|＝‎2c，∴|PF1|＋|PF2|＝‎2c＋‎2c＝‎2a，∴椭圆E的离心率e＝＝－1.故选A.‎ ‎【答案】　A 命题方向3　　最值或范围问题 ‎【例6】　已知椭圆＋＝1(a>b>0)的长轴长是短轴长的倍，且过点(2，)．‎ ‎(1)求椭圆的标准方程．‎ ‎(2)若△OAB的顶点A，B在椭圆上，OA所在的直线斜率为k1，OB所在的直线斜率为k2，若k1·k2＝－，求·的最大值．‎ ‎【解】　(1)由已知，解得 所以椭圆的标准方程为＋＝1.‎ ‎(2)设A(x1，y1)，B(x2，y2)，不妨设x1>0，x2>0.‎ 由k1k2＝－＝－得k2＝－(k1≠0)，‎ 直线OA，OB的方程分别为y＝k1x，y＝k2x，‎ 联立解得x1＝，‎ 同理，x2＝，‎ 所以x2＝＝.‎ 因为·＝x1x2＋y1y2＝x1x2‎ ‎＝＝≤＝2，‎ 当且仅当|k1|＝时，等号成立．‎ 所以·的最大值为2.‎ 方法技巧 ‎1.求椭圆离心率的方法 (1)直接求出a，c的值，利用离心率公式直接求解.‎ (2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝a2－c2消去b，转化为含有e的方程(或不等式)求解.‎ ‎2.在求与椭圆有关的一些量的范围，或者最值时，经常用到椭圆标准方程中x，y的范围、离心率的范围等不等关系.‎ ‎1．(方向1)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1，则椭圆长轴长的最小值为(　D　)‎ A．1 B. C．2 D．2 解析：设a，b，c分别为椭圆的长半轴长、短半轴长、半焦距，依题意知，当三角形的高为b时面积最大，所以×2cb＝1，bc＝1，而‎2a＝2≥2＝2(当且仅当b＝c＝1时取等号)，即长轴长‎2a的最小值为2.‎ ‎2．(方向2)(2020·河北省衡水市高三大联考)已知椭圆O：＋＝1(a>)的左、右焦点分别为F1，F2，过左焦点F1的直线l与椭圆的一个交点为M，右焦点F2关于直线l的对称点为P，若△F1MP为正三角形，且其面积为，则该椭圆的离心率为(　C　)‎ A. B. C. D. 解析：设正△F1MP的边长为m，则m2＝，∴m＝2.‎ 又由椭圆的定义可知|MF1|＋|MF2|＝|MF1|＋|MP|＝4，∴‎2a＝4，解得a＝2，又由题可知b＝，∴c＝1，e＝＝.故选C.‎ ‎3．(方向2)(2020·豫南九校联考)已知两定点A(－1,0)和B(1,0)，动点P(x，y)在直线l：y＝x＋3上移动，椭圆C以A，B为焦点且经过点P，则椭圆C的离心率的最大值为(　A　)‎ A. B. C. D. 解析：不妨设椭圆方程为＋＝1(a>1)，与直线l的方程联立 消去y得(‎2a2－1)x2＋‎6a2x＋‎10a2－a4＝0，‎ 由题意易知Δ＝‎36a4－4(‎2a2－1)(‎10a2－a4)≥0，‎ 解得a≥，所以e＝＝≤，‎ 所以e的最大值为.‎ ‎4．(方向3)已知点F1，F2分别是椭圆＋＝1的左、右焦点，点M是该椭圆上的一个动点，那么|＋|的最小值是(　C　)‎ A．4　　　　B．‎6 C．8　　　　D．10‎ 解析：设M(x0，y0)，F1(－3,0)，F2(3,0)．‎ 则＝(－3－x0，－y0)，＝(3－x0，－y0)，‎ 所以＋＝(－2x0，－2y0)，‎ ‎|＋|＝ ‎＝＝，‎ 因为点M在椭圆上，所以0≤y≤16，‎ 所以当y＝16时，|＋|取最小值为8.‎