高中数学必修2空间几何体考点

高中数学必修2空间几何体考点

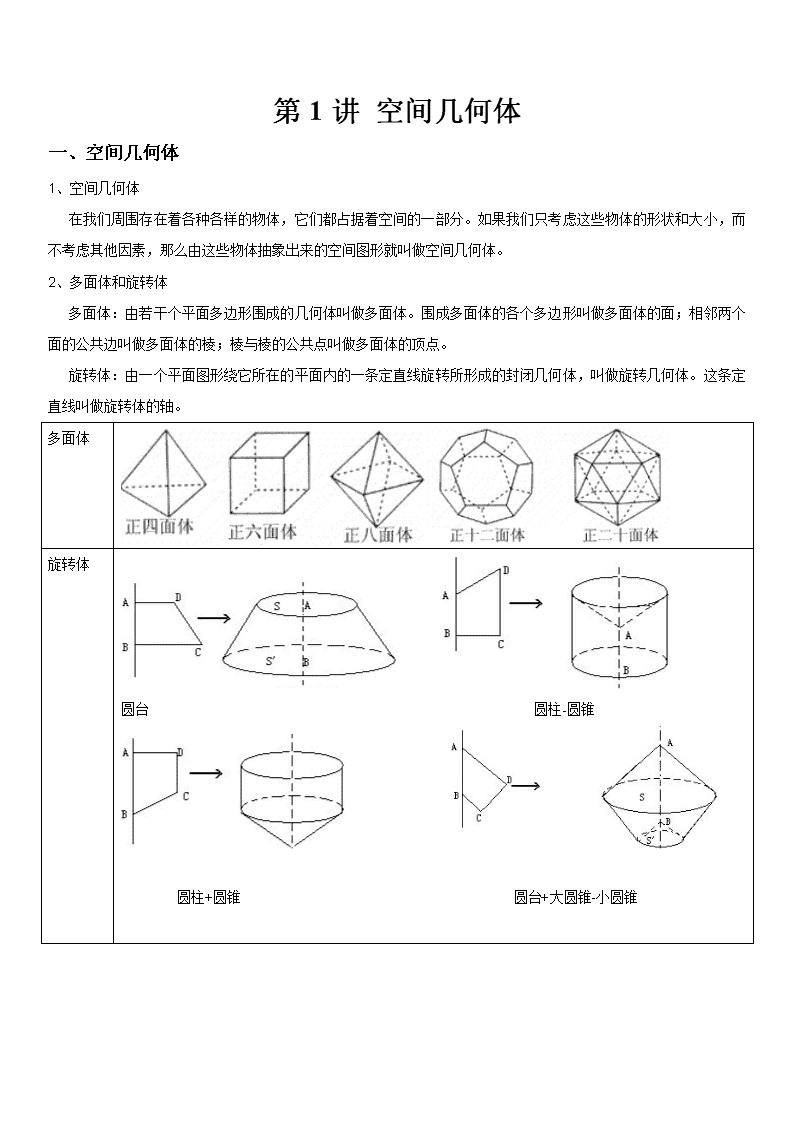
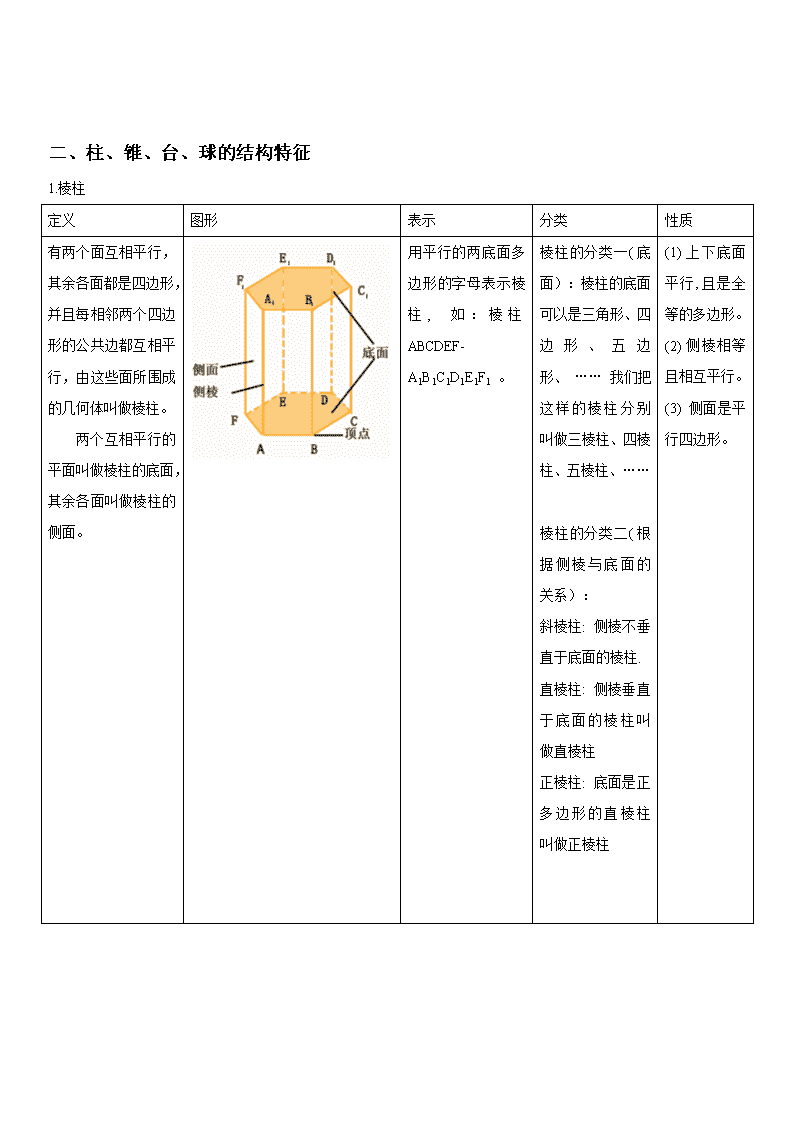
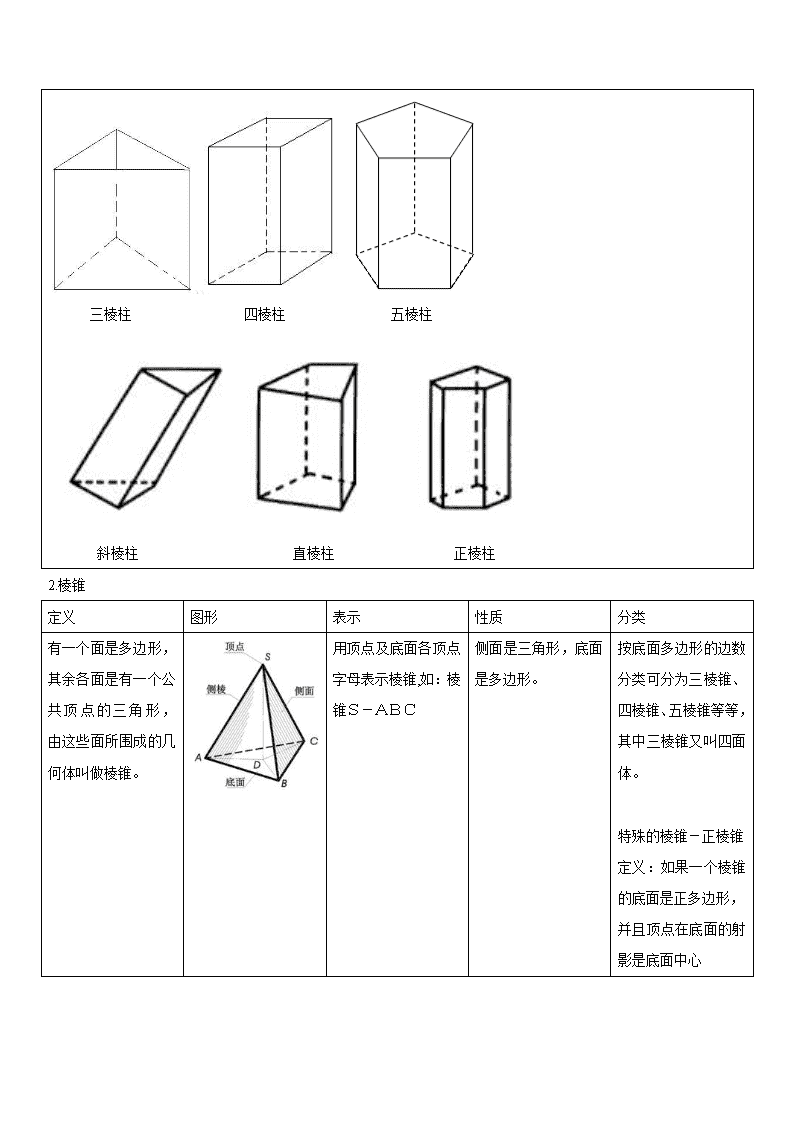
第 1 讲 空间几何体 一、空间几何体 1、空间几何体 在我们周围存在着各种各样的物体，它们都占据着空间的一部分。如果我们只考虑这些物体的形状和大小，而 不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体。 2、多面体和旋转体 多面体：由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面；相邻两个 面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点。 旋转体：由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体，叫做旋转几何体。这条定 直线叫做旋转体的轴。 多面体 旋转体 圆台 圆柱-圆锥 圆柱+圆锥 圆台+大圆锥-小圆锥 二、柱、锥、台、球的结构特征 1.棱柱 定义 图形 表示 分类 性质 有两个面互相平行， 其余各面都是四边 形，并且每相邻两个 四边形的公共边都互 相平行，由这些面所 围成的几何体叫做棱 柱。 两个互相平行的 平面叫做棱柱的底 面，其余各面叫做棱 柱的侧面。 用平行的两底面多 边形的字母表示棱 柱 , 如 ： 棱 柱 ABCDEF- A1B1C1D1E1F1 。 棱柱的分类一(底 面）：棱柱的底面 可以是三角形、四 边 形 、 五 边 形、 …… 我们把 这样的棱柱分别 叫做三棱柱、四棱 柱、五棱柱、…… 棱柱的分类二(根 据侧棱与底面的 关系）： 斜棱柱: 侧棱不垂 直于底面的棱柱. 直棱柱: 侧棱垂直 于底面的棱柱叫 做直棱柱 正棱柱: 底面是正 多边形的直棱柱 叫做正棱柱 (1)上下底面 平行 ,且是全 等的多边形。 (2)侧棱相等 且相互平行。 (3) 侧面是平 行四边形。 三棱柱 四棱柱 五棱柱 斜棱柱 直棱柱 正棱柱 2.棱锥 定义 图形 表示 性质 分类 有一个面是多边形， 其余各面是有一个公 共顶点的三角形，由 这些面所围成的几何 体叫做棱锥。 用顶点及底面各顶点 字母表示棱锥,如：棱 锥Ｓ－ＡＢＣ 侧面是三角形，底面 是多边形。 按底面多边形的边数 分类可分为三棱锥、 四棱锥、五棱锥等等， 其中三棱锥又叫四面 体。 特殊的棱锥－正棱锥 定义：如果一个棱锥 的底面是正多边形， 并且顶点在底面的射 影是底面中心 三棱锥 四棱锥 五棱锥 直棱锥 2.棱台 定义 图形 表示 分类 性质 用一个平行 于棱锥底面 的平面去截 棱锥，底面 和截面之间 的部分叫做 棱台。 棱台用表示上、 下底面各顶点 的字母来表示， 如下图，棱台 ABCD-A1B1C1 D1 由三棱锥、四棱 锥、五棱锥…截 得的棱台，分别 叫做三棱台，四 棱台，五棱台… 特殊的棱锥－ 由正棱锥截得 的棱台叫正棱 台 上下底面平行， 其余各面是梯 形，且侧棱延长 后交于一点。 三棱台 四棱台 正棱台 3.棱柱 定义 图形 表示 性质 定义：以矩形的一边 所在直线为旋转轴， 其余三边旋转形成的 曲面所围成的几何体 叫做圆柱。 用表示它的轴的字母 表示，如圆柱 OO1。 4.圆锥 定义 图形 表示 性质 以直角三角形的一条直角 边所在直线为旋转轴，其余 两边旋转而成的曲面所围 成的几何体叫做圆锥。 用表示它的轴的字母表 示，如圆锥 SO。 6.圆台 定义 图形 表示 性质 用一个平行于圆锥底面的 平面去截圆锥，底面与截面 之间的部分，这样的几何体 叫做圆台。 用表示它的轴的字母表示，如圆 台 OO′ 7.球的结构特征 1、球的定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体叫做球体，简称球。 （1）半圆的半径叫做球的半径。 （2）半圆的圆心叫做球心。 （3）半圆的直径叫做球的直径。 2、球的表示：用表示球心的字母表示，如球 O 3、球的性质 （1）用一个平面去截球，截面是圆面；用一个平面去截球面，截线是圆。 大圆---截面过圆心，半径等于球半径；小圆---截面不过圆心。 （2）球心和截面的圆心的连线垂直于截面。 （3）球心到截面的距离 d与球的半径 R及截面的半径 r，有下面的关系： 2 2r R d  解题方法：将立体中相关问题转化为平面几何问题 棱锥内由某些线段组成的直角三角形，在计算有关问题时很重要，它是将立体中相关问题转化为平面几何问题 的根据，如图 2-7 中的△AOE，△AOC，△ACE 及△OCE．这四个直角三角形中，若知道 AE、AC、AO、OE、OC 及 CE 这六条线段中的若干条时，则可以通过这些直角三角形间的关系求出其他线段． 总结 三、空间几何体的三视图和直观图 1、中心投影与平行投影 2、三视图 正视图——从正面看到的图 侧视图——从左面看到的图 俯视图——从上面看到的图 画物体的三视图时，要符合如下原则: 位置：正视图 侧视图 俯视图 大小：长对正，高平齐，宽相等. 3、直观图-----斜二测画法 重点：用斜二测画法画水平放置的平面图形的直观图，步骤如下： ⑴ 在已知图形中取互相垂直的 x轴和 y轴，两轴相交于点 O. 画直观图时，把它们画对应的 x'轴与 y'轴，两 轴交于点 O' ，且使∠x'O'y' ＝45º（或 135º），它们确定的平面表示水平面. ⑵ 已知图形中平行于 x轴或 y轴的线段，在直观图中分别画成平行于 x'轴或 y'轴的线段； ⑶ 已知图形中平行于 x轴的线段，在直观图中保持原长度不变；平行于 y轴的线段，长度为原来的一半． 例 1 用斜二测画法画水平放置的正六边形的直观图. 说明：1. 保持平行关系不变． 2.水平长度保持不变；纵向长度取其一半． 例 3 用斜二测画法画长、宽、高分别是 4cm、3cm、2cm的长方体 ABCD-A'B'C'D'的直观图. 四、 空间几何体的表面积与体积 （一 ）空间几何体的表面积 1棱柱、棱锥的表面积： 各个面面积之和 2 圆柱的表面积 3 圆锥的表面积 2S rl r   4 圆台的表面积 2 2S rl r Rl R       5 球的表面积 24S R 6 扇形的面积公式 2 1 360 2 n RS lr   扇形 （其中 l表示弧长， r表示半径） 222 rrlS   （二）空间几何体的体积 1柱体的体积 V S h 底 2 锥体的体积 1 3 V S h 底 3 台体的体积 1 ) 3 V S S S S h   下 下上 上（ 4 球体的体积 34 3 V R 第二讲 点、直线、平面之间的位置关系 空间点、直线、平面之间的位置关系 一、平面 1、平面及其表示 2、平面的基本性质 ①公理 1： ②公理 2：不共线的三点确定一个平面 ③公理 3： 二、点与面、直线位置关系 1、点与平面有 2种位置关系 A l B l l A B            P l P l P            则 1 2 A B      、 、 1 2 A l B l    、 、 2、点与直线有 2种位置关系 三、空间中直线与直线之间的位置关系 1、异面直线 2、直线与直线的位置关系        相交 共面 平行 异面 3、公理 4和定理 公理 4： 定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。 4、求异面直线所成角的步骤： ①作：作平行线得到相交直线； ②证：证明作出的角即为所求的异面直线所成的角； ③构造三角形求出该角。 提示：1、作平行线常见方法有：直接平移，中位线，平行四边形。 2、异面直线所的角的范围是 。 1 3 1 2 2 3 l l l l l l        0 00 ,90  四、空间中直线与平面之间的位置关系 位置关系 公共点 有无数个公共点 有且只有一个公共点 没有公共点 符号表示 图形表示 五、空间中平面与平面之间的位置关系 位置关系 两个平面平行 两个平面相交 公共点 没有公共点 有一条公共直线 符号表示   a   图形表示 直线、平面平行的判定及其性质 一、线面平行 1、判定： a 直线 与平面 平行a 直线 与平面 相交a直线 在平面内 a  a a A  b a b b a            （线线平行，则线面平行） 2、性质： （线面平行，则线线平行） 二、面面平行 1、判定： （线面平行，则面面平行） 2、性质 1： （面面平行，则线面平行） 性质 2： m m          （面面平行，则线面平行） a a a b b             a b a b P a b                   a a b b                说明（1）判定直线与平面平行的方法： ①利用定义：证明直线与平面无公共点。 ②利用判定定理：从直线与直线平行等到直线与平面平行。 ③利用面面平行的性质：两个平面平行，则其中一个平面内的直线必平行于另一个平面。 （2）证明面面平行的常用方法 ①利用面面平行的定义：此法一般与反证法结合。 ②利用判定定理。 ③证明两个平面垂直于同一个平面。 ④证明两个平面同时平行于第三个平面。 三、线线平行、面面平行、面面平行间的关系 直线与平面垂直的判定及其性质 一、直线与平面所成的角 0 00 ,90     0 0- - 0 ,180l     二、二面角 三、线面垂直 1、判定： 2、性质 1： 3、性质 2： 四、面面垂直 ,PO AO PA l        证明过程 为 在平面 上的投影， 为直线 与平面 所成的角。 , , - - BO l AO l BOA l     证明过程 是二面角 的平面角。 a b a b A l l a l b               a a b b        a a b b        1、判定： 文字表达：一个平面过另一个平面的垂线，则这两个平面垂直。 2、性质： 说明：（1）判定直线与平面垂直的方法： ①利用定义（可用反证法）。 ②利用判定定理。 ③利用性质定理。 ④结合平行关系： （2）判定平面与平面垂直的方法： ①利用定义判断（证）二面角的平面角是直角。 ②利用平面与平面垂直的判定定理。 l l          AB AB AB CD               ,a b a b   