高考数学总复习 三角函数公式及推导

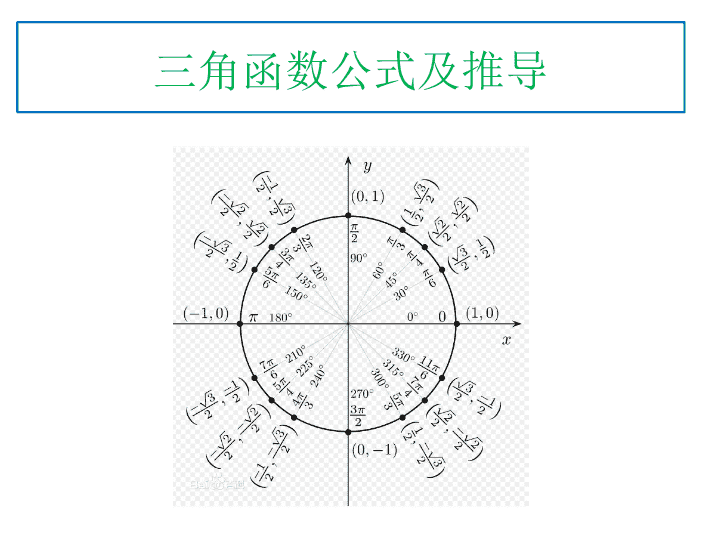
高考数学总复习 三角函数公式及推导

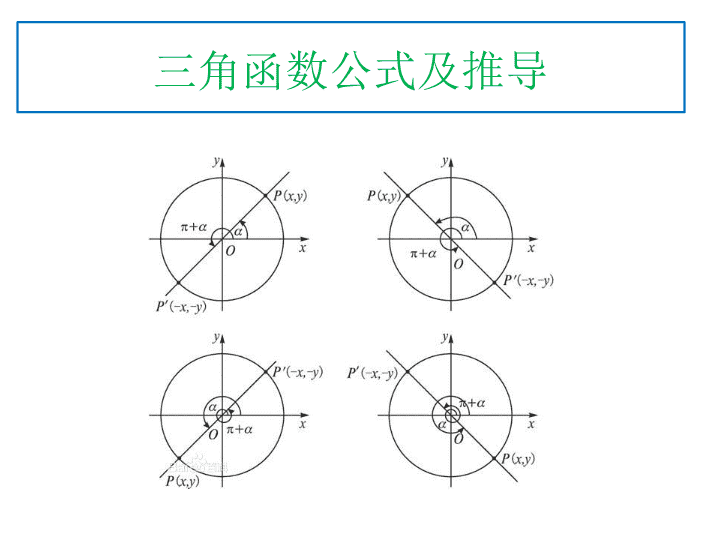
三角函数公式及推导 三角函数公式及推导 1----- 诱导公式（之一）： 常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα 公式三： 任意角α与 -α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα 1----- 诱导公式（之二）： 公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα 公式六 之一 ：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanα 公式六之二 sin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈z) ※ 规律总结 ※ 上面这些诱导公式可以概括为： 对于 k·π/2±α(k∈z) 的个三角函数值， ① 当 k 是偶数时，得到 α 的同名函数值，即函数名不改变； ② 当 k 是奇数时，得到 α 相应的余函数值，即 sin→cos;cos→sin;tan→cot,cot→tan. （奇变偶不变） 然后在前面加上把 α 看成锐角时原函数值的符号。 （符号看象限） 上述的记忆口诀是： 奇变偶不变，符号看象限。 公式右边的符号为把 α 视为锐角时，角 k·360°+α （ k∈z ）， -α 、 180°±α ， 360°-α 所在象限的原三角函数值的符号可记忆 水平诱导名不变；符号看象限。 各种三角函数在四个象限的符号如何判断，也可以记住口诀 “ 一全正；二正弦；三为切；四余弦 ” ． 这十二字口诀的意思就是说： 第一象限内任何一个角的四种三角函数值都是 “ ＋ ” ； 第二象限内只有正弦是 “ ＋ ” ，其余全部是 “ － ” ； 第三象限内切函数是 “ ＋ ” ，弦函数是 “ － ” ； 第四象限内只有余弦是 “ ＋ ” ，其余全部是 “ － ” ． 口诀总结 公式七： 额外的定义 （也是重要的呀） 2--- 同角三角函数基本关系 ⒈同角三角函数的基本关系式 倒数关系:tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1 商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα 平方关系：sin^2(α)＋cos^2(α)＝11＋tan^2(α)＝sec^2(α)1＋cot^2(α)＝csc^2(α) 证明： 同角三角函数关系六角形记忆法 六角形记忆法：（参看图片或参考资料链接） 构造以 “ 上弦、中切、下割；左正、右余、中间 1” 的正六边形为模型。 （ 1 ）倒数关系：对角线上两个函数互为倒数； （ 2 ）商数关系：六边形任意一顶点上的函数值等于与它相邻 的两个顶点上函数值的乘积。（主要是两条虚线两端的 三角函数值的乘积）。由此，可得商数关系式。 （ 3 ）平方关系：在带有阴影线的三角形中，上面两个顶点上 的三角函数值的平方和等于下面顶点上的三角函数值的 平方。 3--- 两角和差公式 两角和与差的三角函数公式sin（α＋β）＝sinαcosβ＋cosαsinβsin（α－β）＝sinαcosβ－cosαsinβcos（α＋β）＝cosαcosβ－sinαsinβcos（α－β）＝cosαcosβ＋sinαsinβ                 tanα＋tanβtan（α＋β）＝——————--              1－tanα ·tanβ                  tanα－tanβtan（α－β）＝——————              1＋tanα ·tanβ （ 和差公式的证明 ） 两角差的余弦 令 AO=BO=r 点的横坐标为 点 A 纵坐标为 点 B 的坐标为 两式相等，化简（或对照得）： y A B （O） C x β (α- β ） α 由余弦定理得： 两角和的余弦 两角和的正弦 两角差的正弦 两角和的正切 两角差的正切 由两角差的余弦得 4--- 二倍角公式 二倍角的正弦、余弦和正切公式（也称为：升幂缩角公式） 正弦的二倍角公式： 表示一： sin2α ＝ 2sinαcosα 证明：因为 sin(  +  )=sin  cos  +cos  sin  ，令  =  =  ， 所以， 可 得： sin2  =2  sin  cos  表示二：（ 以正切表示二倍角 ） sin2  = 2tan  1+tn 2  證明： sin2  =2sin  cos  =2 (sin  /cos ) . cos 2  =2tan / (sec 2  ) = 2tan /(1+tan 2  ) 余弦二倍角公式： 表示一： cos2 =cos 2  sin 2  =2cos 2  1=1  2sin 2  证明：因为 由和角公式： cos(  +  )=cos  cos  sin  sin  ， 令  =  =  所以，可得： cos2 =cos 2  sin 2  =2cos 2  1=1  2sin 2  表示二： cos2  = 1-tan 2  1+tan 2  證明：cos2  =2cos 2  1 = (2/sec 2 ) 1 =2/(1+tan 2 )  1 =(1-tan 2 ) /(1+tan 2 )           2tanα tan2α ＝ —————         1 － tan 2 α 证明：因为 由和角公式： tan(  +  )= (tan  +tan  )/(1-tan α.tan  ) ， 令 =  =  ， 所以，可得： 2tanα tan2α ＝ —————         1 － tan 2 α 正切的二倍角公式 結論：利用 tan  可以將 sin2 ， cos2 ， tan2 表示出來， 整理如下： (a) sin2  = 2tan /(1+ tan 2 ) (b) cos2 =(1- tan 2 )/ (1+tan 2 ) (c) tan2 =2tan  / (1- tan 2 ) 用三角形直观表示如下：（图） 6--- 半角公式 半角的正弦、余弦和正切公式（也称：降幂扩角公式） 或也可表示为：              1 － cosα sin^2(α/2) ＝ —————              2                1 ＋ cosα cos^2(α/2) ＝ —————                2                1 － cosα tan^2(α/2) ＝ —————              1 ＋ cosα 7--- 万能公式 万能公式推导 附推导：sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*，（因为cos^2(α)+sin^2(α)=1）再把*分式上下同除cos^2(α)，可得sin2α＝tan2α/(1＋tan^2(α))然后用α/2代替α即可。 同理可推导余弦的万能公式。正切的万能公式可通过正弦比余弦得到。 8---三倍角公式 三倍角的正弦、余弦和正切公式 (a)sin3  = 3sin   4sin 3  證明： sin3 =sin(  +2  )=sin  cos2  +cos  sin2  =sin (1  2sin 2  )+cos  (2sin  cos  ) = sin (1  2sin 2  )+2sin  cos 2  = sin (1  2sin 2  )+2sin  (1  sin 2  ) = 3sin  4sin 3  (b)cos3  =4cos 3   3cos  證明： cos3  =cos(  +2  )=cos  cos2  sin  sin2  =cos  (2cos 2  1)  sin  (2sin  cos  ) = cos  (2cos 2  1)  2sin 2  cos  = cos  (2cos 2  1)  2(1  cos 2  )cos  =4cos 3   3cos  三倍角的正切公式 因为： sin3α＝3sinα－4sin^3(α) cos3α＝4cos^3(α)－3cosα        3tanα－tan 3 α 所以： tan3α＝ ——————        1－3tan 2 α 三倍角公式推导 正切三倍角公式推导：（证明） tan3α＝sin3α/cos3α＝(sin2αcosα＋cos2αsinα)/(cos2αcosα-sin2αsinα)＝(2sinαcos^2(α)＋cos^2(α)sinα－sin^3(α))/(cos^3(α)－cosαsin^2(α)－2sin^2(α)cosα) 上下同除以cos^3(α)，得：tan3α＝(3tanα－tan^3(α))/(1-3tan^2(α)) 正弦三倍角公式推导 （证明） sin3α＝sin(2α＋α)＝sin2αcosα＋cos2αsinα＝2sinαcos^2(α)＋(1－2sin^2(α))sinα＝2sinα－2sin^3(α)＋sinα－2sin^2(α)＝3sinα－4sin^3(α) 余弦三倍角公式推导：（证明） cos3α＝cos(2α＋α)＝cos2αcosα－sin2αsinα＝(2cos^2(α)－1)cosα－2cosαsin^2(α)＝2cos^3(α)－cosα＋(2cosα－2cos^3(α))＝4cos^3(α)－3cosα 三倍角公式联想记忆 记忆方法：谐音、联想 正弦三倍角： 3 元 减 4 元 3 角（欠债了 ( 被减成负数 ) ，所以要 “ 挣钱 ”( 音似 “ 正弦 ”) ） 余弦三倍角： 4 元 3 角 减 3 元（减完之后还有 “ 余 ” ） 注意函数名，即正弦的三倍角都用正弦表示，余弦的三倍角都用余弦表示。 9--- 积化和差公式 积化和差公式推导（ 之一） 附推导：首先,我们知道 sin(a+b)=sina*cosb+cosa*sinb,sin(a-b)=sina*cosb-cosa*sinb我们把两式相加就得到sin(a+b)+sin(a-b)=2sina*cosb所以,sina*cosb=(sin(a+b)+sin(a-b))/2同理,若把两式相减,就得到cosa*sinb=(sin(a+b)-sin(a-b))/2同样的,我们还知道 cos(a+b)=cosa*cosb-sina*sinb,cos(a-b)=cosa*cosb+sina*sinb所以,把两式相加,我们就可以得到 cos(a+b)+cos(a-b)=2cosa*cosb所以我们就得到,cosa*cosb=(cos(a+b)+cos(a-b))/2同理,两式相减我们就得到sina*sinb=-(cos(a+b)-cos(a-b))/2这样,我们就得到了积化和差的四个公式: sina*cosb=(sin(a+b)+sin(a-b))/2cosa*sinb=(sin(a+b)-sin(a-b))/2cosa*cosb=(cos(a+b)+cos(a-b))/2sina*sinb=-(cos(a+b)-cos(a-b))/2 积化和差推导（证明之二）： 10--- 和差化积公式 和差化积的公式推导： 好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.我们把上述四个公式中的a+b设为x,a-b 设为y,那么a=(x+y)/2,b=(x-y)/2把a,b分别用x,y表示就可以得到和差化积的四个公式: sinx+siny=2sin((x+y)/2)*cos((x-y)/2)sinx-siny=2cos((x+y)/2)*sin((x-y)/2)cosx+cosy=2cos((x+y)/2)*cos((x-y)/2)cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2) 11--- 辅助角公式 其中 的象限由 的符号确定。 12--- 任意三角形面积公式： C a b h d B c A 13--- 余弦定理： 任意三角形一角的余弦等于两邻边的平方和减对边的平方之差与两邻边积的两倍之比。 证明： （证完） 14--- 正弦定理 A c O B a C c 为 Δ ABC 外接圆的直径 , 同理 对边与对角正弦之比相等，且为外接圆的半径的两倍 15--- 海伦公式（任意三角形已知三边求面积） 证明 证毕（公式） a,b ,c 为三角形的三边，∠ A， ∠ B， ∠ C 为三边所对应的三个角 16--- 特殊的三角函数值（表） sin 0 1 cos 1 0 tan 0 1 N/A 17 ：其它一些恒等变换的有用公式：也必须熟记 (a)cos2  =cos 2  sin 2  =2cos 2  1=1  2sin 2  (b) cos  =2cos 2  1=1  2sin 2 (c) cos 2  = (1+cos2  )/2 ， sin 2  =（1-cos2  )/2 18 ：一些常用的高次方降次 --- 有用的公式： (a)sin 4  +cos 4  =(sin 2  +cos 2  ) 2  2sin 2  cos 2  =1  2sin 2  cos 2  (b)sin 6  +cos 6  =(sin 2  +cos 2  ) 3  3sin 2  cos 2  ( sin 2  +cos 2  )=1  3 sin 2  cos 2  (c)tan  +cot  = 1/sin  cos  = 2/sin2  (d)(sin  cos  ) 2 = sin 2  +cos 2  2sin  cos  =1  sin2 