【数学】2018届一轮复习人教A版抛物线学案

【数学】2018届一轮复习人教A版抛物线学案

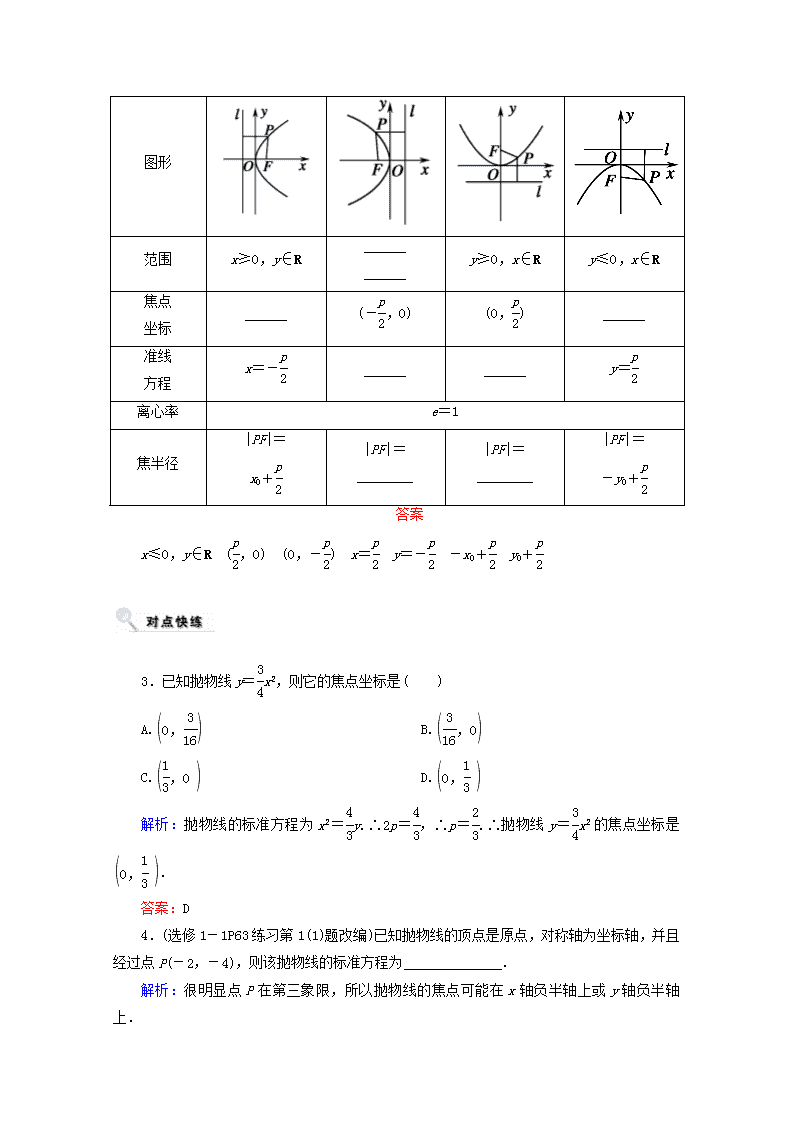
‎1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率)．‎ ‎2．理解数形结合的思想．‎ ‎3．了解抛物线的实际背景及抛物线的简单应用．‎ 知识点一　抛物线的定义 ‎ 平面内与一个定点F和一条定直线l(F∉l)距离______的点的轨迹叫做抛物线．‎ 答案 相等 ‎1．判断正误 ‎(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．(　　)‎ ‎(2)抛物线y2＝4x的焦点到准线的距离是4.(　　)‎ ‎(3)若一抛物线过点P(－2,3)，其标准方程可写为y2＝2px(p>0)．(　　)‎ 答案：(1)×　(2)×　(3)×‎ ‎2．(2016·浙江卷)若抛物线y2＝4x上的点M到焦点的距离为10，则M到y轴的距离是________．‎ 解析：由于抛物线y2＝4x的焦点为F(1,0)，准线为x＝－1，设点M的坐标为(x，y)，则x＋1＝10，所以x＝9.故M到y轴的距离是9.‎ 答案：9‎ 知识点二　抛物线的标准方程与几何性质 ‎ 标准 方程 y2＝2px ‎(p>0)‎ y2＝－2px ‎(p>0)‎ x2＝2py ‎(p>0)‎ x2＝－2py ‎(p>0)‎ 图形 范围 x≥0，y∈R ‎______‎ ‎______‎ y≥0，x∈R y≤0，x∈R 焦点 坐标 ‎______‎ ‎(－，0)‎ ‎(0，)‎ ‎______‎ 准线 方程 x＝－ ‎______‎ ‎______‎ y＝ 离心率 e＝1‎ 焦半径 ‎|PF|＝‎ x0＋ ‎|PF|＝‎ ‎________‎ ‎|PF|＝‎ ‎________‎ ‎|PF|＝‎ ‎－y0＋ 答案 x≤0，y∈R　(，0)　(0，－)　x＝　y＝－　－x0＋　y0＋ ‎3．已知抛物线y＝x2，则它的焦点坐标是(　　)‎ A. B. C. D. 解析：抛物线的标准方程为x2＝y.∴2p＝，∴p＝.∴抛物线y＝x2的焦点坐标是.‎ 答案：D ‎4．(选修1－1P63练习第1(1)题改编)已知抛物线的顶点是原点，对称轴为坐标轴，并且经过点P(－2，－4)，则该抛物线的标准方程为______________．‎ 解析：很明显点P在第三象限，所以抛物线的焦点可能在x轴负半轴上或y轴负半轴上．‎ 当焦点在x轴负半轴上时，设方程为y2＝－2px(p>0)，把点P(－2，－4)的坐标代入得(－4)2＝－2p×(－2)，解得p＝4，此时抛物线的标准方程为y2＝－8x；‎ 当焦点在y轴负半轴上时，设方程为x2＝－2py(p>0)，把点P(－2，－4)的坐标代入得(－2)2＝－2p×(－4)，解得p＝，此时抛物线的标准方程为x2＝－y.‎ 综上可知，抛物线的标准方程为y2＝－8x或x2＝－y.‎ 答案：y2＝－8x或x2＝－y ‎5．(2016·新课标全国卷Ⅱ)设F为抛物线C：y2＝4x的焦点，曲线y＝(k>0)与C交于点P，PF⊥x轴，则k＝(　　)‎ A. B．1‎ C. D．2‎ 解析：易知抛物线的焦点为F(1,0)，设P(xP，yP)，由PF⊥x轴可得xP＝1，代入抛物线方程得yP＝2(－2舍去)，把P(1,2)代入曲线y＝(k>0)得k＝2.‎ 答案：D 热点一　抛物线的定义及应用 ‎ ‎【例1】　已知抛物线y2＝2x的焦点是F，点P是抛物线上的动点，又有点A(3,2)，求|PA|＋|PF|的最小值，并求出取最小值时点P的坐标．‎ ‎【解】　将x＝3代入抛物线方程y2＝2x，得y＝±.∵>2，∴A在抛物线内部，如图．‎ 设抛物线上点P到准线l：x＝－的距离为d，由定义知|PA|＋|PF|＝|PA|＋d，当PA⊥l时，|PA|＋d最小，最小值为，即|PA|＋|PF|的最小值为，此时P点纵坐标为2，代入y2＝2x ‎，得x＝2，∴点P的坐标为(2,2)．‎ 将本例中点A的坐标改为(3,4)，求|PA|＋|PF|的最小值．‎ 解：当P、A、F共线时，|PA|＋|PF|最小，|PA|＋|PF|‎ ‎≥|AF|＝＝＝.‎ ‎【总结反思】‎ 与抛物线有关的最值问题，一般情况下都与抛物线的定义有关．由于抛物线的定义在运用上有较大的灵活性，因此此类问题也有一定的难度．“看到准线想焦点，看到焦点想准线”，这是解决抛物线焦点弦有关问题的重要途径.‎ ‎ ‎ ‎(2017·邢台摸底)已知M是抛物线x2＝4y上一点，F为其焦点，点A在圆C：(x＋1)2＋(y－5)2＝1上，则|MA|＋|MF|的最小值是________．‎ 解析：依题意，由点M向抛物线x2＝4y的准线l：y＝－1引垂线，垂足为M1，则有|MA|＋|MF|＝|MA|＋|MM1|，结合图形可知|MA|＋|MM1|的最小值等于圆心C(－1,5)到y＝－1的距离再减去圆C的半径，即等于6－1＝5，因此|MA|＋|MF|的最小值是5.‎ 答案：5‎ 热点二　抛物线的标准方程及几何性质 ‎ ‎【例2】　(1)(2017·泉州模拟)如图，过抛物线y2＝2px(p>0)的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程为(　　)‎ A．y2＝x　　　　B．y2＝3x C．y2＝x　　　　D．y2＝9x ‎(2)若双曲线C：2x2－y2＝m(m>0)与抛物线y2＝16x的准线交于A，B两点，且|AB ‎|＝4，则m的值是__________．‎ ‎【解析】　(1)如图，分别过点A，B作准线的垂线，分别交准线于点E，D，‎ 设|BF|＝a，则由已知得：|BC|＝‎2a，‎ 由定义得：|BD|＝a，故∠BCD＝30°，‎ 在直角三角形ACE中，因为|AF|＝3，|AC|‎ ‎＝3＋‎3a，又2|AE|＝|AC|，所以3＋‎3a＝6，从而得a＝1，因为BD∥FG，所以＝，求得p＝，因此抛物线方程为y2＝3x.‎ ‎(2)y2＝16x的准线l：x＝－4，因为C与抛物线y2＝16x的准线l：x＝－4交于A，B两点，|AB|＝4，所以A(－4,2)，B(－4，－2)，将A点坐标代入双曲线方程得2(－4)2－(±2)2＝m，所以m＝20.‎ ‎【答案】　(1)B　(2)20‎ ‎【总结反思】‎ ‎1．求抛物线的标准方程的方法 ‎(1)先定位：根据焦点或准线的位置．‎ ‎(2)再定形：即根据条件求p.‎ ‎2．抛物线性质的应用技巧 ‎(1)利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程．‎ ‎(2)要结合图形分析，灵活运用平面图形的性质以形助数.‎ ‎ ‎ ‎(1)以双曲线－y2＝1的左焦点为焦点，顶点在原点的抛物线方程是(　　)‎ A．y2＝4x B．y2＝－4x C．y2＝－4x D．y2＝－8x ‎(2)(2016·新课标全国卷Ⅰ)以抛物线C的顶点为圆心的圆交C于A，B两点，交C 的准线于D，E两点．已知|AB|＝4，|DE|＝2，则C的焦点到准线的距离为(　　)‎ A．2 B．4‎ C．6 D．8‎ 解析：(1)由题意知抛物线的焦点为(－2,0)，又顶点在原点，所以抛物线的方程为y2＝－8x.‎ ‎(2)由题意，不妨设抛物线方程为y2＝2px(p>0)，由|AB|＝4，|DE|＝2，可取A(，2)，D(－，)．设O为坐标原点，由|OA|＝|OD|，得＋8＝＋5，得p＝4，所以选B.‎ 答案：(1)D　(2)B 热点三　直线与抛物线的位置关系 ‎ 考向1　焦点弦问题 ‎【例3】　已知过抛物线y2＝2px(p>0)的焦点，斜率为2的直线交抛物线于A(x1，y1)，B(x2，y2)(x10)的焦点为F(0,1)，过点F作直线l交抛物线C于A，B两点．椭圆E的中心在原点，焦点在x轴上，点F是它的一个顶点，且其离心率e＝.‎ ‎(1)分别求抛物线C和椭圆E的方程；‎ ‎(2)经过A，B两点分别作抛物线C的切线l1，l2，切线l1与l2相交于点M.证明AB⊥MF.‎ ‎【解】　(1)由抛物线C：x2＝2py(p>0)的焦点为F(0,1)可得抛物线C的方程为x2＝4y ‎.设椭圆E的方程为＋＝1(a>b>0)，半焦距为c，由已知可得解得a＝2，b＝1.所以椭圆E的方程为＋y2＝1.‎ ‎(2)证明：显然直线l的斜率存在，否则直线l与抛物线C只有一个交点，不符合题意，故可设直线l的方程为y＝kx＋1，A(x1，y1)，B(x2，y2)(x1≠x2)，由消去y并整理得x2－4kx－4＝0，∴x1x2＝－4.∵抛物线C的方程为y＝x2，∴y′＝x.∴直线l1，l2的方程分别是y－y1＝x1(x－x1)，y－y2＝x2(x－x2)，即y＝x1x－x，y＝x2x－x.联立直线l1，l2的方程，解得两条切线l1，l2的交点M的坐标为，即M.‎ ‎∴·＝·(x2－x1，y2－y1)＝(x－x)－2＝0.∴AB⊥MF.‎ ‎【总结反思】‎ 直线与圆锥曲线相交问题通常采用“设而不求”的方法．设交点坐标为(x1，y1)，(x2，y2)，直线方程为y＝kx＋b，代入圆锥曲线方程消去y得关于x的一元二次方程，由韦达定理得x1＋x2，x1x2，再把题中与交点有关的已知条件、要证明的结论等用x1，y1，x2，y2表示出来，最后把x1＋x2，x1x2代入转化变形可解决问题.‎ ‎ ‎ ‎(2017·陕西宝鸡质检)已知抛物线G的顶点在原点，焦点在y轴正半轴上，抛物线上的点P(m,4)到其焦点F的距离等于5.‎ ‎(1)求抛物线G的方程；‎ ‎(2)在正方形ABCD的三个顶点A(x1，y1)，B(x2，y2)，C(x3，y3)(x1<0≤x20，则直线BC的方程为y＝k(x－x2)＋(k>0)，由消y，得x2－4kx－x＋4kx2＝0，易知x2，x3为该方程的两个根，故有x2＋x3＝4k，得x3＝4k－x2，从而得|BC|＝(x3－x2)＝2(2k－x2)，类似地，直线AB的方程为y＝－(x－x2)＋，从而得|AB|＝(2＋kx2)，由|AB|＝|BC|，得k2·(2k－x2)＝(2＋kx2)，解得x2＝，|AB|＝|BC|＝(k>0)．因为≥＝4，所以SABCD ‎＝|AB|2≥32，即SABCD的最小值为32，当且仅当k＝1时取得最小值．‎ ‎1．认真区分四种形式的标准方程 ‎(1)区分y＝ax2与y2＝2px(p>0)，前者不是抛物线的标准方程．‎ ‎(2)求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y2＝mx或x2＝my(m≠0)．‎ ‎2．抛物线的离心率e＝1，体现了抛物线上的点到焦点的距离等于到准线的距离．因此，涉及抛物线的焦半径、焦点弦问题，可以优先考虑利用抛物线的定义转化为点到准线的距离，这样就可以使问题简化．‎ 抛物线上的点到焦点的距离根据定义转化为到准线的距离，即|PF|＝|x|＋或|PF|＝|y|＋.‎ 巧用定义妙解最值 ‎【例】　抛物线y2＝4mx(m>0)的焦点为F，点P为该抛物线上的动点，若点A(－m,0)，则的最小值为________．‎ ‎【分析】　设点P的坐标(xP，yP)，利用抛物线的定义，求出|PF|，再利用两点间的距离公式求出|PA|2，把()2用xP的代数式来表示，再利用基本不等式，即可求出的最小值．‎ ‎【解析】　设点P的坐标为(xP，yP)，由抛物线的定义，知 ‎|PF|＝xP＋m，又|PA|2＝(xP＋m)2＋y＝(xP＋m)2＋4mxP，所以()2＝＝≥＝(当且仅当xP＝m时取等号)，所以≥，所以的最小值为.‎ ‎【答案】　 解题策略：破解抛物线上的动点与焦点、动点与定点的距离比的最值问题需过好三关：一是“定义关”，把抛物线上的动点到焦点的距离转化为抛物线上的动点到准线的距离；二是“公式关”，即应用两点间的距离公式，求动点与定点的距离；三是“最值关”，需熟练掌握配方法、导数法、换元法、基本不等式等求最值.‎ ‎ ‎ 已知点P是抛物线y2＝2x上的动点，B(－1,1)，点P到直线l：x＝－的距离为d，求d＋|PB|的最小值．‎ 解：由题意得抛物线y2＝2x的焦点F(，0)，直线l是抛物线的准线，如下图，连接BF，PF，所以d＝|PF|，则d＋|PB|‎ ‎＝|PF|＋|PB|≥|BF|＝＝，当且仅当B，P，F三点共线时取等号，所以d＋|PB|的最小值为.‎