高中数学北师大版新教材必修一同步课件：阶段提升课 第六课　概率

高中数学北师大版新教材必修一同步课件：阶段提升课 第六课　概率

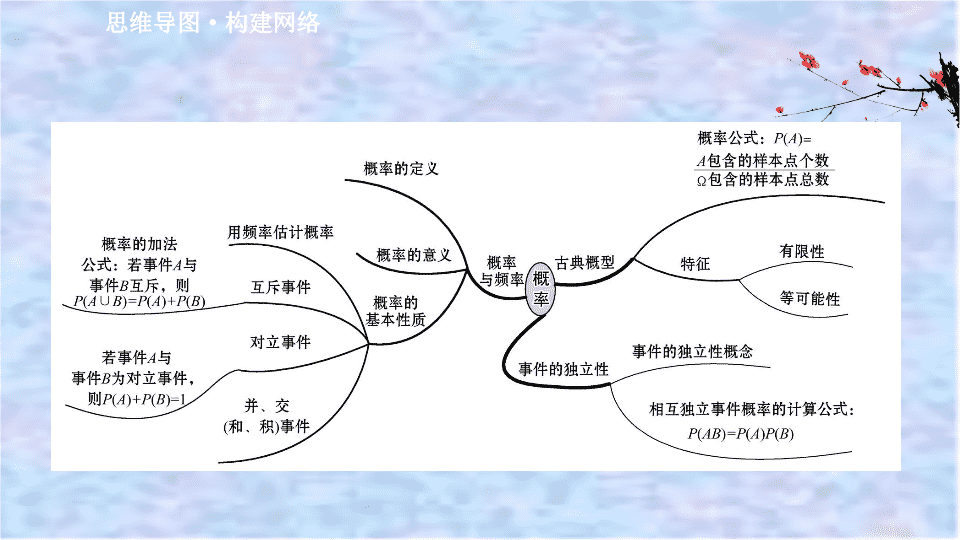
阶段提升课 第六课　概　　率 思维导图 · 构建网络 考点整合 · 素养提升 题组训练一　互斥事件与对立事件  1. 黄种人群中各种血型的人所占的比例如表 : 血型 A B AB O 该血型的人所占比例 (%) 28 29 8 35 已知同种血型的人可以输血 ,O 型血可以输给任一种血型的人 , 其他不同血型的人不能互相输血 , 张三是 B 型血 , 若张三因病需要输血 , 问 : (1) 任找一个人 , 其血可以输给张三的概率是多少 ? (2) 任找一个人 , 其血不能输给张三的概率是多少 ? 【 解析 】 (1) 对任意一人 , 其血型为 A,B,AB,O 的事件分别记为 A′,B′,C′,D′, 由已知 , 有 P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35, 因为 B,O 型血 可以输给张三 , 所以 “ 任找一人 , 其血可以输给张三 ” 为事件 B′∪D′. 依据互 斥事件的概率加法公式 , 有 P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64. (2) 方法一 : 由于 A,AB 型血不能输给 B 型血的人 , 所以 “ 任找一人 , 其血不能输给 张三 ” 为事件 A′∪C′, 依据互斥事件的概率加法公式 , 有 P(A′∪C′)=P(A′)+P(C′)=0.28+0.08=0.36. 方法二 : 因为事件 “ 任找一人 , 其血可以输给张三 ” 与事件 “ 任找一人 , 其血不 能输给张三 ” 是对立事件 , 所以由对立事件的概率公式 , 有 P(A′∪C′)=1- P(B′∪D′)=1-0.64=0.36. 2. 某商场有奖销售中 , 购满 100 元商品得 1 张奖券 , 多购多得 .1 000 张奖券为一个开奖单位 , 设特等奖 1 个 , 一等奖 10 个 , 二等奖 50 个 . 设 1 张奖券中特等奖、一等奖、二等奖的事件分别为 A,B,C, 求 : (1)P(A),P(B),P(C); (2)1 张奖券的中奖概率 ; (3)1 张奖券不中特等奖且不中一等奖的概率 . 【 解析 】 (1)P(A)= ,P(B)= = ,P(C)= = . 故事件 A,B,C 的概率分别为 , , . (2)1 张奖券中奖包含中特等奖、一等奖、二等奖 . 设 “ 1 张奖券中奖 ” 这个事件为 M, 则 M=A∪B∪C. 因为 A,B,C 两两互斥 , 所以 P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)= . 故 1 张奖券的中奖概率为 . (3) 设 “ 1 张奖券不中特等奖且不中一等奖 ” 为事件 N, 则事件 N 与 “ 1 张奖券中特 等奖或中一等奖 ” 为对立事件 , 所以 P(N)=1-P(A∪B)= . 故 1 张奖券不中特等奖且不中一等奖的概率为 . 【 方法技巧 】 互斥事件、对立事件的概念与计算 (1) 互斥事件是不可能同时发生的两个事件 ; 对立事件除要求这两个事件不同时 发生外 , 还要求二者必须有一个发生 . 因此对立事件一定是互斥事件 , 但互斥事 件不一定是对立事件 , 对立事件是互斥事件的特殊情况 . (2) 若 A 1 ,A 2 ,…,A n 互斥 , 则 P(A 1 +A 2 +…+A n )=P(A 1 )+P(A 2 )+…+P(A n ). 对立事件概率 由公式可得 P(A)=1-P( )( 这里 是 A 的对立事件 ). 题组训练二　古典概型  1.“ 微信抢红包”自 2015 年以来异常火爆 , 在某个微信群某次进行的抢红包活 动中 , 若所发红包的总金额为 9 元 , 被随机分配为 1.49 元 ,1.31 元 ,2.19 元 ,3.40 元 ,0.61 元 , 共 5 份 , 供甲、乙等 5 人抢 , 每人只能抢一次 , 则甲、乙两人抢到的金 额之和不低于 4 元的概率为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A. B. C. D. 【 解析 】 选 B. 因为甲、乙两人从五份红包中随机取两份的可能情况有 10 种 , 其 中所抢到的金额之和大于等于 4 的情况有 (0.61,3.40),(1.49,3.40),(2.19,3.40),(1.31,3.40), 共 4 种 , 所以甲、乙两人 抢到的金额之和不低于 4 元的概率为 P= . 2. 从集合 A={2,4} 中随机抽取一个数记为 a, 从集合 B={1,3} 中随机抽取一个数记 为 b, 则 f(x)= ax 2 +bx+1 在 (-∞,-1] 上单调递减的概率为 ( 　　 ) A. B. C. D.0 【 解析 】 选 B.(a,b) 的所有取值情况如下 :(2,1),(2,3),(4,1),(4,3), 共 4 种 , 记 “ f(x) 在区间 (-∞,-1] 上单调递减 ” 为事件 A, 由条件知 f(x) 的图象开口一定向 上 , 对称轴为直线 x=- , 则 - ≥-1, 即 0< ≤1, 则事件 A 包含的情况如 下 :(2,1),(4,1),(4,3), 共 3 种 , 则 P(A)= . 3. 将一枚质地均匀的骰子 ( 一种各个面上分别标有 1,2,3,4,5,6 个点的正方体玩 具 ) 先后抛掷 2 次 , 则出现向上的点数之和小于 10 的概率为 　　　　 .  【 解析 】 将一枚质地均匀的骰子先后抛掷 2 次 , 所有等可能的结果有 (1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2), … ,(6,6), 共 36 种情况 . 设事件 A= “ 出现向上的点数之和小于 10 ” , 其对立事件 = “ 出现向上的点数之 和大于或等于 10 ” , 包含的可能结果有 (4,6),(5,5),(5,6),(6,4),(6,5),(6,6), 共 6 种情况 . 所以由古典概型的概率公式 , 得 P( )= = , 所以 P(A)=1- = . 答案 : 4. 有 7 位歌手 (1 至 7 号 ) 参加一场歌唱比赛 , 由 500 名大众评委现场投票决定歌手名次 , 根据年龄将大众评委分为五组 , 各组的人数如表 : 组别 A B C D E 人数 50 100 150 150 50 (1) 为了调查大众评委对 7 位歌手的支持情况 , 现用分层随机抽样方法从各组中抽取若干名大众评委 , 其中从 B 组中抽取了 6 人 . 请将其余各组抽取的人数填入表中 . (2) 在 (1) 中 , 若 A,B 两组被抽到的大众评委中各有 2 人支持 1 号歌手 , 现从这两组被抽到的大众评委中分别任选 1 人 , 求这 2 人都支持 1 号歌手的概率 . 组别 A B C D E 人数 50 100 150 150 50 抽取人数 6 【 解析 】 (1) 由题设知 , 分层抽样的抽取比例为 6%, 所以各组抽取的人数如表 : 组别 A B C D E 人数 50 100 150 150 50 抽取人数 3 6 9 9 3 (2) 记从 A 组抽到的 3 个评委为 a 1 ,a 2 ,a 3 , 其中 a 1 ,a 2 支持 1 号歌手 ; 从 B 组抽到的 6 个 评委为 b 1 ,b 2 ,b 3 ,b 4 ,b 5 ,b 6 , 其中 b 1 ,b 2 支持 1 号歌手 . 从 {a 1 ,a 2 ,a 3 } 和 {b 1 ,b 2 ,b 3 ,b 4 ,b 5 ,b 6 } 中各抽取 1 人的所有结果为 由树状图知所有结果共 18 种 , 其中 2 人都支持 1 号歌手的有 a 1 b 1 ,a 1 b 2 ,a 2 b 1 ,a 2 b 2 共 4 种 , 故所求概率 . 5. 某校高三学生体检后 , 为了解高三学生的视力情况 , 该校从高三六个班的 300 名学生中以班为单位 ( 每班学生 50 人 ), 每班按随机抽样方法抽取了 8 名学生的视 力数据 . 其中高三 (1) 班抽取的 8 名学生的视力数据与人数见表 : 视力 数据 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2 5.3 人数 2 2 2 1 1 (1) 用上述样本数据估计高三 (1) 班学生视力的平均值 ; (2) 已知其余五个班学生视力的平均值分别为 4.3,4.4,4.5,4.6,4.8. 若从这六 个班中任意抽取两个班学生视力的平均值作比较 , 求抽取的两个班学生视力的 平均值之差的绝对值不小于 0.2 的概率 . 【 解析 】 (1) 高三 (1) 班学生视力的平均值为 , 故用上述样本数据估计高三 (1) 班学生视力的平均值为 4.7. (2) 从这六个班中任意抽取两个班学生视力的平均值作比较 , 所有的取法共有 15 种 , 而满足抽取的两个班学生视力的平均值之差的绝对值不小于 0.2 的取法 有 :(4.3,4.5),(4.3,4.6),(4.3,4.7),(4.3,4.8),(4.4,4.6),(4.4,4.7),(4.4 ,4.8),(4.5,4.7),(4.5,4.8),(4.6,4.8), 共有 10 种 , 故抽取的两个班学生视力的平均值之差的绝对值不小于 0.2 的概率为 . 【 方法技巧 】 古典概型概率的计算 (1) 古典概型是一种最基本的概率模型 , 也是学习其他概率模型的基础 , 在高考 题中 , 经常出现此种概率模型的题目 . 解题时要紧紧抓住古典概型的两个基本特 征 , 即有限性和等可能性 . (2) 在应用公式 P(A)= 时 , 关键是正确理解试验的发生过程 , 求出试验的样本空 间的样本点总数 n 和事件 A 的样本点个数 m. 题组训练三　频率和概率  1. 某射击运动员为备战下届奥运会 , 在相同条件下进行射击训练 , 结果如表 : 射击次数 n 10 20 50 100 200 500 击中靶心 次数 m 8 19 44 92 178 455 击中靶心 的频率 0.8 0.95 0.88 0.92 0.89 0.91 (1) 该射击运动员射击一次 , 击中靶心的概率大约是多少 ? (2) 假设该射击运动员射击了 300 次 , 则击中靶心的次数大约是多少 ? (3) 假如该射击运动员射击了 300 次 , 前 270 次都击中靶心 , 那么后 30 次一定都击不中靶心吗 ? 【 解析 】 (1) 由题意得 , 击中靶心的频率与 0.9 接近 , 故概率约为 0.9. (2) 击中靶心的次数大约为 300×0.9=270( 次 ). (3) 由概率的意义 , 可知概率是个常数 , 不因试验次数的变化而变化 . 后 30 次中 , 每次击中靶心的概率仍约为 0.9, 所以不一定击不中靶心 . 2. 对一批优盘进行抽检 , 结果如表 : 抽出件数 a 50 100 200 300 400 500 次品件数 b 3 4 5 6 8 9 次品频率 (1) 计算表中次品的频率 ; (2) 从这批优盘中任抽一个是次品的概率约是多少 ? (3) 为保证买到次品的顾客能够及时更换 , 要销售 2 000 个优盘 , 至少需进货多少个优盘 ? 【 解析 】 (1) 表中次品频率从左到右依次为 0.06,0.04,0.025,0.02,0.02,0.018. (2) 当抽取件数 a 越来越大时 , 出现次品的频率在 0.02 附近摆动 , 所以从这批优盘 中任抽一个是次品的概率约是 0.02. (3) 设需要进货 x 个优盘 , 为保证其中有 2 000 个正品优盘 , 则 x(1-0.02)≥2 000, 因为 x 是正整数 , 所以 x≥2 041, 即至少需进货 2 041 个优盘 . 【 方法技巧 】 对于概率的定义应注意以下几点 (1) 求一个事件的概率的基本方法是通过大量的重复试验 . (2) 只有当频率在某个常数附近摆动时 , 这个常数才叫作事件 A 的概率 . (3) 概率是频率的稳定值 , 而频率是概率的近似值 . (4) 概率反映了随机事件发生的可能性的大小 . (5) 必然事件的概率为 1, 不可能事件的概率为 0, 故 0≤P(A)≤1. 题组训练四　事件的独立性  1. 抛掷两枚质地均匀的硬币 ,A={ 第一枚为正面向上 },B={ 第二枚为正面向上 }, 则事件 C={ 两枚向上的面为一正一反 } 的概率为 ( 　　 ) A.0.25 B.0.5 C.0.75 D.0.375 【 解析 】 选 B.P(A)=P(B)= ,P( )=P( )= . 因为事件 A, ,B, 相互独立 , 所以 P(C)=P(A + B)=P(A)P( )+P( )P(B)= × + × =0.5. 2. 一场 5 局 3 胜制的乒乓球对抗赛 , 当甲运动员先胜 2 局时 , 比赛因故中断 . 已知 甲、乙水平相当 , 每局甲胜的概率都为 , 则这场比赛的奖金分配 ( 甲∶乙 ) 应为 ( 　　 ) A.6∶1 B.7∶1 C.3∶1 D.4∶1 【 解析 】 选 B. 奖金分配比即为甲乙取胜的概率比 . 甲前两局已胜 , 甲胜有 3 种情 况 :① 甲第三局胜记为 A 1 ,P(A 1 )= ,② 甲第三局负第四局胜为 A 2 ,P(A 2 )= × = ,③ 第三局、第四局甲负 , 第五局甲胜为 A 3 ,P(A 3 )= × × = . 所以甲胜 的概率 P=P(A 1 )+P(A 2 )+P(A 3 )= , 乙胜的概率则为 . 故甲∶乙 =7∶1. 3. 假设有 5 个条件很类似的女孩 , 把她们分别记为 A,C,J,K,S. 她们应聘秘书工作 , 但只有 3 个秘书职位 , 因此 5 人中仅有三人被录用 . 如果 5 个人被录用的机会相等 , 分别计算下列事件的概率 : ① 女孩 K 得到一个职位 ; ② 女孩 K 和 S 各自得到一个职位 ; ③ 女孩 K 或 S 得到一个职位 . 【 解析 】 5 人中有 3 人被录用 , 共有 :ACJ,ACK,ACS,AJK,AJS,AKS,CJK,CJS,CKS,JKS,10 种结果 , 由古典概型知 : ① 女孩 K 得到一个职位的概率为 :P 1 = ; ② 女孩 K 和 S 各自得到一个职位的概率为 :P 2 = ; ③ 女孩 K 或 S 得到一个职位的概率为 :P 3 = . 【 方法技巧 】 相互独立事件的概率通常和互斥事件的概率综合在一起考查 , 这类问题具有一个明显的特征 , 那就是在题目的条件中已经出现一些概率值 , 解题时先要判断事件的性质 ( 是互斥还是相互独立 ), 再选择相应的公式计算求解 .