江西省九江市彭泽一中2019-2020学年高一上学期第一次月考数学试题

江西省九江市彭泽一中2019-2020学年高一上学期第一次月考数学试题

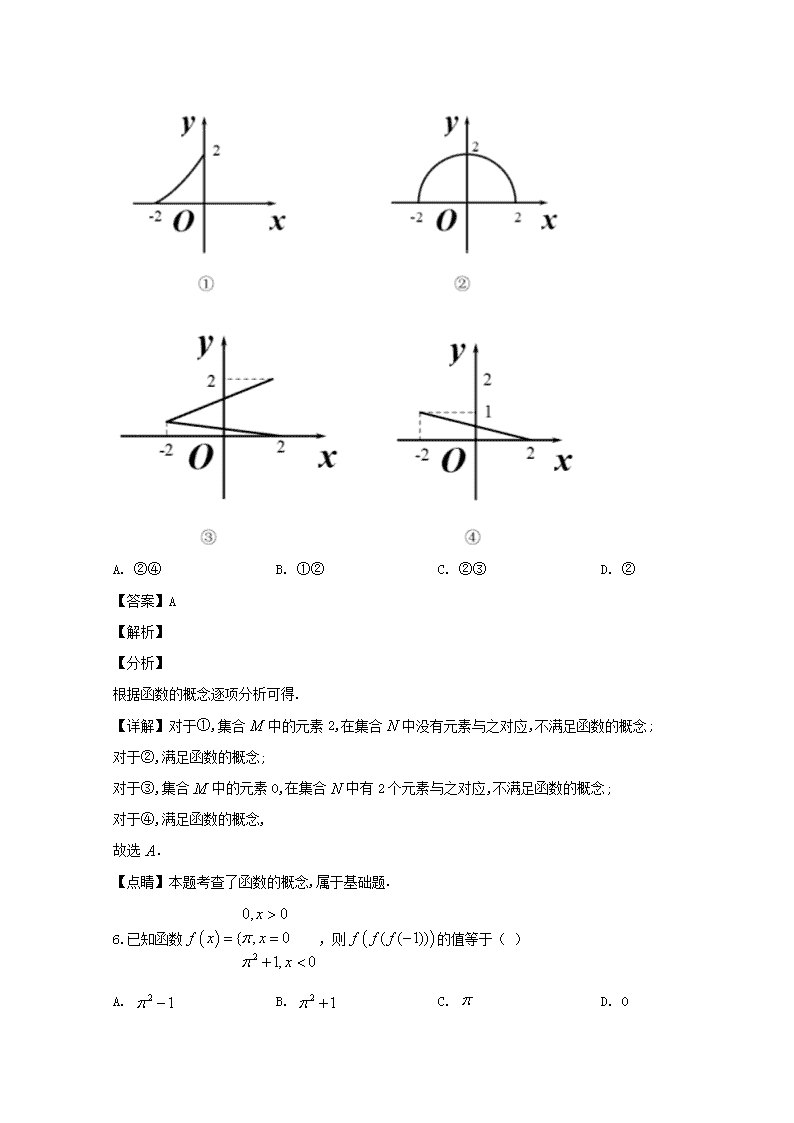
www.ks5u.com ‎2019~2020学年度上学期高一第一次月考数学试卷 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.下列选项能组成集合的是（ ）‎ A. 兴趣广泛的同学 B. 个子较高的男生 C. 英文26个字母 D. 非常大数 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据集合中元素的确定性,逐项分析可得.‎ ‎【详解】对于,兴趣广泛的标准不明确,不能组成集合;‎ 对于,个子较高的标准不明确,不能组成集合;‎ 对于,英文26个字母能组成集合;‎ 对于,非常大的标准不明确,不能组成集合.‎ 故选.‎ ‎【点睛】本题考查了集合中元素的确定性,属于基础题.‎ ‎2.已知,则下列写法正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据元素与集合是属于或不属于关系,集合与集合是包含或不包含关系逐项分析可得.‎ ‎【详解】对于,元素0和集合是属于关系;‎ 对于,集合与集合不是属于关系,是包含于关系;‎ 对于,空集与是真包含于关系,不是属于关系;‎ 对于,集合与集合是包含于关系.‎ 故选.‎ ‎【点睛】本题考查了元素与集合,集合与集合之间的关系,属于基础题.‎ ‎3.若集合=是包含-2的无限集，则a的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 将代入可解得.‎ ‎【详解】因为集合A=是包含-2的无限集,‎ 所以, 所以,所以.此时集合满足题意.‎ 故选.‎ ‎【点睛】本题考查了元素与集合的关系,属于基础题.‎ ‎4.已知集合=，=，，则等于（ ）‎ A. （1,2） B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 分析两个集合中元素的类型可得.‎ ‎【详解】因为集合数集,集合是点集,两个集合没有公共元素,‎ 所以两个集合的交集为空集.‎ 故选.‎ ‎【点睛】本题考查了集合的交集运算,属于基础题.‎ ‎5.已知集合=，集合=，下列能表示从集合到集合的函数的图像是（ ）‎ A. ②④ B. ①② C. ②③ D. ②‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据函数的概念逐项分析可得.‎ ‎【详解】对于①,集合中的元素2,在集合中没有元素与之对应,不满足函数的概念;‎ 对于②,满足函数的概念;‎ 对于③,集合中的元素0,在集合中有2个元素与之对应,不满足函数的概念;‎ 对于④,满足函数的概念,‎ 故选.‎ ‎【点睛】本题考查了函数的概念,属于基础题.‎ ‎6.已知函数，则的值等于（ ）‎ A. B. C. D. 0‎ ‎【答案】C ‎【解析】‎ 试题分析：‎ 考点：分段函数求值 ‎7.若函数的递增区间是，则等于（ ）‎ A. 6 B. 7 C. D. 5‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 通过分类讨论去绝对值将函数化成分段函数,可得函数的递增区间,与已知递增区间比较可得.‎ ‎【详解】因为函数 ,‎ 所以函数的递增区间是,‎ 结合已知可得,,所以.‎ 故选.‎ ‎【点睛】本题考查了函数的单调性,属于基础题.‎ ‎8.已知函数的定义域为，则函数的定义域为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由得,再由可解得.‎ ‎【详解】因为函数的定义域为,即,‎ 所以,‎ 所以函数的定义域为,‎ 由,得,‎ 所以函数的定义域为.‎ 故选.‎ ‎【点睛】本题考查了抽象函数的定义域,属于中档题.‎ 抽象函数定义域的四种类型:‎ 一、已知的定义域，求的定义域,‎ 其解法是：若的定义域为 ，则中，从中解得的取值范围即为的定义域。‎ 二、已知的定义域，求的定义域。‎ 其解法是：若的定义域为，则由确定的范围即为 的定义域。‎ 三、已知的定义域，求的定义域。‎ 其解法是：可先由定义域求得的定义域，再由的定义域求得的定义域。‎ 四、运算型的抽象函数 求由有限个抽象函数经四则运算得到的函数的定义域，其解法是：先求出各个函数的定义域，再求交集。‎ ‎9.已知集合满足，2，，2，3，4，5，则的个数有（ ）‎ A. 7 B. 8 C. 6 D. 5‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 集合 中一定含1,2,3,可能含4,5,6,但不同时4,5,6,由此列式可得.‎ ‎【详解】因为，2，,所以集合中一定函数元素1,2,3,‎ 又因为，2，3，4，5，,所以集合中最多含4,5,6中的2个元素,‎ 所以满足条件的集合有,,,,,,,共7个.‎ 故选.‎ ‎【点睛】本题考查了集合的子集和真子集关系,属于中档题.‎ ‎10.已知，，则与关系是（ ）‎ A. B. Ü C. Ý D. 以上都不对 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据,但,以及但可得.‎ ‎【详解】当时,,所以,令,即,解得,‎ 所以,‎ 当时,,所以,而,‎ 故选.‎ ‎【点睛】本题考查了集合之间的基本关系,属于基础题.‎ ‎11.已知是定义在R上的减函数，则实数的取值范围是（ ）‎ A. [， B. [，‎ C. D. ，]，‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 时,递减,且时的函数值恒大于或等于时的最大值.‎ ‎【详解】因为是定义在R上的减函数,‎ 所以且,‎ 解得.‎ 故选.‎ ‎【点睛】本题考查了分段函数的单调性,属于中档题.容易漏掉两段的端点值的大小关系.‎ ‎12.对于集合 ，定义=，=(M-N)(N-M)，设=，，=，则等于（ ）‎ A. ，0] B. [，0)‎ C. (，[0， D. (，][0，‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先化简集合,然后根据定义求出和,最后求并集可得.‎ ‎【详解】因为函数,所以,‎ 由函数有意义得,所以,‎ ‎,,‎ 所以.‎ 故选.‎ ‎【点睛】本题考查了集合并集运算,属于基础题.‎ 二、填空题：本题共4小题，每小题5分，共20分，请把答案填在答题卡上.‎ ‎13.设集合A={2，8，a}，B=，且BA，则a=__________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据子集的定义可得, 或,解这两个方程得解后,再检验集合中元素的互异性.‎ ‎【详解】因为集合A={2，8，a}，B=，且BA,‎ 所以或,‎ 当时,,解得或,经检验符合题意;‎ 当时,,解得,此时集合不满足元素的互异性,应舍去,‎ 综上,或.‎ 故答案为:或.‎ ‎【点睛】本题考查了子集和集合中元素的互异性,属于基础题.容易忽视集合中元素的互异性导致增解.‎ ‎14.已知二次函数的图像过点，对称轴为直线x=2,且方程=0的两个根的平方和为10，则的解析式为___________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据对称轴方程,用待定系数法设出函数解析式,然后根据以及韦达定理可解得待定系数,从而可得解析式.‎ ‎【详解】依题意设函数,‎ 由二次函数的图像过点得,‎ 所以,即,‎ 所以,‎ 令,即,‎ 所以,‎ 设方程的两根为,‎ 则,,‎ 所以,‎ 所以,解得,‎ 所以.‎ 故答案为:.‎ ‎【点睛】本题考查了用待定系数法求二次函数解析式,韦达定理,属于中档题.‎ ‎15.已知函数的定义域为R，则实数k的取值范围是___‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 构造函数,问题转化为函数图象与轴无交点,再讨论函数类型,根据二次函数的判别式列式可得.‎ ‎【详解】因为函数的定义域为R,‎ 所以对一切实数恒成立,‎ 当时,显然成立;‎ 当时,等价于二次函数的图象与轴恒不相交,‎ 所以只需判别式,解得,‎ 综上所述,.‎ 故答案为:.‎ ‎【点睛】本题考查了已知函数定义域求参数取值范围,二次函数的图象和性质,属于中档题.‎ ‎16.设是一个数集，且至少含有两个数，若对任意，都有、，、（除数），则称是一个数域.例如有理数集是数域；数集 也是数域.有下列命题：①数域必含有，两个数；②整数集是数域；③若有理数集，则数集必为数域；④数域必为无限集；⑤存在无穷多个数域.其中正确的命题的序号是_______.（把你认为正确的命题的序号填填上）‎ ‎【答案】①④⑤‎ ‎【解析】‎ 试题分析：因为，，故①正确；任意两个整数相除，商不一定都是整数，故②错误；若，则就不是数域，故③错误；因为必为任意一个数域的子集，故数域必为无限集，故④正确；例如在数域中，可将换成其它的任意一个无理数，得到的集合都是数域，所以存在无穷多个数域，故⑤正确.综上正确的有①④⑤.‎ 考点：对及时定义的概念的理解和运用.‎ 三．解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算过程.‎ ‎17.求下列函数的定义域 ‎(1)‎ ‎(2)‎ ‎【答案】（1）（2）且 ‎【解析】‎ ‎【分析】‎ ‎(1)根据二次根式被开方非负列式,解一元二次不等式可得;‎ ‎(2)根据二次根式被开方非负且零的零指数幂无意义列式,可解得.‎ ‎【详解】(1)由函数有意义,得,‎ 即,‎ 所以,‎ 解得.‎ 所以函数的定义域为.‎ ‎(2)由函数有意义,得且,‎ 解得且,‎ 故函数的定义域为且.‎ ‎【点睛】本题考查了含二次根式和零指数幂的函数的定义域的求法,属于基础题.‎ ‎18.（1）已知是一次函数，且，求；‎ ‎（2）已知，求．‎ ‎【答案】（1）或；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）设，代入已知条件可得的方程组，解方程组即可得到答案 ‎（2）利用换元法求解求出解析式 ‎【详解】（1）设，则：‎ ‎；‎ 即；‎ 解得或；‎ ‎∴或；‎ ‎（2）令，则，；‎ ‎∴；‎ ‎∴．‎ ‎【点睛】本题主要考查了求函数解析式，掌握待定系数法、换元法、配凑法、列方程组法等，由条件的不同运用适当方法解题。‎ ‎19.已知，若，则x的取值范围 ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 对和分3种情况讨论代入表达式解得结果,再求并集即可得到.‎ ‎【详解】当,即时, 可化为,‎ 即,又,所以;‎ 当,即时, 可化为,‎ 即,又,所以;‎ 当,即时,可化为,‎ 即,又,所以;‎ 综上所述: x的取值范围是.‎ ‎【点睛】本题考查了分类讨论思想,根据分段函数的自变量取值范围讨论代表达式,属于中档题.‎ ‎20.已知集合，，，，，，，且，若，则实数m的所有取值集合 ‎【答案】实数m的取值集合是{0,}‎ ‎【解析】‎ ‎【分析】‎ 先根据,得,由此列式解得或或,再验证可知,,由此可得,再根据可得.‎ ‎【详解】因为,所以,所以或,所以或或,‎ 当时,,,满足;‎ 当时,,,集合不满足元素的互异性;‎ 当时,,,此时,不符合题意,‎ 因此,.‎ 所以,‎ 由知,‎ 当时, 无解,,满足;‎ 当时,,所以,‎ 因为,所以或或或或,‎ 所以或或或或,‎ 综上所述:实数m的取值集合是{0,}.‎ ‎【点睛】本题考查了分类讨论思想,集合的交集,并集运算,子集关系,集合中元素的互异性,属于中档题.‎ ‎21.已知函数,‎ ‎（1）,，且，证明：‎ ‎（2）求函数的单调区间.‎ ‎【答案】（1）证明见解析（2）函数的增区间是，，减区间是，2]‎ ‎【解析】‎ ‎【分析】‎ ‎(1)将函数的解析式代入左边后,采取分子有理化的方式变形,化简可证.‎ ‎(2)利用单调函数的定义可以求得.‎ ‎【详解】（1）因为 ‎,‎ 所以.‎ ‎（2）函数的定义域为:,‎ 设，则,于是 ‎ ‎ ‎ ‎ 当时，，，‎ ‎∴,‎ 所以,‎ ‎∴‎ ‎∴，‎ ‎∴在，上是增函数；‎ 当时，，，‎ ‎∴,‎ 所以,‎ ‎∴‎ ‎∴，‎ ‎∴在，2]上是减函数；‎ 综上所述，函数的增区间是，，减区间是，2].‎ ‎【点睛】本题考查了恒等式证明,单调函数的定义,属于中档题.‎ ‎22.函数f(x)对任意的m，，都有，并且时，恒有 ‎(1)求证：f(x)在R上是增函数 ‎(2)若，解不等式 ‎【答案】（1）证明见解析（2）不等式的解集为:.‎ ‎【解析】‎ ‎【分析】‎ ‎(1)利用=和增函数的定义证明;‎ ‎(2)先通过赋值法得到,再根据(1)增函数可解得不等式的解集.‎ ‎【详解】(1)证明:任取,则 ‎ ‎= ‎ ‎=,‎ 因,所以,‎ 因为时，恒有,‎ 所以,所以,‎ 所以,‎ 所以,‎ 根据增函数的定义可知, f(x)在R上是增函数.‎ ‎(2)在中,令得,‎ 即,‎ 在中,令得,‎ 即,‎ 所以,‎ 又,所以 ,所以,‎ 所以等价于,‎ 因为函数在上是增函数,‎ 所以,即,‎ 所以,‎ 所以,‎ 所以不等式的解集为:.‎ ‎【点睛】本题考查了用定义证明增函数,利用增函数的性质解不等式,属于中档题.‎ ‎ ‎