【数学】2019届高考一轮复习北师大版理1-3简单的逻辑联结词、全称量词与存在量词学案

【数学】2019届高考一轮复习北师大版理1-3简单的逻辑联结词、全称量词与存在量词学案

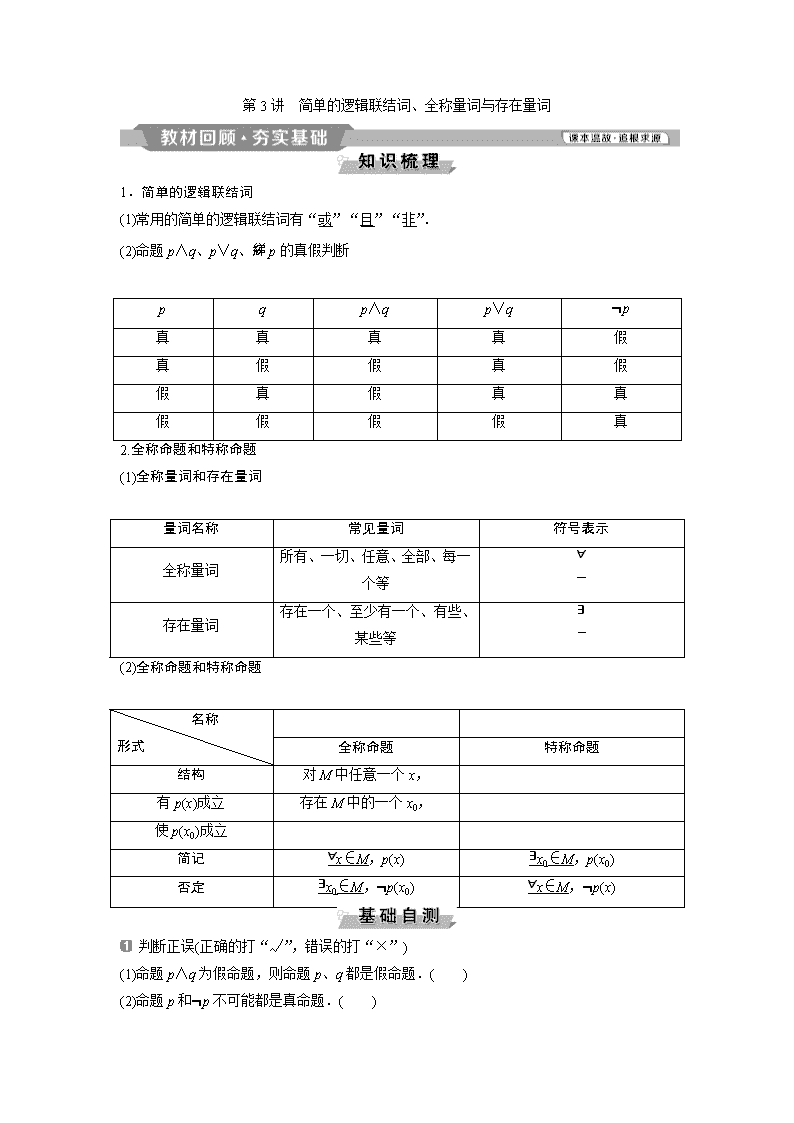
第3讲　简单的逻辑联结词、全称量词与存在量词 ‎1．简单的逻辑联结词 ‎(1)常用的简单的逻辑联结词有“或”“且”“非”．‎ ‎(2)命题p∧q、p∨q、綈p的真假判断 p q p∧q p∨q ‎¬p 真 真 真 真 假 真 假 假 真 假 假 真 假 真 真 假 假 假 假 真 ‎2.全称命题和特称命题 ‎(1)全称量词和存在量词 量词名称 常见量词 符号表示 全称量词 所有、一切、任意、全部、每一个等 ‎∀‎ 存在量词 存在一个、至少有一个、有些、某些等 ‎∃‎ ‎(2)全称命题和特称命题 ‎　　名称 形式　　‎ 全称命题 特称命题 结构 对M中任意一个x，‎ 有p(x)成立 存在M中的一个x0，‎ 使p(x0)成立 简记 ‎∀x∈M，p(x)‎ ‎∃x0∈M，p(x0)‎ 否定 ‎∃x0∈M，¬p(x0)‎ ‎∀x∈M，¬p(x)‎ ‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)命题p∧q为假命题，则命题p、q都是假命题．(　　)‎ ‎(2)命题p和¬p不可能都是真命题．(　　)‎ ‎(3)若命题p、q至少有一个是真命题，则p∨q是真命题．(　　)‎ ‎(4)写特称命题的否定时，存在量词变为全称量词．(　　)‎ ‎(5)∃x0∈M，p(x0)与∀x∈M，¬p(x)的真假性相反．(　　)‎ 答案：(1)×　(2)√　(3)√　(4)√　(5)√‎ ‎ 命题“∃x0∈R，x－x0－1>0”的否定是(　　)‎ A．∀x∈R，x2－x－1≤0‎ B．∀x∈R，x2－x－1>0‎ C．∃x0∈R，x－x0－1≤0‎ D．∃x0∈R，x－x0－1≥0‎ 解析：选A.依题意得，命题“∃x0∈R，x－x0－1>0”的否定是“∀x∈R，x2－x－1≤0”，选A.‎ ‎ 已知命题p：∃x0∈R，使sin x0＝；命题q：∀x∈R，都有x2＋x＋1>0，给出下列结论：‎ ② 命题“p∧q”是真命题；‎ ‎②命题“p∧(¬q)”是假命题；‎ ③ 命题“(¬p)∨q”是真命题；‎ ④ 命题“(¬p)∨(¬q)”是假命题．‎ 其中正确的是(　　)‎ A．②③ B．②④‎ C．③④ D．①②③‎ 解析：选A.因为>1，所以命题p是假命题．又因为x2＋x＋1＝＋≥>0，所以命题q是真命题，由命题真假的真值表可以判断②③正确，故选A.‎ ‎ (教材习题改编)命题“所有可以被5整除的整数，末位数字都是0”的否定为________________________________________________________________________．‎ 答案：“有些可以被5整除的整数，末位数字不是0”‎ ‎ 若“∀x∈，tan x≤m”是真命题，则实数m的最小值为________．‎ 解析：因为0≤x≤，所以0≤tan x≤1，‎ 又因为∀x∈，tan x≤m，故m≥1，‎ 即m的最小值为1.‎ 答案：1‎ ‎　　　　　　全称命题、特称命题(高频考点)‎ 全称命题与特称命题是高考的常考内容，多和其他数学知识相结合命题，常以选择题、填空题的形式出现．高考对全称命题、特称命题的考查主要有以下两个命题角度：‎ ‎(1)全称命题、特称命题的否定；‎ ‎(2)判断全称命题、特称命题的真假性．‎ ‎[典例引领]‎ 角度一　全称命题、特称命题的否定 ‎ 已知命题p：∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≥0，则¬p是(　　)‎ A．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0‎ B．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0‎ C．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0‎ D．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0‎ ‎【解析】　根据“全称命题q：∀x∈M，q(x)的否定是¬q：∃x0∈M，¬q(x0)”可知“¬p：∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0”．‎ ‎【答案】　C 角度二　判断全称命题、特称命题的真假性 ‎ (2018·长沙市统一模拟考试)已知函数f(x)＝x，则(　　)‎ A．∃x0∈R，f(x0)<0‎ B．∀x∈[0，＋∞)，f(x)≥0‎ C．∃x1，x2∈[0，＋∞)，<0‎ D．∀x1∈[0，＋∞)，∃x2∈[0，＋∞)，f(x1)>f(x2)‎ ‎【解析】　幂函数f(x)＝x的值域为[0，＋∞)，且在定义域上单调递增，故A错误，B正确，C错误，D选项中当x1＝0时，结论不成立，选B.‎ ‎【答案】　B ‎(1)全称命题与特称命题的否定 ‎①改写量词：找到命题所含的量词，没有量词的要结合命题的含义加上量词，再改变量词．‎ ‎②否定结论：对原命题的结论进行否定．‎ ‎(2)全、特称命题的真假判断方法 ‎①要判断一个全称命题是真命题，必须对限定集合M中的每个元素x验证p(x)‎ 成立；但要判断全称命题是假命题，只要能找出集合M中的一个x＝x0，使得p(x0)不成立即可(这就是通常所说的“举出一个反例”)．‎ ‎②要判断一个特称命题是真命题，只要在限定集合M中，至少能找到一个x＝x0，使p(x0)成立即可，否则，这一特称命题就是假命题．　 ‎ ‎ (2018·河南商丘模拟)已知f(x)＝sin x－x，命题p：∃x∈，f(x)<0，则(　　)‎ A．p是假命题，¬p：∀x∈，f(x)≥0‎ B．p是假命题，¬p：∃x∈，f(x)≥0‎ C．p是真命题，¬p：∀x∈，f(x)≥0‎ D．p是真命题，¬p：∃x∈，f(x)≥0‎ 解析：选C.易知f′(x)＝cos x－1<0，所以f(x)在上是减函数，因为f(0)＝0，所以f(x)<0，所以命题p：∃x∈，f(x)<0是真命题，綈p：∀x∈，f(x)≥0，故选C.‎ ‎　　　　　　含有逻辑联结词的命题的真假判断 ‎ [典例引领]‎ ‎ (1)(2017·高考山东卷)已知命题p：∀x>0，ln(x＋1)>0；命题q：若a＞b，则a2>b2.下列命题为真命题的是(　　)‎ A．p∧q　 B．p∧¬q C．¬p∧q D．¬p∧¬q ‎(2)已知命题p：对于任意的非零向量a，b都有a·b≤|a|·|b|；命题q：对于任意的非零实数x，都有x＋≥2.则下列命题：①p∧q，②p∨q，③p∧(¬q)，④(¬p)∨q，⑤(¬p)∧(¬q)，⑥(¬p)∨(¬q)中正确的个数为(　　)‎ A．2 B．3‎ C．4 D．5‎ ‎【解析】　(1)当x＞0时，x＋1＞1，因此ln(x＋1)＞0，即p为真命题；取a＝1，b＝－2，这时满足a＞b，显然a2＞b2不成立，因此q为假命题．易知B为真命题．‎ ‎(2)对于任意的非零向量a，b，都有a·b≤|a·b|＝|a|·|b||cos|≤|a|·|b|，即命题p为真命题，故¬p为假命题；当x<0时，x＋≤－2，即命题q为假命题，故¬q为真命题．从而p ‎∨q、p∧(¬q)、(¬p)∨(¬q)为真命题，故选B.‎ ‎【答案】　(1)B　(2)B ‎“p∨q”“p∧q”“¬p”形式命题真假的判断步骤 ‎(1)确定命题的构成形式；‎ ‎(2)判断命题p，q的真假；‎ ‎(3)根据真值表确定“p∨q”“p∧q”“ ¬p”形式命题的真假．　 ‎ ‎[通关练习]‎ ‎1．(2018·贵州省适应性考试)已知命题p：∀x∈R，log2(x2＋4)≥2，命题q：y＝x是定义域上的减函数，则下列命题中为真命题的是(　　)‎ A．p∨(¬q) B．p∧q C．(¬p)∨q D．(¬p)∧(¬q)‎ 解析：选A.命题p：函数y＝log2x在(0，＋∞)上是增函数，x2＋4≥4，所以log2(x2＋4)≥log24＝2，即命题p是真命题，因此¬p为假命题；命题q：y＝x在定义域上是增函数，故命题q是假命题，¬q是真命题．因此选项A是真命题，选项B是假命题，选项C是假命题，选项D是假命题，故选A.‎ ‎2．(2018·南昌市第一次模拟测试)已知命题p：函数f(x)＝|cos x|的最小正周期为2π；命题q：函数y＝x3＋sin x的图象关于原点中心对称，则下列命题是真命题的是(　　)‎ A．p∧q B．p∨q C．(¬p)∧(¬q) D．p∨(¬q)‎ 解析：选B.因为命题p为假，命题q为真，所以p∨q为真命题．‎ ‎　　　　　　由命题的真假确定参数的取值范围 ‎ [典例引领]‎ ‎ (1)已知f(x)＝ln(x2＋1)，g(x)＝()x－m，若对∀x1∈[0，3]，∃x2∈[1，2]，使得f(x1)≥g(x2)，则实数m的取值范围是(　　)‎ A．[，＋∞) B．[，＋∞)‎ C．(－∞，] D．(－∞，－]‎ ‎(2)(分类讨论思想)给定命题p：对任意实数x都有ax2＋ax＋1>0成立；q：关于x的方程x2－‎ x＋a＝0有实数根．如果p∨q为真命题，p∧q为假命题，则实数a的取值范围为________．‎ ‎【解析】　(1)当x∈[0，3]时，f(x)min＝f(0)＝0，‎ 当x∈[1，2]时，‎ g(x)min＝g(2)＝－m，‎ 由f(x)min≥g(x)min，‎ 得0≥－m，所以m≥，故选A.‎ ‎(2)当p为真命题时，“对任意实数x都有ax2＋ax＋1>0成立”⇔a＝0或 所以0≤a<4.‎ 当q为真命题时，“关于x的方程x2－x＋a＝0有实数根”⇔Δ＝1－4a≥0，所以a≤.‎ 因为p∨q为真命题，p∧q为假命题，‎ 所以p，q一真一假．‎ 所以若p真q假，则0≤a<4，且a>，‎ 所以4.‎ ‎2．已知命题p：“∀x∈[0，1]，a≥ex”，命题q：“∃x0∈R，x＋4x0＋a＝0”，若命题“p∧q”是真命题，则实数a的取值范围是(　　)‎ A．(4，＋∞) B．[1，4]‎ C．[e，4] D．(－∞，－1)‎ 解析：选C.由题意知p与q均为真命题，由p为真，可知a≥e，由q为真，知x2＋4x＋a＝0有解，则Δ＝16－4a≥0，所以a≤4.综上可知e≤a≤4.‎ ‎ 含逻辑联结词命题真假的等价关系 ‎(1)p∨q真⇔p，q至少一个真⇔(¬p)∧(¬q)假．‎ ‎(2)p∨q假⇔p，q均假⇔(¬p)∧(¬q)真．‎ ‎(3)p∧q真⇔p，q均真⇔(¬p)∨(¬q)假．‎ ‎(4)p∧q假⇔p，q至少一个假⇔(¬p)∨(¬q)真．‎ ‎(5)¬p真⇔p假；¬p假⇔p真．‎ ‎ 全称命题与特称命题真假的判断方法 命题名称 真假 判断方法一 判断方法二 全称命题 真 所有对象使命题真 否定为假 假 存在一个对象使命题假 否定为真 特称命题 真 存在一个对象使命题真 否定为假 假 所有对象使命题假 否定为真 ‎ 根据命题的真假求参数的取值范围的方法步骤 ‎(1)求出当命题p，q为真命题时所含参数的取值范围；‎ ‎(2)根据复合命题的真假判断命题p，q的真假性；‎ ‎(3)根据命题p，q的真假情况，利用集合的交集和补集的运算，求解参数的取值范围．‎ ‎ 易错防范 ‎(1)注意命题是全称命题还是特称命题，是正确写出命题的否定的前提；‎ ‎(2)注意命题所含的量词，对于量词隐含的命题要结合命题的含义显现量词，再进行否定；‎ ‎(3)复合命题的否定 ‎①“¬p”的否定是“p”；②“p∨q”的否定是“¬p∧¬q”；③“p∧q”的否定是“¬p∨¬q”．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ‎ ‎1．设两个命题p：对所有整数x，x2－1＝0，q：对所有整数x，5x－1是整数．则(　　)‎ A．p是真命题，q是真命题 B．p是真命题，q是假命题 C．p是假命题，q是真命题 D．p是假命题，q是假命题 解析：选C.因为当x＝0时，x2－1＝－1≠0，所以p是假命题；因为q是真命题，所以选C.‎ ‎2．(2018·合肥市第二次教学质量检测)已知命题q：∀x∈R，x2>0，则(　　)‎ A．命题¬q：∀x∈R，x2≤0为假命题 B．命题¬q：∀x∈R，x2≤0为真命题 C．命题¬q：∃x∈R，x2≤0为假命题 D．命题¬q：∃x∈R，x2≤0为真命题 解析：选D.全称命题的否定是将“任意”改为“存在”，然后再否定结论．又当x＝0时，x2≤0成立，所以綈q为真命题，故选D.‎ ‎3．(2018·湖北武汉调研)命题“y＝f(x)(x∈M)是奇函数”的否定是(　　)‎ A．∃x∈M，f(－x)＝－f(x)‎ B．∀x∈M，f(－x)≠－f(x)‎ C．∀x∈M，f(－x)＝－f(x)‎ D．∃x∈M，f(－x)≠－f(x)‎ 解析：选D.命题“y＝f(x)(x∈M)是奇函数”的否定是∃x∈M，f(－x)≠－f(x)，故选D.‎ ‎4．以下四个命题既是特称命题又是真命题的是(　　)‎ A．锐角三角形有一个内角是钝角 B．至少有一个实数x，使x2≤0‎ C．两个无理数的和必是无理数 D．存在一个负数x，>2‎ 解析：选B.A中锐角三角形的内角都是锐角，所以A是假命题；B中当x＝0时，x2＝0，满足x2≤0，所以B既是特称命题又是真命题；C中因为＋(－)＝0不是无理数，所以C是假命题；D中对于任意一个负数x，都有<0，不满足>2，所以D是假命题．‎ ‎5．(2018·南昌模拟)已知命题p：“∀x∈R，x＋1≥0”的否定是“∀x∈R，x＋1<0”；命题q：函数y＝x－3是幂函数．则下列命题为真命题的是(　　)‎ A．p∧q　 B．p∨q C．¬q D．p∧(¬q)‎ 解析：选B.易知命题p是假命题，命题q是真命题，所以p∨q是真命题．‎ ‎6．命题p：甲的数学成绩不低于100分，命题q：乙的数学成绩低于100分，则p∨(綈q)表示(　　)‎ A．甲、乙两人的数学成绩都低于100分 B．甲、乙两人至少有一人的数学成绩低于100分 C．甲、乙两人的数学成绩都不低于100分 D．甲、乙两人至少有一人的数学成绩不低于100分 解析：选D.由于命题q：乙的数学成绩低于100分，因此¬q：乙的数学成绩不低于100分．所以p∨(¬q)：甲、乙两人至少有一人的数学成绩不低于100分，故选D.‎ ‎7．已知命题p：函数y＝ax(a>0且a≠1)在R上是增函数，命题q：loga2＋log2a≥2(a>0且a≠1)，则下列命题为真命题的是(　　)‎ A．p∨q B．p∧q C．(¬p)∧q D．p∨(¬q)‎ 解析：选D.当0m”是真命题，则m的值可以是(　　)‎ A．－ B．1‎ C. D. 解析：选A.因为sin xcos x＝sin 2x∈，所以m<.故选A.‎ ‎9．已知命题p：∀x∈R，2x<3x，命题q：∃x∈R，x2＝2－x，若命题(¬p)∧q为真命题，则x的值为(　　)‎ A．1 B．－1‎ C．2 D．－2‎ 解析：选D.因为¬p：∃x∈R，2x≥3x，要使(¬p)∧q为真，所以¬p与q同时为真．由2x≥3x得≥1，所以x≤0，由x2＝2－x得x2＋x－2＝0，所以x＝1或x＝－2，又x≤0，所以x＝－2.‎ ‎10．已知命题p：∃x∈R，x2＋1<2x；命题q：若mx2－mx＋1>0恒成立，则00恒成立，则m＝0或则0≤m<4，所以命题q为假，故选C.‎ ‎11．(2018·江西红色七校联考)已知函数f(x)＝给出下列两个命题：命题p：∃m∈(－∞，0)，方程f(x)＝0有解，命题q：若m＝，则f(f(－1))＝0，那么，下列命题为真命题的是(　　)‎ A．p∧q B．(¬p)∧q C．p∧(¬q) D．(¬p)∧(¬q)‎ 解析：选B.因为3x>0，当m<0时，m－x2<0，所以命题p为假命题；当m＝时，因为f(－1)＝3－1＝，‎ 所以f(f(－1))＝f＝－＝0，‎ 所以命题q为真命题，‎ 逐项检验可知，只有(¬p)∧q为真命题，故选B.‎ ‎12．(2018·郑州市第二次质量预测卷)下列命题是真命题的是(　　)‎ A．∀φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数 B．∃α，β∈R，使cos(α＋β)＝cos α＋cos β C．向量a＝(2，1)，b＝(－1，0)则a在b的方向上的投影为2‎ D．“|x|≤1”是“x≤1”的既不充分也不必要条件 解析：选B.选项A，当φ＝时，f(x)＝cos 2x，其为偶函数，故A为假命题；选项B，令α＝，β＝－，则cos(α＋β)＝cos(－)＝，cos α＋cos β＝＋0＝，cos(α＋β)＝cos α＋cos β成立，故B为真命题；选项C，设a与b的夹角为θ，则a在b的方向上的投影为＝＝－2，故C为假命题；选项D，|x|≤1，－1≤x≤1，故充分性成立，若x≤1，|x|≤1不一定成立，‎ 故为充分不必要条件，D为假命题．‎ ‎13．命题p的否定是“对所有正数x，>x＋1”，则命题p可写为____________________．‎ 解析：因为p是¬p的否定，所以只需将全称命题变为特称命题，再对结论否定即可．‎ 答案：∃x0∈(0，＋∞)，≤x0＋1‎ ‎14．已知命题p：x2＋4x＋3≥0，q：x∈Z，且“p∧q”与“¬q”同时为假命题，则x＝________．‎ 解析：若p为真，则x≥－1或x≤－3，‎ 因为“¬q”为假，则q为真，即x∈Z，‎ 又因为“p∧q”为假，所以p为假，故－30”是真命题，故Δ＝22－4m<0，即m>1，故a＝1.‎ 答案：1‎ ‎16．已知下列命题．‎ ‎①∃x0∈，sin x0＋cos x0≥；‎ ‎②∀x∈(3，＋∞)，x2>2x＋1；‎ ‎③∀x∈R，2x＋>2；‎ ‎④∃x∈，tan x>sin x.‎ 其中真命题为________．(填所有真命题的序号)‎ 解析：对于①，当x＝时，sin x＋cos x＝，‎ 所以此命题为真命题；‎ 对于②，当x∈(3，＋∞)时，‎ x2－2x－1＝(x－1)2－2>0，‎ 所以此命题为真命题；‎ 因为2x>0，所以＋2x≥2＝2，‎ 当且仅当＝2x即x＝0时等号成立．‎ 所以此命题为假命题；‎ 对于④，当x∈时，tan x<00的解集为R，则实数a∈(0，4)，命题q：“x2－2x－8>0”是“x>5”的必要不充分条件，则下列命题正确的是(　　)‎ A．p∧q B．p∧(¬q)‎ C．(¬p)∧(¬q) D．(¬p)∧q 解析：选D.命题p：a＝0时，可得1>0恒成立；a≠0时，可得解得00解得x>4或x<－2.因此“x2－2x－8>0”是“x>5”的必要不充分条件，是真命题．故(¬p)∧q是真命题．故选D.‎ ‎2．(2018·湖北黄冈模拟)下列四个命题：‎ ‎①若x>0，则x>sin x恒成立；‎ ‎②命题“若x－sin x＝0，则x＝0”的逆否命题为“若x≠0，则x－sin x≠0”；‎ ‎③“命题p∧q为真”是“命题p∨q为真”的充分不必要条件；‎ ‎④命题“∀x∈R，x－ln x>0”的否定是“∃x0∈R，x0－ln x0<0”．‎ 其中正确命题的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选C.对于①，令y＝x－sin x，则y′＝1－cos x≥0，则函数y＝x－sin x在R上递增，则当x>0时，x－sin x>0－0＝0，即当x>0时，x>sin x恒成立，故①正确；‎ 对于②，命题“若x－sin x＝0，则x＝0”的逆否命题为“若x≠0，则x－sin x≠0”，故②正确；‎ 对于③，命题p∨q为真即p，q中至少有一个为真，p∧q为真即p，q都为真，可知“p∧q为真”是“p∨q为真”的充分不必要条件，故③正确；‎ 对于④，命题“∀x∈R，x－ln x>0”的否定是“∃x0∈R，x0－ln x0≤0”，故④错误．‎ 综上，正确命题的个数为3，故选C.‎ ‎3．已知命题p：∃x0∈R，x0－2>lg x0；命题q：∀x∈R，－x2＋x－1<0.给出下列结论：‎ ‎①命题“p∧q”是真命题；‎ ‎②命题“p∧(¬q)”是假命题；‎ ‎③命题“(¬p)∨q”是真命题；‎ ‎④命题“p∨(¬q)”是假命题．‎ 其中所有正确结论的序号为________．‎ 解析：对于命题p，取x＝10，则有10－2>lg 10成立，故命题p为真命题；对于命题q，方程－x2＋x－1＝0，即x2－x＋1＝0，Δ＝1－4×1<0，故方程无解，所以命题q为真命题．综上“p∧q”是真命题，“p∧(¬q)”是假命题，“(¬p)∨q”是真命题，“p∨(¬q)”是真命题，即正确的结论为①②③.‎ 答案：①②③‎ ‎4．下列说法：‎ ‎①若命题p：∃x0∈R，tan x0＝2；命题q：∀x∈R，x2－x＋>0.则命题“p∧(¬q)”是假命题；‎ ‎②已知直线l1：ax＋3y－1＝0，l2：x＋by＋1＝0，则l1⊥l2的充要条件是＝－3；‎ ‎③“设a，b∈R，若ab≥2，则a2＋b2>4”的否命题为：“设a，b∈R，若ab<2，则a2＋b2≤4”．‎ 其中正确说法的序号为________．(把你认为正确说法的序号都填上)‎ 解析：在①中，命题p是真命题，命题q也是真命题，故“p∧(綈q)”是假命题是正确的．在②中，由l1⊥l2，得a＋3b＝0，所以②不正确．在③中“设a，b∈R，若ab≥2，则a2＋b2>4”的否命题为：“设a，b∈R，若ab<2，则a2＋b2≤4”正确．‎ 答案：①③‎ ‎5．已知命题p：“存在a>0，使函数f(x)＝ax2－4x在(－∞，2]上单调递减”，命题q：“存在a∈R，使∀x∈R，16x2－16(a－1)x＋1≠0”．若命题“p∧q”为真命题，求实数a的取值范围．‎ 解：若p为真，则对称轴x＝－＝在区间(－∞，2]的右侧，则≥2，所以00，若r是綈t的必要不充分条件，求正数m的值．‎ 解：(1)若p为真，则3a≤9，得a≤2.‎ 若q为真，则函数f(x)无极值点，所以f′(x)＝x2＋3(3－a)x＋9≥0恒成立，‎ 得Δ＝9(3－a)2－4×9≤0，解得1≤a≤5.‎ 因为“p∧q”为假命题，“p∨q”为真命题，‎ 所以p与q只有一个命题是真命题．‎ 若p为真命题，q为假命题，则⇒a<1；‎ 若q为真命题，p为假命题，则⇒20，‎ 所以(a－m)>0，所以am＋，‎ 即t：am＋，从而綈t：m≤a≤m＋，‎ 因为r是¬t的必要不充分条件，所以¬t⇒r，r⇒/¬t，‎ 所以(两个不等式不能同时取等号)，‎ 解得1≤m≤，又因为m∈N*，所以m＝1.‎