- 2021-06-11 发布 |
- 37.5 KB |
- 8页

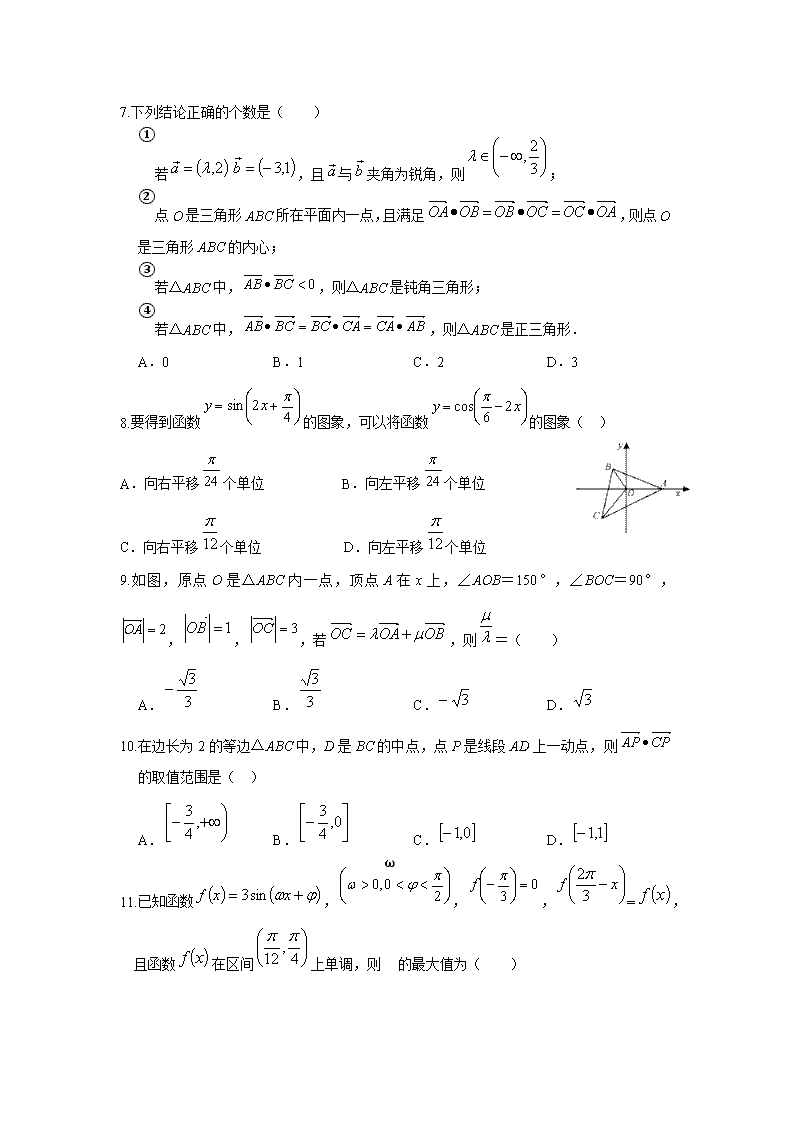

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年河南省周口扶沟县高级中学高一下学期第二次月考数学试题
2018-2019学年河南省周口扶沟县高级中学高一下学期第二次月考数学试题 一、选择题:(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。) 1.已知,则角的终边位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.与﹣2002°终边相同的最小正角是( ) A.158° B.100° C.78° D.22° 3..若,则等于( ) A. B. C. D. 4.已知则=( ) A. B. C. D. 5.已知平面上三点不共线,O是不同于A,B,C的任意一点,若,则△ABC是( ) A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形 6.下列函数中,以2π为周期,为对称轴,且在上单调递增的函数是( ) A. B. C. D. 7.下列结论正确的个数是( ) ①若,且与夹角为锐角,则; ②点O是三角形ABC所在平面内一点,且满足,则点O是三角形ABC的内心; ③若△ABC中,,则△ABC是钝角三角形; ④若△ABC中,,则△ABC是正三角形. A.0 B.1 C.2 D.3 8.要得到函数的图象,可以将函数的图象( ) A.向右平移个单位 B.向左平移个单位 C.向右平移个单位 D.向左平移个单位 9.如图,原点O是△ABC内一点,顶点A在x上,∠AOB=150°,∠BOC=90°,,,,若,则=( ) A. B. C. D. 10.在边长为2的等边△ABC中,D是BC的中点,点P是线段AD上一动点,则的取值范围是( ) A. B. C. D. 11.已知函数,,,=,且函数在区间上单调,则ω的最大值为( ) A. B. C. D. 12.已知,,则的取值范围是( ) A. B. C. D. 二、填空题(每小题5分,共20分) 13.已知角终边上的一点,则的值为___________. 14.已知,则与方向相同的单位向量是___________. 15.=____________. 16.将函数的图象向右平移个单位得到函数的图象,则以函数与的图象的相邻三个交点为顶点的三角形的面积为___________. 三、解答题:(本大题共6小题,共70分,解答应写出文字说明及演算步骤.。) 17.(本小题满分10分)已知向量的夹角为,且. (1)在指定的位置用尺规作出向量; (2)求与的夹角的余弦值; (3)求(λ∈R)的最小值. 18.(本小题满分12分)已知,. (1)求的值; (2)求的值. 19.(本小题满分12分)在平面直角坐标系中,O为坐标原点. (1)A、B、C三点满足,求证:A、B、C三点共线; (2)已知,函数,求使不等式成立的的取值范围. 20.(本小题满分12分)已知函数(M>0,ω>0,)的部分图象如图所示,其中P,Q分别为函数f(x)图象相邻的一个最高点和最低点,P,Q两点的横坐标分别为1和4,且. (1)求函数f(x)的最小正周期和单调递增区间; (2)当时,求函数的值域. 21.(本小题满分12分)已知函数 (1)设,将函数f(x)表示为关于的函数,求的解析式; (2)对任意,不等式恒成立,求的取值范围. 22(本小题满分12分).已知实数0≤θ≤π,,,若向量满足,且. (Ⅰ)若,求 (Ⅱ)若在上为增函数. (1)求实数的取值范围; (2)若对满足题意的恒成立,求的取值范围. 2018-2019学年度高一下期第二次质量检测 数学试题答案 一. 选择题: CAADA CBADB CC 一. 填空题: 13. 14: 15: 16: 二. 解答题: 17题:解:(1)已知向量,作有向线段,连接BA, 则向量; ,同理,所以与夹角的余弦值为; (3)因为,当λ=1时取得最小值为3,所以的最小值是. 18题:解:因为,, 所以 因为,所以,又,所以 19题:解:(1)证明:由,得,得, ∴,为共线向量,∴A,B,C三点共线; (2)f(x)==(sinx,cosx)•(sinx+cosx,2cosx) =sin2x+sinxcosx+2cos2x==, 由f(x),得sin(2x+)≥0,∴2kπ≤2x+≤2kπ+π,k∈Z, ∴,k∈Z,故x的取值范围为,k∈Z 20题:解:(1)由图可知,所以, 又因为P(1,M),Q(4,﹣M),所以OP•OQ==0⇒M=2, 又因为(k∈Z), 因为,所以.所以函数, 令,k∈Z, 解得6k﹣2≤x≤6k+1,k∈Z,所以函数f(x)的单调递增区间为[6k﹣2,6k+1](k∈Z) 因为, 所以= 又因为,所以.所以. 21题:解:(1) t2=sin2x+cos2x+2sinxcosx,sinxcosx=. f(x)=1﹣cos(2x+)﹣2(cosx+sinx)﹣5a+2 =3+sin2x﹣2(sinx+cosx)﹣5a =3+2sinxcosx﹣2(sinx+cosx)﹣5a =3+2×﹣2t﹣5a=t2﹣2t﹣5a+2, f(x)=g(t)=t2﹣2t﹣5a+2([﹣,]); (2)x∈[0,], t=sinx+cosx=sin(x+),t∈[1,], 又g(t)=t2﹣2t﹣5a+2=(t﹣1)2﹣5a+1在区间[1,]上单调递增, 所以g(t)min=g(1)=1﹣5a,从而f(x)min=1﹣5a, 要使不等式f(x)6﹣2a在区间[0,]上恒成立, 只要1﹣5a6﹣2a,解得a. 22题:解:(Ⅰ)设=(x0,y0),则(x0+cosθ,y0+sinθ),, 由=2得 ()2=4,得﹣2+=4,得1﹣0+2=4, 得=,,y0+sinθ=0,y0=﹣sinθ, ,x0cosθ+y0sinθ=0,x0=, ∴2=x02+y02=3⇒()2+(﹣sinθ)2=3⇒或或或, 或或或, 或或或 (Ⅱ)(1)== 在[,+∞)上为增函数,所以对称轴,即, 设=(x0,y0),则, 又,且,y0=﹣sinθ,x0=, =x02+y02=()2+sin2θ≤1,即 sin2θ≤cos2θ,cos2θ, cosθ∈[,1]∪[﹣1,﹣], θ∈[0,][,], (2)由(1)知(1+)x2﹣2x+15,即(x2﹣2x)+x2﹣40对任意01恒成立, ,解得:查看更多