- 2021-06-10 发布 |
- 37.5 KB |
- 10页

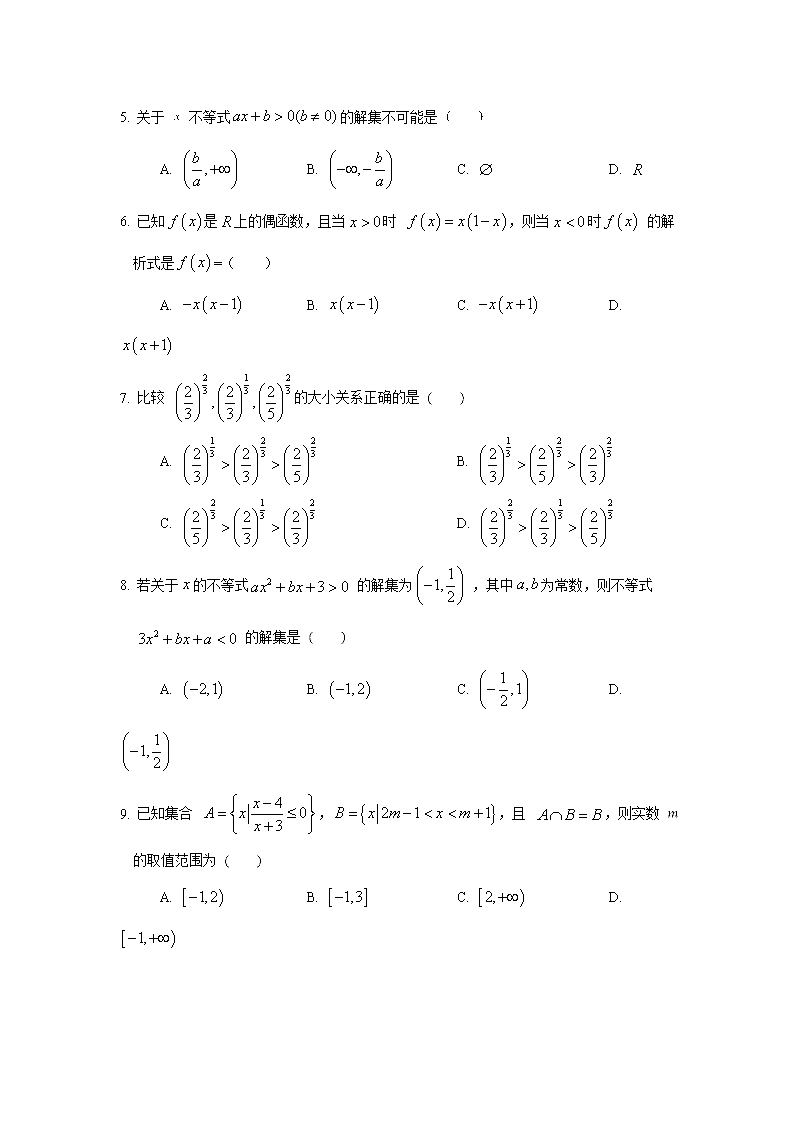

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年四川省成都石室中学高一10月月考数学试题
2018-2019学年四川省成都石室中学高一10月月考数学试题 说明:考试时间120分钟,总分150分 一、选择题(共12小题;共60分) 1. 集合,集合,则 A. B. C. D. 2. 下列各组函数中,表示同一函数的是 A. 与 B. 与 C. 与 D.与 3. 函数 的单调递增区间是 A. B. C. D. 4. 某工厂 年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量保持不变,则该厂 年来这种产品的总产量 与时间 (年)的函数关系图象最有可能是 A. B. C. D. 5. 关于 不等式的解集不可能是 A. B. C. D. 6. 已知是上的偶函数,且当时 ,则当时 的解析式是=( ) A. B. C. D. 7. 比较 的大小关系正确的是 A. B. C. D. 8. 若关于的不等式 的解集为 ,其中为常数,则不等式 的解集是 A. B. C. D. 9. 已知集合 ,,且 ,则实数 的取值范围为 A. B. C. D. 10. 函数 值域为,则实数的取值范围是 A. B. C. D. 11. 已知,则不等式 的解集为 A. B. C. D. 12. 设函数 与 的定义域为 ,且 单调递增,,.若对任意 ,不等式 恒成立.则 A. 都是增函数 B. 都是减函数 C. 是增函数, 是减函数 D. 是减函数, 是增函数 二、填空题(共4小题;共20分) 13.若函数 是奇函数,则实数 的值为 . 14. 已知函数的定义域是 ,则函数 的定义域是 . 15.若直线y=a与函数 (a>0且a≠1)的图象有两个公共点,则a的取值范围是________________. 16. 已知定义在上的函数,满足,函数的图象关于点中心对称,且对任意的负数, 恒成立,则不等式的解集为____________. 三、解答题(共6小题;共70分) 17.已知集合,,. (1)求; (2)若且,求实数的取值范围. 18.(1)计算:; (2)求二次函数 在区间的最大值. 19.某工厂生产甲、乙两种产品所得利润分别为和(万元),它们与投入资金(万元)的关系有如下公式:,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元. (1)设对乙种产品投入资金(万元),求总利润(万元)关于的函数关系式及其定义域; (2)如何分配投入资金,才能使总利润最大,并求出最大总利润. 20. 设函数. (1)讨论函数的奇偶性,并说明理由. (2)若,试判断函数在区间上的单调性,并用函数单调性定义给出证明. 21.设函数 ,其中 . (1)当 时,求不等式 的解集; (2)若不等式 在恒成立,求实数的取值范围. 22. 定义域为的函数 满足:对于任意的实数都有成立,且当 时, 恒成立,且 .(是一个给定的正整数). (1)判断函数 的奇偶性,并证明你的结论; (2)证明 为减函数;若函数在 上总有 成立,试确定 应满足的条件; (3)当时,解关于 的不等式 . 成都石室中学2018—2019学年度上期高2021届10月月考 数学参考答案 一、 选择题 1-5:BDCAA 6-10:CABDD 11、12:CA 二、 填空题: 13: 14: 15: 16: 三、 解答题: 17:解:(1) ………………………2′ ………………………3′ ………………………5′ (2)由A∩C≠A,则 ………………………7′ 由C∩B≠∅,则 ………………………9′ 综上: ………………………10′ 18: (1)解: 原式==; ………………………6′ (2)解: 对称轴 ………………………7′ 当,即时,……………………9′ 当,即时,……………………11′ 综上: ………………………12′ 19. 解:(1) ………………………3′ 由,解得,即定义域为……………………5′ (2)令,,则……………………7′ ,……………………8′ 所以当即时, …………………… 10′ 答:当甲种产品投入资金164万元,乙种产品投入资金36万元时,总利润最大. 最大总利润是248万元. …………………… 12′ 20:解:(Ⅰ) --------- 1分 当时,, ,为奇函数;--------- 3分 当时,, , 不是偶函数;--------- 4分 , 不是奇函数;--------- 5分 故当时,是非奇非偶函数. ---------6分 (2)任取,, ---------7分 ---------9分 ,,且,,. 于是,从而,即---------11分 所以函数在区间上单调递增. ---------12分 21:解:(1) 当 时,不等式 ,即 ,即 , ------1分 或 ------5分 故不等式 的解集为 . ------6分 (2) 由题意可得: 在x 恒成立 (用公式法或函数法对应给分) ------12分 22:解:(1) 为奇函数,证明如下; 由已知对于任意 ,, ------1分 恒成立. 令 ,得 , 所以 . ------2分 令 ,得 . 所以对于任意 ,都有 . 所以 是奇函数. ------4分 (2) 设任意 且 ,则 ,由已知 , 又 , 由 得 , 根据函数单调性的定义知 在 上是减函数. ------6分 所以 在 上的最大值为 . 要使 恒成立,当且仅当 , 又因为 所以 . 又 ,, 所以 . ------8分 (3) , 所以 . 所以 , 所以 , 因为 在 上是减函数, 所以 .即 , ------10分 因为 ,所以 . 讨论: ① 当 ,即 时,原不等式的解集为 ; ② 当 ,即 时,原不等式的解集为 ; ③ 当 ,即 时,原不等式的解集为 .---12分 查看更多