- 2021-06-10 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020学年高二数学上学期第一次月考试题 文(普通班) 新人教版
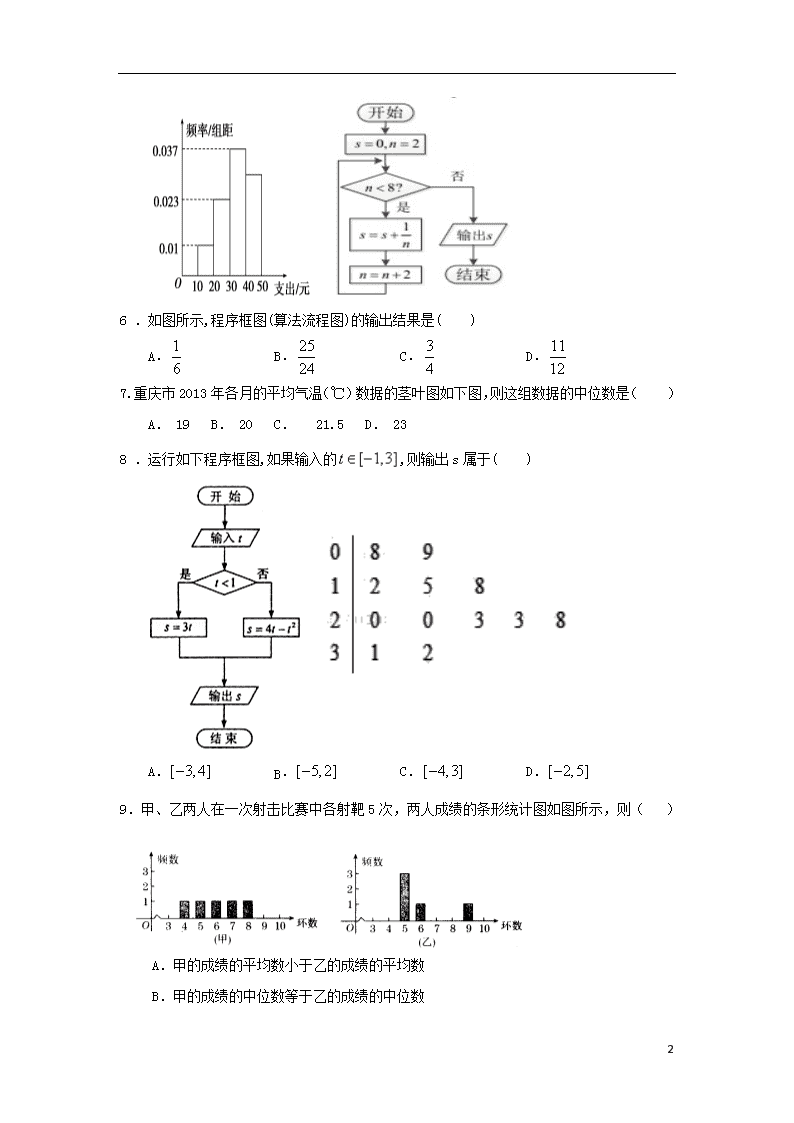
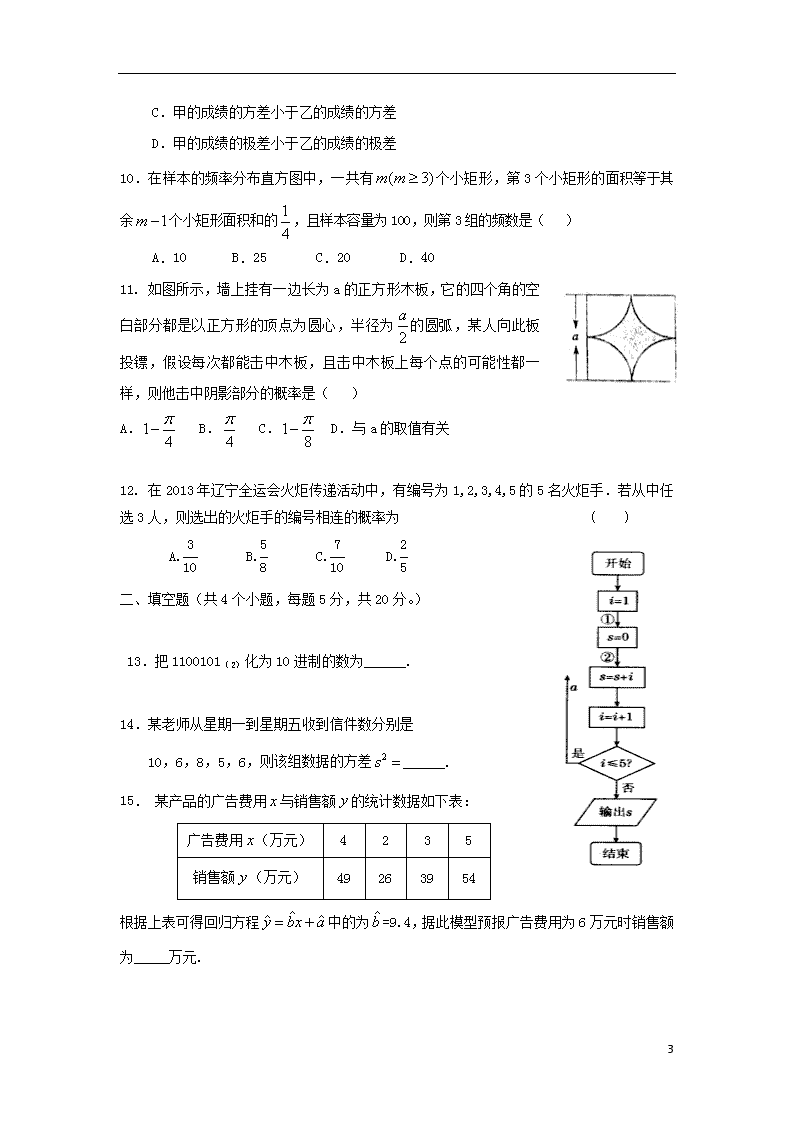
2019学年第一学期第一次月考 数学试题(高二文) 考试时间 120分钟 试题分数 150分 一、 选择题:(每题只有一个正确选项。共12个小题,每题5分,共60分。) 3. 一班有学员54人,二班有学员42人,现在要用分层抽样的方法从两个班中抽出一部分人参加4×4方队进行军训表演,则一班和二班分别被抽取的人数是( ) A.9人、7人 B.15人、1人 C.8人、8人 D.12人、4人 4.李明所在的高二(5)班有51名学生,学校要从该班抽出5人开座谈会,若采用系统抽样法,需先剔除一人,再将留下的50人平均分成5个组,每组各抽一人,则李明参加座谈会的机会为( ) (A) (B) (C) (D) 5.学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( ) A.100 B.120 C.130 D.390 10 6 .如图所示,程序框图(算法流程图)的输出结果是( ) A. B. C. D. 7.重庆市2013年各月的平均气温(℃)数据的茎叶图如下图,则这组数据的中位数是( ) A. 19 B. 20 C. 21.5 D. 23 8 .运行如下程序框图,如果输入的,则输出s属于( ) A. B. C. D. 9.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( ) A.甲的成绩的平均数小于乙的成绩的平均数 B.甲的成绩的中位数等于乙的成绩的中位数 10 C.甲的成绩的方差小于乙的成绩的方差 D.甲的成绩的极差小于乙的成绩的极差 10.在样本的频率分布直方图中,一共有个小矩形,第3个小矩形的面积等于其余个小矩形面积和的,且样本容量为100,则第3组的频数是( ) A.10 B.25 C.20 D.40 11. 如图所示,墙上挂有一边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( ) A. B. C. D.与a的取值有关 12. 在2013年辽宁全运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手.若从中任选3人,则选出的火炬手的编号相连的概率为 ( ) A. B. C. D. 二、 填空题(共4个小题,每题5分,共20分。) 13.把1100101(2)化为10进制的数为______. 14. 某老师从星期一到星期五收到信件数分别是 10,6,8,5,6,则该组数据的方差______. 15. 某产品的广告费用与销售额的统计数据如下表: 广告费用(万元) 4 2 3 5 销售额(万元) 49 26 39 54 根据上表可得回归方程中的为=9.4,据此模型预报广告费用为6万元时销售额为_____万元. 16. 如图所示的程序框图(未完成),设当箭头指向①时,输出的结果,当箭头指向② 10 时,输出的结果,则_____. 三、 解答题:(解答题应写出必要的文字说明和演算步骤) 17.(本小题满分10分)黄种人群中各种血型的人所占的比例如下: 血型 A B AB O 该血型的人所占比例(%) 28 29 8 35 已知同种血型的人可以输血,O型血可以输给任何一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问: (1)任找一个人,其血可以输给小明的概率是多少? (2)任找一个人,其血不能输给小明的概率是多少? 18.(本小题满分12分)某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:,,,,. (Ⅰ)求图中a的值; (Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分和中位数(要求写出计算过程,结果保留一位小数). 19.(本小题满分12分) 某车间共有 10 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. (Ⅰ) 根据茎叶图计算样本均值; (Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间名工人中有几名优秀工人; (Ⅲ) 从该车间名工人中,任取2人,求恰有1名优秀工人的概率. 20. (本小题满分12分) 有两个不透明的箱子,每个箱子里都装有4个完全相同的小球,球上分别标有数字1, 2, 3, 4. (I )甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出一个球,谁摸出的球上标的数字大谁获胜(若数字相同则为平局),求甲获胜的概率; (II)摸球方法与(1)相同,若规定:两人摸到的球上所标数字相同甲获胜,所标数 字不同则乙获胜,这样规定公平吗?请说明理由. 21. (本小题满分12分) 设事件表示“关于的方程有实数根”. (1)若、,求事件发生的概率; (2)若、,求事件发生的概率. 22. (本题满分12分) 10 如表,其提供了某厂节能降耗技术改造生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据. (1)请画出表中数据的散点图; (2)请根据表中提供的数据,用最小二乘法求出y关于x的回归方程 (参考:用最小二乘法求线性回归方程系数公式 ,) 数学答案 (高二文科) 选择题 DBACA DBACC AA 10 13. 101 14. 15. 65.5 16. 20 17. (本小题满分10分) 解 (1)对任一人,其血型为A、B、AB、O型血的事件分别记为 A′、B′、C′、D′,它们是互斥的.由已知,有 P(A′)=0.28,P(B′)=0.29, P(C′)=0.08,P(D′)=0.35. 因为B、O型血可以输给B型血的人, 故“可以输给B型血的人”为事件B′∪D′. 根据互斥事件的加法公式,有 P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64. (2) 由于A、AB型血不能输给B型血的人, 故“不能输给B型血的人”为事件A′∪C′, 且P(A′∪C′)=P(A′)+P(C′)=0.28+0.08=0.36. 18. (本小题满分12分) 解: (1) 依题意得,, 解得。 (2) 这100名学生语文成绩的平均分为: (分) 中位数为:70+10(分). 19. (本小题满分12分)解:(1)由题意可知, 样本均值 (2)样本6名个人中日加工零件个数大于样本均值的工人共有2名, 10 可以推断该车间12名工人中优秀工人的人数为: (3)从该车间12名工人中,任取2人有种方法, 而恰有1名优秀工人有 所求的概率为: 19. 解:(1)用(表示甲摸到的数字,表示乙摸到的数字) 表示甲乙各摸到一球构成的基本事件有: (1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4) (3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4) 共有16个 ---------------3分 设甲获胜的事件为, 则事件包括的基本事件为(2,1)(3,1)(3,2) (4,1)(4,2)(4,3)共有6个, --------5分 ,即甲获胜的概率为 ----------6分 (2) 设甲获胜的事件为,乙获胜的事件为, 事件所包含的基本事件为(1,1)(2,2)(3,3)(4,4) 共有4个, -------------8分 则,, -----------10分 ,∴ 不公平 -----------12分 21. (本小题满分12分) 10 解:(1)由关于的方程有实数根,得. ∴,故, 当,时,得.…… 2分 若、,则总的基本事件数(即有序实数对的个数) 为. 事件包含的基本事件为:,,, ,,,共有个. ∴事件发生的概率; ………… 7分 (2)若、,则总的基本事件所构成的区域 , 是平面直角坐标系中的一个正方形(如右图的四边形), 其面积. ………… 9分 事件构成的区域是 , 是平面直角坐标系中的一个 等腰直角三角形(如右图的阴影部分), 其面积. 故事件发生的概率. …… 12分 22、(本小题满分12分)思路解析:作散点图求出求得回归方程 10 解答:(1)题设所给数据,可得散点图如图. (2)对照数据,计算得: , 所以,由最小二乘法确定的回归方程的系数为: 因此,所求的线性回归方程为. 10查看更多