- 2021-06-10 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第二章(第22课时)对数函数3
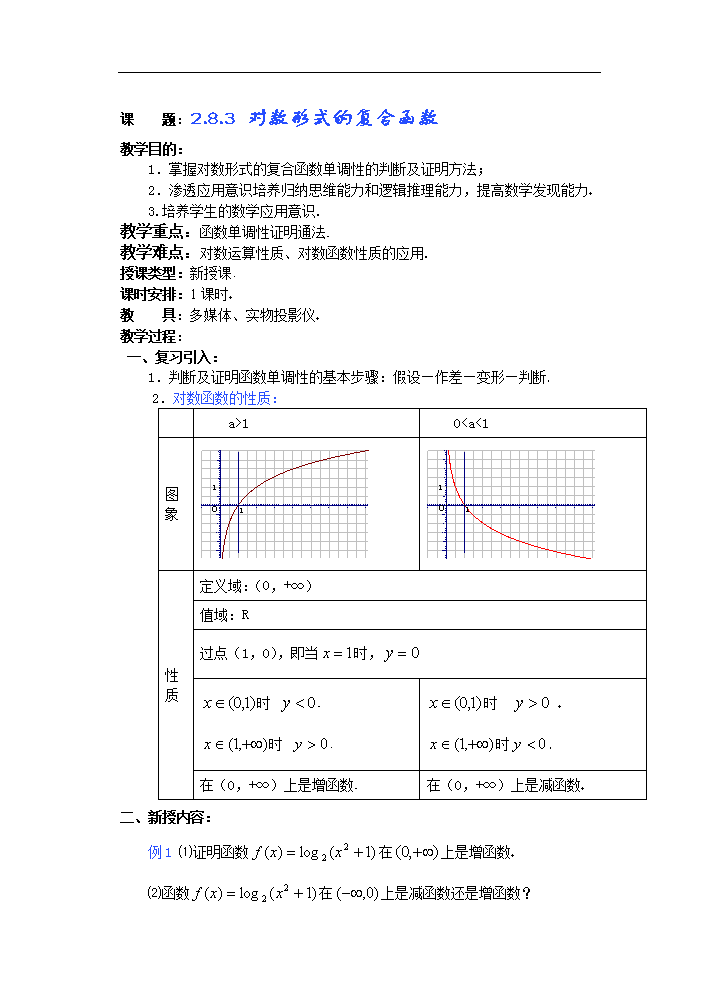
课 题:2.8.3 对数形式的复合函数 教学目的: 1.掌握对数形式的复合函数单调性的判断及证明方法; 2.渗透应用意识培养归纳思维能力和逻辑推理能力,提高数学发现能力 3.培养学生的数学应用意识. 教学重点:函数单调性证明通法 教学难点:对数运算性质、对数函数性质的应用. 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 1.判断及证明函数单调性的基本步骤:假设—作差—变形—判断 2.对数函数的性质: a>1 0查看更多
相关文章
- 当前文档收益归属上传用户