2020学年高一数学下学期期中试题（新版）人教版

2020学年高一数学下学期期中试题（新版）人教版

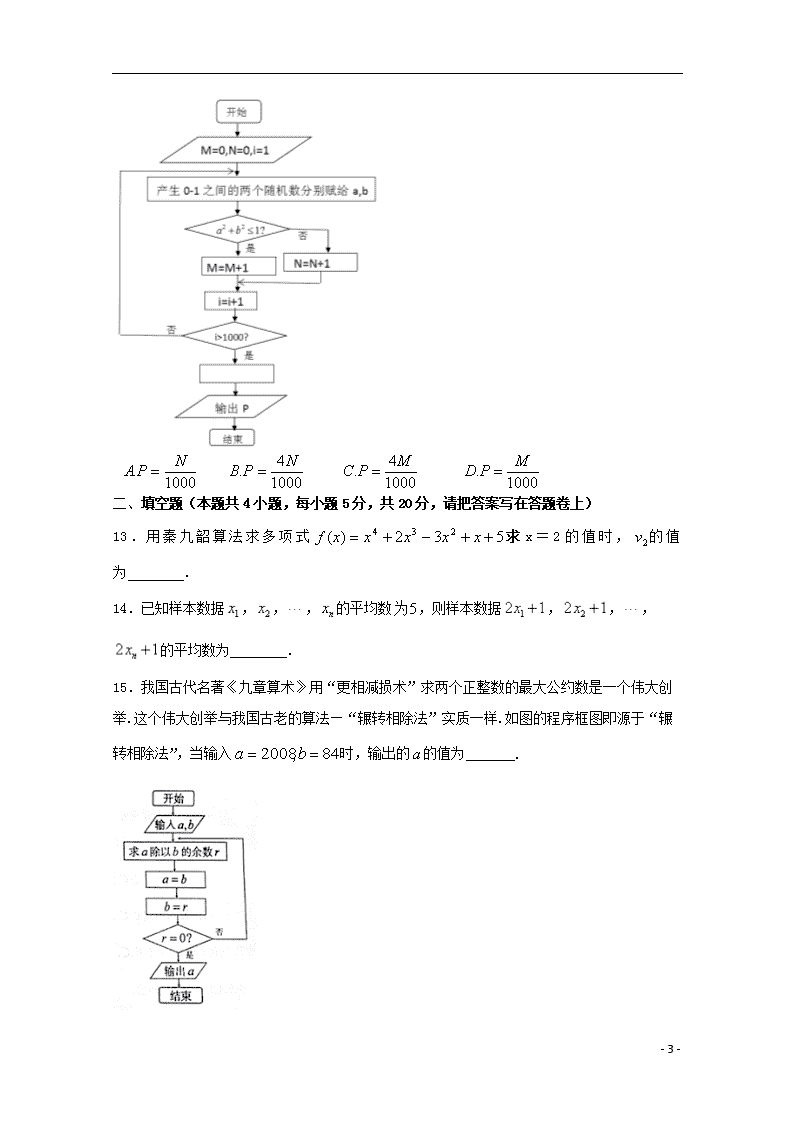
‎2019学年第二学期期中联考 高一 数学试卷 ‎【完卷时间：120分钟； 满分：150分】‎ 参考公式：1. 样本数据的方差：‎ ‎ ，其中为样本的平均数；‎ ‎ 2. 线性回归方程系数公式：‎ 一、选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写在答题卷上）‎ ‎1．下列给出的赋值语句中正确的是（ ） ‎ A． N=－N B. 3=A C.B=A=2 D.x+y=0‎ ‎2．二进制数化为十进制数的结果为（ ）‎ A． B． C． D．‎ ‎3．运行下面的程序，若输出的结果为9，则输入的值等于（ ）‎ A．1 B．2 C．3 D．4‎ ‎4．甲、乙两人下棋，两人下成和棋的概率是，甲获胜的概率是，则甲不输的概率为（ ）‎ ‎ A． B． C． D． 5． 九年级某班共有学生64人，座号分别为1,2,3,…,64现根据座号，用系统抽样的方法，抽取一个容量为4的样本．已知5号、21号、53号同学在样本中，那么样本中还有一个同学的座号是（ ）‎ - 11 -‎ ‎ A． 34 B．35 C．36 D．37‎ ‎6．一个容量为100的样本，其数据的分组与各组的频数如下：‎ 组别 ‎(0,10]‎ ‎(10,20]‎ ‎(20,30]‎ ‎(30,40]‎ ‎(40,50]‎ ‎(50,60]‎ ‎(60,70]‎ 频数 ‎12‎ ‎13‎ ‎24‎ ‎15‎ ‎16‎ ‎13‎ ‎7‎ 则样本数据落在(10,40]上的频率为( )‎ ‎ A．0.64 B．0.52 C．0.39 D．0.13 ‎ ‎7．在“世界读书日”前夕，为了了解某地名居民某天的阅读时间，从中抽取了名居民的阅读时间进行统计分析。在这个问题中，名居民的阅读时间的全体是（ ）‎ ‎ A. 样本的容量 B.个体 C. 总体 D.从总体中抽取的一个样本 ‎8．某学校为了调查学生的学习情况，由每班随机抽取名学生进行调查，若一班有名学生，将每一学生编号从到，请从随机数表的第行第、列（下表为随机数表的前行）的开始，依次向右，直到取足样本，则第6个样本编号为( )‎ 附随机数表：‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ ‎ A. B. C. D. ‎ ‎9．一箱产品中有正品4件，次品2件，从中任取2件，事件：‎ ‎①恰有1件次品和恰有2件次品； ②至少有1件次品和全是次品；‎ ‎③至少有1件正品和至少1件次品； ④至少有1件次品和全是正品.‎ 其中互斥事件为( )‎ ‎ A. ①③④ B. ①② C. ②③④ D. ①④‎ ‎10．下列说法：（1）频率是随机的，在试验前不能确定，随着试验次数的增加，频率一定会越来越接近概率 ‎（2）互斥事件不一定是对立事件，但是对立事件一定是互斥事件 ‎（3）在区间上随机选取一个数，则的概率为 ‎（4）从甲、乙等4名学生中随机选出2人，则甲被选中的概率为 其中不正确的个数是（ ） ‎ ‎ A.3 B.2 C.1 D.0‎ ‎11．某校早上8：00开始上课，假设该校学生小张与小王在早上7:30—7:50之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早10分钟到校的概率为（ ）‎ A. B. C. D.‎ ‎12．下图是用模拟方法估计圆周率π值的程序框图，P表示估计结果，则图中空白框内应填入（ ）‎ - 11 -‎ ‎ ‎ 二、填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上）‎ ‎13．用秦九韶算法求多项式求x＝2的值时，的值为 ．‎ ‎14．已知样本数据，，，的平均数，则样本数据，，，的平均数为 ．‎ ‎15．我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法—“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”，当输入时，输出的的值为 .‎ - 11 -‎ ‎16．“序数”指每个数字比其左边的数字大的自然数（如1258），在两位的“序数”中任取一个数比45大的概率是 .‎ 三、 解答题（本题共6个小题，共70分。解答应写出必要的文字说明、证明过程或演算步骤，请把答案写在答题卷上）‎ ‎17．（本小题满分10分）根据下面的要求，求值．‎ ‎（1）请完成执行该问题的程序框图；‎ ‎（2）以下是解决该问题的程序，请完成执行该问题的程序．‎ ‎ ‎ ‎18．（本小题满分12分）某种产品的广告费支出与销售额 - 11 -‎ ‎（单位：万元）之间有如下对应数据：‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ ‎（Ⅰ）用最小二乘法求关于的线性回归方程；‎ ‎（Ⅱ）试预估销售额为95.5万元时，广告费支出大约为多少万元？‎ 参考数据：‎ ‎19．（本小题满分12分）如下茎叶图记录了某CBA篮球队内两大中锋在六次训练中抢得篮板球数记录，由于教练一时疏忽，忘了记录乙球员其中一次的数据，在图中以X表示。‎ ‎（1）如果乙球员抢得篮板球的平均数为10时，求X的值和乙球员抢得篮板球数的方差；‎ ‎（2）如果您是该球队的教练在正式比赛中您会派谁上场呢？并说明理由（用数据说明）。‎ ‎20．（本小题满分12分）海关对同时从三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如右表所示，工作人员用分层抽样的方法从这些商品中共抽取6件进行检测 地区 数量 ‎50‎ ‎150‎ ‎100‎ ‎（1）求这6件样品中来自各地区商品的数量；‎ ‎（2）若在这6件样品中随机抽取2件送往甲机构进一步检测，求这2件商品来自不相同地区的概率.‎ - 11 -‎ ‎21．（本小题满分12分）某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5），[0.5,1），[4,4.5]分成9组，制成了如图所示的频率分布直方图.‎ ‎（I）求直方图中的a值；‎ ‎（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由；‎ ‎（Ⅲ）估计居民月均用水量的中位数.‎ - 11 -‎ ‎22．（本小题满分12分）某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：‎ 记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用（单位：元）,表示购机的同时购买的易损零件数.‎ ‎（I）若=19,求y与x的函数解析式；‎ ‎（II）若要求“需更换的易损零件数不大于”的频率不小于0.5,求的最小值；‎ ‎（III）假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件？‎ - 11 -‎ 福州市八县（市）协作校2016-2017学年第二学期期中联考 高一数学标准答案 一、选择题:‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B B C D B C A D D A C 二、填空题:‎ ‎13.5 14.11 15.4 16. ‎ 三、解答题:‎ ‎17.本题10分，每答对一空得一分。‎ ‎18．（本小题12分）‎ 解：（Ⅰ）由已知可得，， ……2分 ‎ - 11 -‎ ‎，，，‎ ‎，……6分 ‎，……7分 因此，所求回归直线方程是．……8分 ‎（Ⅱ）根据上面求得的线性回归方程，当销售额95.5万元时，95.5=6.5x+17.5 （万元），解得x=12,即这种产品的销售收入大约为12万元．…………… 12分 ‎19. （本小题12分）‎ 解: （1）依题意，得乙球员抢得篮板球数的平均数为10 ‎ 由茎叶图可得解得X=9 ……3分 乙球员抢得篮板球数的方差为 ‎……6分 ‎（2） ……8分 ‎ ‎ ‎ ……10分 因为 ……11分 由数据结果说明，乙球员发挥地更稳定，所以选派乙球员上场。……12分 ‎20．（本小题12分）‎ 解： (1)首先确定样本容量与总体中的个数的比是，‎ 从而得到样本中包含三个地区的个体数量分别是：‎ ，，. ……4分 ‎ ‎（2）设6件来自A，B，C三个地区的样品分别为,‎ 写出抽取的这2件商品构成的所有基本事件：‎ ，,‎ - 11 -‎ ,‎ ,共15个. ……9分 ‎ 记事件D：“抽取的这2件商品来自不相同地区”，‎ 写出事件D包含的基本事件：，,‎ 共11个 ……11分 ‎ 由每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的 ‎ …12分 备注：本题用对立事件也可以给分。‎ ‎21．（本小题12分）【答案】（Ⅰ）；（Ⅱ）36000；（Ⅲ）2.06.‎ 解：：（I）∵1=（0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04）×0.5，整理可得：2=1.4+2a， ∴解得：a=0.3. ……… 3分 ‎（II）估计全市居民中月均用水量不低于3吨的人数为3.6万，理由如下：‎ 由已知中的频率分布直方图可得月均用水量不低于3吨的频率为（0.12+0.08+0.04）×0.5=0.12， …………… 5分 又样本容量为30万，则样本中月均用水量不低于3吨的户数为30×0.12=3.6万．…………… 7分 ‎（Ⅲ）根据频率分布直方图，得；‎ ‎0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5=0.47＜0.5，‎ ‎0.47+0.5×0.52=0.73＞0.5，‎ ‎∴中位数应在（2，2.5]组内，设未知数为x+2，‎ 令0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5+0.50×x=0.5，‎ 解得x=0.04；∴中位数是2+0.04=2.04 …………… 12分 考点：频率分布直方图、中位数、平均数 ‎22. （本小题12分）‎ 解：（1）‎ ‎ ……4分 ‎（Ⅱ）由柱状图知,需更换的零件数不大于18的概率为0.06+0.16+0.24=0.46‎ ‎,不大于19的概率为0.46+0.24=0.7, 故的最小值为19. ……6分 - 11 -‎ ‎（Ⅲ）若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3800,20台的费用为4300,10台的费用为4800,因此这100台机器在购买易损零件上所需费用的平均数为:‎ ‎……9分 若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4000,10台的费用为4500,因此这100台机器在购买易损零件上所需费用的平均数为.‎ 比较两个平均数可知,购买1台机器的同时应购买19个易损零件. ……12分 - 11 -‎