- 2021-05-31 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一物理力的合成 力的分解人教实验版知识精讲(通用)
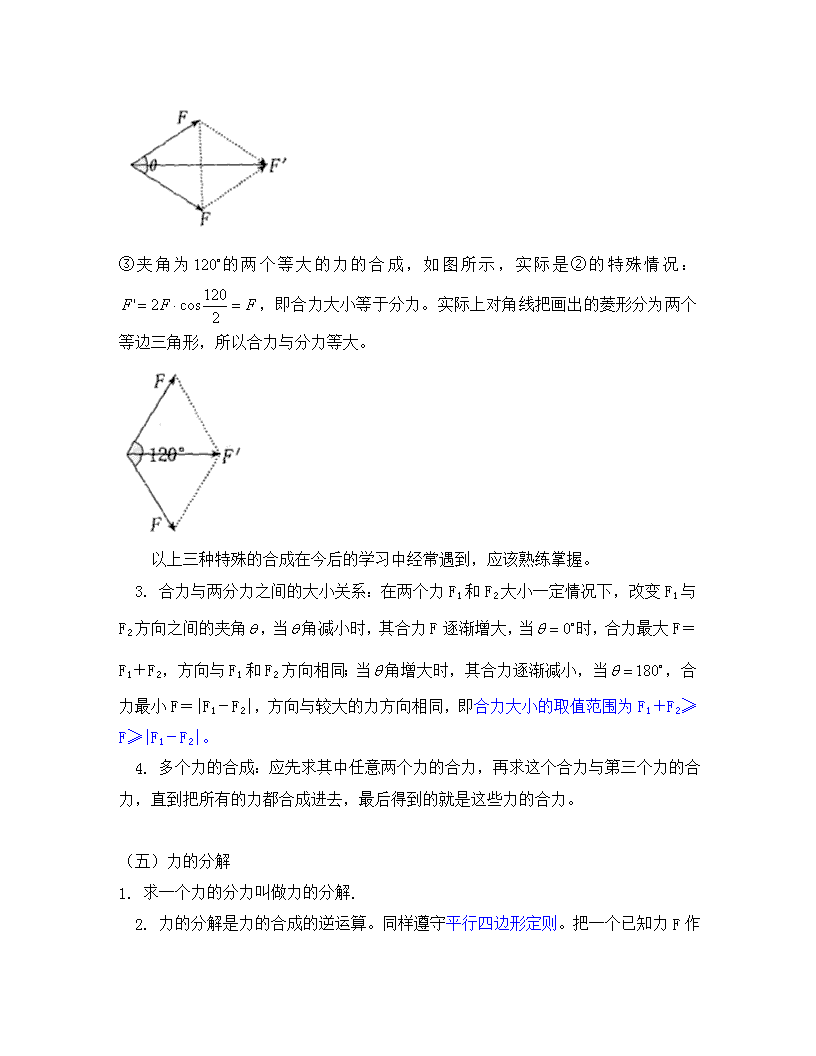
高一物理力的合成 力的分解人教实验版 【本讲教育信息】 一. 教学内容: 力的合成 力的分解 二. 知识要点: 1. 理解力的合成和合力的概念。 2. 掌握力的平行四边形定则。会用作图法求共点力的合力。 3. 理解力的分解和分力的概念,会用平行四边形定则解决力的分解问题。 4. 熟练掌握物体的受力分析,能够根据力的作用效果进行分解。 三. 重点、难点解析: (一)合力与分力 当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的效果相同,这个力就叫做那几个力的合力,原来几个力叫做分力。 (二)力的合成 1. 定义:求几个力的合力的过程或求合力的方法,叫做力的合成。 2. 平行四边形定则:两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。这个法则叫做平行四边形定则。 对力这种既有大小又有方向的物理量,进行合成运算时,一般不能用代数加法求合力,而必须用平行四边形定则。 (三)共点力 如果一个物体受到两个或更多力的作用,有些情况下这些力共同作用在同一点上,或者虽不作用在同一点,但它们的作用线交于一点,这样的一组力叫做共点力。平行四边形定则只适用于共点力的合成。 (四)讨论: 1. 力的合成的意义在于保证作用效果相同的前提下,用一个力的作用代替几个力的作用,这个力就是那几个力的“等效力”(合力)。力的平行四边形定则是运用“等效”观点,通过实验总结出来的共点力的合成法则,它给出了寻求这种“等效代换”所遵循的规律,作图法和计算法是运用这一规律进行共点力合成的具体方法。 (1)作图法:要选取统一标度,严格作出力的图示及平行四边形,量出平行四边形的对角线长度(注意是哪一条对角线),根据标度求出合力的大小,再量出对角线与某一分力的夹角,求出合力的方向。 (2)计算法:根据平行四边形定则作出力的示意图,然后利用解三角形的方式求出对角线,即为合力。 2. 力的合成的几种特殊情况: ①相互垂直的两个力的合成,如图所示,,合力F与分力F1的夹角的正切为:。 ②夹角为的两个等大的力的合成,如图所示,作出的平行四边形为菱形,利用其对角线互相垂直的特点可得直角三角形,解直角三角形求得合力,合力与每一个分力的夹角等于。 ③夹角为的两个等大的力的合成,如图所示,实际是②的特殊情况:,即合力大小等于分力。实际上对角线把画出的菱形分为两个等边三角形,所以合力与分力等大。 以上三种特殊的合成在今后的学习中经常遇到,应该熟练掌握。 3. 合力与两分力之间的大小关系:在两个力F1和F2大小一定情况下,改变F1与F2方向之间的夹角,当角减小时,其合力F逐渐增大,当时,合力最大F=F1+F2,方向与F1和F2方向相同;当角增大时,其合力逐渐减小,当,合力最小F=|F1-F2|,方向与较大的力方向相同,即合力大小的取值范围为F1+F2≥F≥|F1-F2|。 4. 多个力的合成:应先求其中任意两个力的合力,再求这个合力与第三个力的合力,直到把所有的力都合成进去,最后得到的就是这些力的合力。 (五)力的分解 1. 求一个力的分力叫做力的分解. 2. 力的分解是力的合成的逆运算。同样遵守平行四边形定则 。把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力F1、F2。 3. 作用在物体上的同一个力F可以分解为无数对大小、方向不同的分力。一般情况下我们按照力的作用效果进行分解。 (六)矢量相加的法则 1. 平行四边形定则:一切矢量(如力、位移等)相加遵从平行四边形定则。 2. 三角形定则:由两个矢量首尾相接与它们的合矢量组成一个三角形,从而求出合矢量,这个方法叫做三角形定则. 三角形定则与平行四边形定则的实质是一样的。 (七)矢量与标量 1. 矢量:既有大小又有方向,相加时遵从平行四边形定则(或三角形定则)。 2. 标量:只有大小,没有方向,求和时按照算术法则相加。 力的分解中定解条件的确定 将一个力F分解为两个分力,根据力的平行四边形定则,是以这个力F为平行四边形的一条对角线作一个平行四边形,在无附加条件限制时可作无数个不同的平行四边形,这说明两个力的合力可唯一确定,一个力的分力不是唯一的。要确定一个力的两个分力,一定有定解条件。 按力的效果进行分解,这实际上就是定解条件。如图的三角形支架,在节点O上施加一个力F,这个力产生两个效果:其一对AO有拉伸作用;其二对BO有挤压作用。将F分解为对OA的拉伸的力FAO和对BO挤压的力FBO,其定解条件是已知两个分力的方向。 按问题的需要进行分解,在解决具体问题时,根据具体问题对力进行分解。这个具体问题就是定解条件。如已确定两分力的大小,求分力的方向,两分力的大小是定解条件;已确定一个分力的大小、方向,求另一分力的大小、方向,这个已知分力为定解条件;已确定一个分力大小和另一分力的方向,求这一分力的方向和另一分力的大小,这个分力的大小和另一分力的方向为定解条件。 对力进行分解时,首先弄清定解条件,根据定解条件作出平行四边形图或三角形图,再依据几何知识求解。 力分解时有、无解的讨论 力分解时有解或无解,简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)。如果能构成平行四边形(或三角形),说明该合力可以分解成给定的分力,即有解。如果不能构成平行四边形(或三角形),说明该合力不能按给定的分力分解,即无解。具体情况有以下几种: 如何用三角形定则求矢量的变化量 矢量变化不仅大小变化,通常还有方向变化。求矢量的变化量实际上是求两矢量的差。求两矢量的和与差在表达形式上与代数和是相同的,只是在具体求的时候,将表达式中的和与差转换成用平行四边形定则或三角形定则求。如一个物体做曲线运动,它的初速度为v1,经过一段时间速度为v2,如图所示,求速度的变化量。速度的变化量是末速度v2与初速度v1的差,其数学表式为=v2-v1,但课本上讲的是矢量相加法则,如何将矢量相减变成矢量相加,我们不难发现,只要将上式变成v2=v1+就可以了。因此,只要将v1平移,使v2与v1的首端相接,从v1的末端向v2的末端做一条有向线段,该有向线段便是所求的速度变化量,如图所示。 【典型例题】 例1. 关于两个力的合力,下列说法错误的是 A. 两个力的合力一定大于每个分力 B. 两个力的合力可能小于较小的那个分力 C. 两个力的合力一定小于或等于两个分力 D. 当两个力大小相等时,它们的合力可能等于分力大小 解析:设分力F1与分力F2的夹角为,根据力的平行四边形定则,合力为F,以F1、F2为邻边的平行四边形所夹的对角线,如图所示。当时,F=F1+F2;当时,F=|F1-F2|,以上分别为合力F的最大值和最小值。当F1=F2且夹角时,合力F=0,小于任何一个分力,当F1=F2,夹角时,合力F =F1=F2,故本题的正确答案为AC。 答案:A C 例2. 在电线杆的两侧常用钢丝绳把它固定在地上(如图)。如果钢丝绳与地面的夹角,每条钢丝绳的拉力都是300N,求两根钢丝绳作用在电线杆上的合力。 解析:由图可知,两根钢丝绳的拉力F1和F2之间的夹角为,可根据平行四边形定则用作图法和解三角形法求出电线杆受到的合力。 方法一:作图法。 自O点引两条有向线段OC和OD,夹角为 。设定每单位长度表示100N,则OC和OD的长度都是3个单位长度,作出平行四边形OCED,其对角线OE就表示两个拉力F1、F2的合力F,量 得OE长为5.2个单位长度。 所以合力F=100×5.2N=520N 用量角器量得 所以合力方向竖直向下。 方法二:计算法。先画出力的平行四边形,如图所示,由于OC=OD,得到的是菱形。连结CD、OE,两对角线垂直且平分,OD表示300N,。在三角形中,。在力的平行四边形中,各线段的长表示力的大小,则有,所以合力 说明:力的合成有“作图法”和“计算法”,两种解法各有千秋。“作图法”形象直观,一目了然,但不够精确,误差大;“计算法”是用平行四边形先作图,再解三角形,似乎比较麻烦,但计算结果更准确 。今后我们遇到的求合力的问题,多数都用计算法,即根据平行四边形定则作出平行四边形后,通过解其中的三角形求合力。在这种情况下作的是示意图,不需要很严格,但要规范,明确哪些该画实线,哪些该画虚线,箭头应标在什么位置等。 例3. 物体受到三个力的作用,其中两个力的大小分别为5N和7N,这三个力的合力最大值为21N,则第三个力的大小为多少?这三个力的合力最小值为多少? 解析:当三个力的合力最大时,这三个力一定是在同一直线上,且方向相同,即合力F合=F1+F2+F3,则F3= F合-F1-F2=9N. 关于三个力的合力的最小值问题,有些同学仍受标量代数求和的干扰,不能真正理解矢量运算法则,而错误地认为合力最小值F’合=F1+F2-F3=3N,正确的方法应是:看三个力的大小是否能构成一个封闭三角形,即任取一个力,看这个力是否处在另外两个力的差和之间。若三个力满足上述条件,则合力的最小值为零;若不满足上述条件,则合力的最小值为较小的两个力先同方向合成,再和较大的一个力反方向合成的合力。 答案:第三个力大小是9N,三个力合力的最小值为零。 例4. 将一个力F分解为两个分力F1和F2,则下列说法中正确的是 A. F是物体实际受到的力 B. F1和F2两个分力在效果上可以取代力F C. 物体受到F1、F2和F三个力的作用 D. F是F1和F2的合力 解析:由分力和合力具有等效性可知B正确,分力F1和F2并不是物体实际受到的力,故A对C错。 答案:A、B、D 说明:合力与分力是一种等效替代关系,在力的合成中,分力是物体实际受到的力。在力的分解中,分力不是物体实际受到的力。 例5. 如图所示,电灯的重力G=10N,AO绳与顶板间夹角为 ,BO绳水平,则AO绳所受的拉力F1= ;BO绳所受的拉力F2= 。 解析:先分析物理现象:为什么绳AO、BO受到拉力呢?原因是由于OC绳的拉力产生了两个效果,一是沿AO向下的拉紧AO的分力Fl;二是沿BO向左的拉紧BO绳的分力F2,画出平行四边形,如图所示,因为OC拉力等于电灯重力,因此由几何关系得 , 答案:N 10N 说明:将一个已知力分解,在理论上是任意的,只要符合平行四边形定则就行,但在实际问题中,首先要弄清所分解的力有哪些效果,再确定各分力的方向,最后应用平行四边形定则求解。 例6. 在倾角的斜面上有一块竖直放置的挡板,在挡板和斜面之间放有一个重为G=20N光滑圆球,如图甲所示,试求这个球对斜面的压力和对挡板的压力。 解析:先分析物理现象,为什么挡板和斜面受压力呢?原因是球受到向下的重力作用,这个重力总是欲使球向下运动,但是由于挡板和斜面的支持,球才保持静止状态,因此球的重力产生了两个作用效果,如图乙所示,故产生两个分力:一是使球垂直压紧挡板的力F1,二是使球垂直压紧斜面的力F2;由几何关系得:,。F1和F2分别等于球对挡板和斜面的压力。 答案:, 说明:根据力实际产生的效果分解是同学们应该掌握的—项很重要的方法。 【模拟试题】 1. 关于合力与其两个分力的关系,下列说法正确的是 ( ) A. 合力的作用效果与两个分力的作用效果相同 B. 合力的大小一定等于两个分力大小之和 C. 合力可能小于它的任一个分力 D. 合力大小可能等于某一个分力的大小 2. 关于两个共点力的合力,下列说法中正确的是 ( ) A. 只要知道两个共点力的大小,合力就是唯一的 B. 已知两个共点力的大小和方向,合力就是唯一的 C. 已知一个力的大小和方向与另一个力的大小,合力就是唯一的 D. 已知一个力的大小和方向与另一个力的方向,合力就是唯一的 3. 物体同时受到同一平面内三个力作用,下列几组力的合力不可能为零的是 ( ) A. 5N,7N,8N B. 5N,2N,3N C. 1N,5N,10N D. 10N,10N,10N 4. 两个共点力的大小均为10N,如果要使这两个力的合力大小也是10N,则这两个共点力间的夹角应为 ( ) A. B. C. D. 5. 一个重为20N的物体置于光滑的水平面上,当用一个F=5N的力竖直向上拉该物体时,如图所示,物体受到的合力为 ( ) A. 15N B. 25N C. 20N D. 0N 6. 如图所示,物体M在斜向右下方的推力F作用下,在水平地面上恰好做匀速运动,则推力F和物体M受到的摩擦力的合力方向是 ( ) A. 竖直向下 B. 竖直向上 C. 斜向下偏左 D. 斜向下偏右 7. 如图所示,两个共点力F1、F2的大小一定,夹角是变化的,合力为F。在角从逐渐增大到的过程中,合力F的大小变化情况为 ( ) A. 从最小逐渐增加 B. 从最大逐渐减小到零 C. 从最大逐渐减小 D. 先增大后减小 8. 两个大小相等的共点力F1、F2,当它们间的夹角为时,合力大小为20N,则当它们间夹角为时,合力的大小为 ( ) A. 40N B. N C. N D. N 9. 两个共点力F1和F2的大小不变,它们 的合力F跟两力F1、F2之间的夹角的关系如图所示,则合力F大小的变化范围是 ( ) A. 0~1N B. 1~3N C. 1~5N D. 1~7N 10. 下列说法中正确的是 ( ) A. 一个力只能分解成惟一确定的一对分力 B. 同一个力可以分解为无数对大小、方向各不相同的分力 C. 已知一个力和它的一个分力,则另一个分力有确定值 D. 已知一个力和它的两个分力方向,则两分力有确定值 11. 将一个竖直向下的8N的力分解为两个力,其中一个分力方向水平,大小为6N,那么另一个分力大小为 ( ) A. 10N B. 8N C. 6N D. 2N 12. 对一个已知的力F进行分解,已知下面哪一个条件,它的解肯定是惟一的 ( ) A. 已知一个分力的大小和方向 B. 已知两个分力的方向 C. 已知一个分力的大小和另一个分力的方向 D. 已知一个分力的方向 13. 如图所示,一个半径为r,重为G的光滑均匀球,用长度为r的细绳挂在竖直光滑墙壁上,则绳子的拉力F和球对墙壁压力FN的大小分别是 ( ) A. G,G/2 B. 2G,G C. , D. , 14. 人站在岸上通过定滑轮用绳牵引低处的小船,如图所示,若水的阻力恒定不变,则在船匀速靠岸的过程中,下列说法正确的是 ( ) A. 绳的拉力不断增大 B. 绳的拉力保持不变 C. 船受到的浮力保持不变 D. 船受到的浮力不断减小 15. 如图所示,将力F(大小已知)分解为两个分力F1和F2,F2和F的夹角小于,则 ( ) A. 当时,肯定有两组解 B. 当时,肯定有两组解 C. 当时,有惟一一组解 D. 当时,无解 16. 两组能承受的最大拉力相等、长度不等的细线AO、BO,AO>BO按图所示悬挂一个中空的铁球,当在球内不断注入铁砂时,则 ( ) A. AO先被拉断 B. BO先被拉断 C. AO、BO同时被拉断 D. 条件不足,无法判断 17. 水平地面上斜放着一块木板AB,如图所示,在木板上放一木块,且处于静止状态,现使斜面的B端缓慢地放低,则木块所受弹力N,摩擦力的变化情况是 A. N增大,减小 B. N减小,增大 C. N减小,减小 D. N增大,增大 18. 如图所示,三角形轻支架ABC的边长AB=20cm,BC=15cm。在A点通过细绳悬挂一个重30N的物体,则AB杆受力大小为 N,AC杆受压力大小为 N。 19. 将18N竖直向下的力,分解为两个分力,其中一个分力沿水平方向,大小为24N,则另一个分力的大小是 N,方向与竖直方向的夹角是 。 20. 三个共点力的大小分别是5N、7N和14N,它们的合力最大值为 ,最小值是 ;若把14N的力改为10N,另两个力大小不变,它们的合力最大值为 ,最小值为 。 21. 如图所示,水平电线AB对竖直电线杆的拉力是30N,且只有斜牵引线BC与地面成角时,电线杆恰好竖直不偏转,试计算BC对电线杆的拉力。 22. 如图所示,用绳子AC和BC悬一重力为100N的物体,绳子AC和BC与天花板的夹角分别为和,求每条绳子的拉力分别是多少? 23. 如图所示,用悬绳AO、BO、CO悬挂一重物,AO、BO、CO所能承受的最大拉力均为100N,已知BO处于水平,AOB=,则为保证悬绳都不断,所挂重物最多不能超过多重? 【试题答案】 1. ACD 2. B 3. C 4. D 5. D 6. A 7. C 8. B 9. D 10. BCD 11. A 12. AB 13. D 14. AD 15. BD 16.B 17. A 18. 40,50 19. 30,53° 20. 26N,2N,22N,0 21. 50N 22. 50N,50N 23. 50N查看更多