高考上海文理科数学试卷及答案

高考上海文理科数学试卷及答案

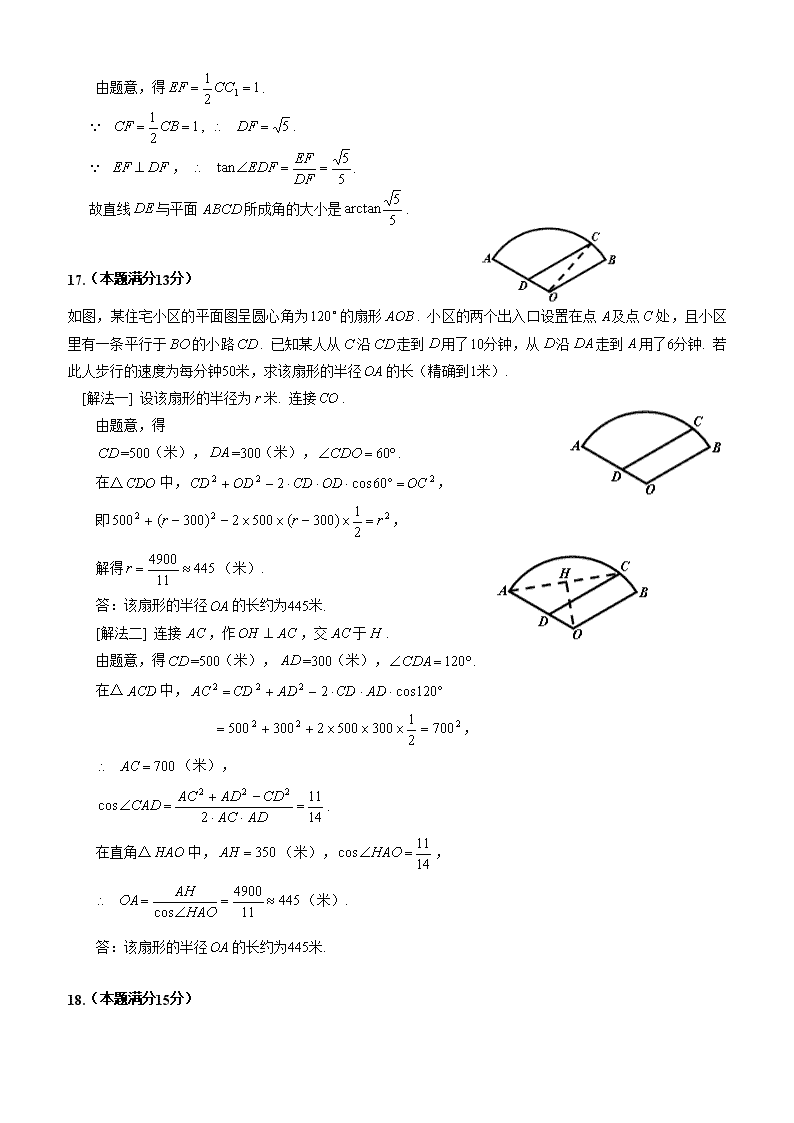
‎2 0 0 8 年 上海高考数学试卷(理)、（文）评析 一. 填空题（本大题满分44分）‎ ‎1．不等式的解集是 .‎ ‎2．若集合、满足，则实数=_____________.‎ ‎3．若复数满足（是虚数单位），则=_____.________.‎ ‎4．若函数的反函数为（），则 .‎ ‎5．若向量、满足，，且与的夹角为，则=__________.‎ ‎6．函数的最大值是 2. .‎ ‎7．在平面直角坐标系中，从六个点：、、、、、‎ ‎ 中任取三个，这三点能构成三角形的概率是 (结果用分数表示).‎ ‎8．设函数是定义在上的奇函数. 若当时，，则满足 的的取值范围是 .‎ ‎9．已知总体的各个体的值由小到大依次为2，3，3，7，，，12，13.7，18.3，20，且 ‎ 总体的中位数为. 若要使该总体的方差最小，则的取值分别是 ‎ ‎ .‎ ‎10．某海域内有一孤岛. 岛四周的海平面（视为平面）上有一浅水区（含边界），其边界 是长轴长为、短轴长为的椭圆. 已知岛上甲、乙导航灯的海拔高度分别为 ，且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上. 现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为，那么 船只已进入该浅水区的判别条件是 ‎ 解：‎ ‎11．方程的解可视为函数的图像与函数的图像交点的横坐标. 若方程的各个实根所对应的点()（=）均在直线的同侧，则实数的取值范围是 .‎ 解：方程的解可视为函数的图像与函数的图像交点的横坐标，由此可知：方程可变为：，先算：方程，‎ 则或 ‎（文）11．在平面直角坐标系中，点的坐标分别为、、. 如果是△围成的区域（含边界）上的点，那么当取到最大值时，点 的坐标是 ‎ 解：作图：由图可知点落在BC边时，有，‎ 则 当时，即点坐标为时，值最大。‎ 二. 选择题（本大题满分16分）‎ ‎12. 组合数恒等于 [答] ( D )‎ ‎ (A) . (B) . (C) . (D) .‎ ‎13. 给定空间中的直线及平面. 条件“直线与平面内无数条直线都垂直”是“直 线与平面垂直”的 [答] ( C )‎ ‎ (A) 充要条件. (B) 充分非必要条件. ‎ ‎ (C) 必要非充分条件. (D) 既非充分又非必要条件.‎ ‎14. 若数列是首项为1，公比为的无穷等比数列，且各项的和为，则 ‎ 的值是 [答] ( B )‎ ‎ (A) 1. (B) 2. (C) . (D) .‎ ‎15. 如图，在平面直角坐标系中，是一个与轴的正半轴、轴的正半轴分别相切于点 ‎、的定圆所围成的区域（含边界），是该 ‎ 圆的四等分点. 若点、点满足且， ‎ ‎ 则称优于. 如果中的点满足：不存在中的其它点优 ‎ 于，那么所有这样的点组成的集合是劣弧 [答] ( D )‎ ‎(A) . (B) . (C) . (D) .‎ 三. 解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．‎ ‎16.（本题满分12分）‎ ‎ 如图，在棱长为 2 的正方体中，的中点. 求直线与平面所成角的大小（结果用反三角函数值表示）. ‎ ‎[解] 过作，交于，连接.‎ ‎ ， ‎ ‎ 是直线与平面所成的角. ‎ ‎ 由题意，得.‎ ‎ , . ‎ ‎ ， . ‎ ‎ 故直线与平面所成角的大小是. ‎ ‎17.（本题满分13分）‎ 如图，某住宅小区的平面图呈圆心角为的扇形. 小区的两个出入口设置在点及点处，且小区里有一条平行于的小路. 已知某人从沿走到用了10分钟，从沿走到用了6分钟. 若此人步行的速度为每分钟‎50米，求该扇形的半径的长（精确到‎1米）. ‎ ‎ [解法一] 设该扇形的半径为米. 连接. ‎ 由题意，得 ‎=500（米），=300（米），. ‎ 在△中，， ‎ 即， ‎ 解得（米）. ‎ 答：该扇形的半径的长约为‎445米. ‎ ‎[解法二] 连接，作，交于. ‎ ‎ 由题意，得=500（米），=300（米），. ‎ ‎ 在△中，‎ ‎， ‎ ‎ （米）， ‎ ‎ . ‎ ‎ 在直角△中，（米），，‎ ‎ （米）. ‎ ‎ 答：该扇形的半径的长约为‎445米. ‎ ‎18.（本题满分15分）‎ ‎ 已知双曲线，是上的任意点.‎ ‎ （1）求证：点到双曲线的两条渐近线的距离的乘积是一个常数；‎ ‎ （2）设点的坐标为，求的最小值.‎ ‎（1）设是双曲线上任意一点，‎ ‎ 该双曲线的两条渐近线方程分别是和. ‎ ‎ 点到两条渐近线的距离分别是和 ‎ 它们的乘积是. ‎ ‎ 点到双曲线的两条渐近线的距离的乘积是一个常数. ‎ ‎ （2）设的坐标为，则 ‎ ‎ ‎ ‎ ‎ . ‎ ‎， ‎ ‎ 当时，的最小值为，‎ 即的最小值为. ‎ ‎（文）已知函数，直线与函数、的图像分别交于两点. ‎ ‎ （1）当时，求的值；‎ ‎ （2）求在 时的最大值.‎ ‎ [解] （1） ‎ ‎ . ‎ ‎ （2） ‎ ‎ ‎ ‎. ‎ ‎ ，， ‎ ‎ 的最大值为. ‎ ‎ ‎ ‎19.（本题满分16分）‎ ‎ 已知函数.‎ ‎ （1）若，求的值；‎ ‎ （2）若对于恒成立，求实数的取值范围.‎ ‎[解] （1）当时，；当时，. ‎ ‎ 由条件可知 ，即 ，‎ 解得 . ‎ ‎，. ‎ ‎ （2）当时，， ‎ 即 .‎ ‎， . ‎ ‎，‎ ‎ 故的取值范围是. ‎ ‎20.（本题满分16分）本题共有3个小题，第1小题满分3分，第2‎ ‎ 小题满分5分，第3小题满分8分．‎ ‎ ‎ 设是平面直角坐标系中的点，是经过原点与点的直线.记是直线与抛物线的异于原点的交点.‎ ‎ （1）已知. 求点的坐标；‎ ‎ （2）已知点在椭圆上，. 求证：点落在双曲线上；‎ ‎ （3）已知动点满足，. 若点始终落在一条关于轴对称的抛物线上，试问动点的轨迹落在哪种二次曲线上，并说明理由 ‎ [解]（1）当时，‎ ‎ 解方程组 得 ‎ ‎ 即点的坐标为. ‎ ‎ [证明]（2）由方程组 得 ‎ ‎ 即点的坐标为. ‎ ‎ 是椭圆上的点，即 ，‎ ‎ .‎ ‎ 因此点落在双曲线上. ‎ ‎ （3）设所在抛物线的方程为 ，. ‎ ‎ 将代入方程，得 ，即. ‎ 当时，，此时点的轨迹落在抛物线上；‎ 当时，，此时点的轨迹落在圆上； ‎ 当且时，，此时点的轨迹落在椭圆上；‎ 当时，，此时点的轨迹落在双曲线上. ‎ ‎ （文） 已知双曲线.‎ ‎ （1）求双曲线的渐近线方程；‎ ‎ （2）已知点的坐标为. 设是双曲线上的点，是点关于原点的对称点. 记. 求的取值范围；‎ ‎（3）已知点的坐标分别为，为双曲线上在第一象限内的点. ‎ 记为经过原点与点的直线，为△截直线所得线段的长. 试将表示为直线的斜率的函数.‎ ‎[解]（1）所求渐近线方程为. ‎ ‎ （2）设的坐标为，则的坐标为. ‎ ‎ ‎ ‎ . ‎ ‎ ,‎ ‎ 的取值范围是. ‎ ‎ （3）若为双曲线上第一象限内的点，‎ ‎ 则直线的斜率. ‎ 由计算可得，当时，；‎ 当时，. ‎ 表示为直线的斜率的函数是 ‎ ‎ ‎21.（本题满分18分）本题共有3个小题，第1小题满分3分，第 ‎ 2小题满分7分，第3小题满分8分．‎ ‎ 已知以为首项的数列满足：‎ ‎ （1）当，时，求数列的通项公式；‎ ‎ （2）当，时，试用表示数列前100项的和；‎ ‎ （3）当 （是正整数），，正整数时，求证：数列,‎ ‎，，成等比数列当且仅当.‎ ‎ （1）21. [解]（1）由题意得 . ‎ ‎ （2）当时，‎ ‎ ，，，，，，…，‎ ‎，，，… ‎ ‎ ‎ ‎ ‎ ‎ . ‎ ‎ （3）当时，；‎ ‎ ，； ‎ ‎ ，；‎ ‎ ，.‎ ‎ ，，，.‎ ‎ 综上所述，当时，数列，，，是公比为的等比数列. ‎ ‎ 当时， ， ‎ ‎ ，，‎ ‎ . ‎ 由于，，，‎ 故数列，，，不是等比数列.‎ ‎ 所以，数列，，，成等比数列当且仅当. ‎ ‎（文）已知数列：，，，（是正整数），与数列 ‎：，，，，（是正整数）. 记 ‎.‎ ‎ （1）若，求的值；‎ ‎ （2）求证：当是正整数时，；‎ ‎ （3）已知，且存在正整数，使得在，中有4项为100. 求的值，并指出哪4项为100.‎ ‎ [解]（1） ‎ ‎ ‎ ‎ . ‎ ‎ ，. ‎ ‎ [证明]（2）用数学归纳法证明：当时，. ‎ ‎ ① 当时，，等式成立. ‎ ‎ ② 假设时等式成立，即，‎ ‎ 那么当时， ‎ ‎ ‎ ‎ ‎ ‎ ，等式也成立. ‎ ‎ 根据①和②可以断定：当时，. ‎ ‎ [解]（3）(). ‎ ‎ 当时，；‎ ‎ 当时，；‎ ‎ 当时，；‎ ‎ 当时，；‎ ‎ 当时，；‎ ‎ 当时，. ‎ ‎ 是奇数，，，均为负数，‎ ‎ 这些项均不可能取到100. ‎ ‎ ，解得，，‎ ‎ 此时为100. ‎