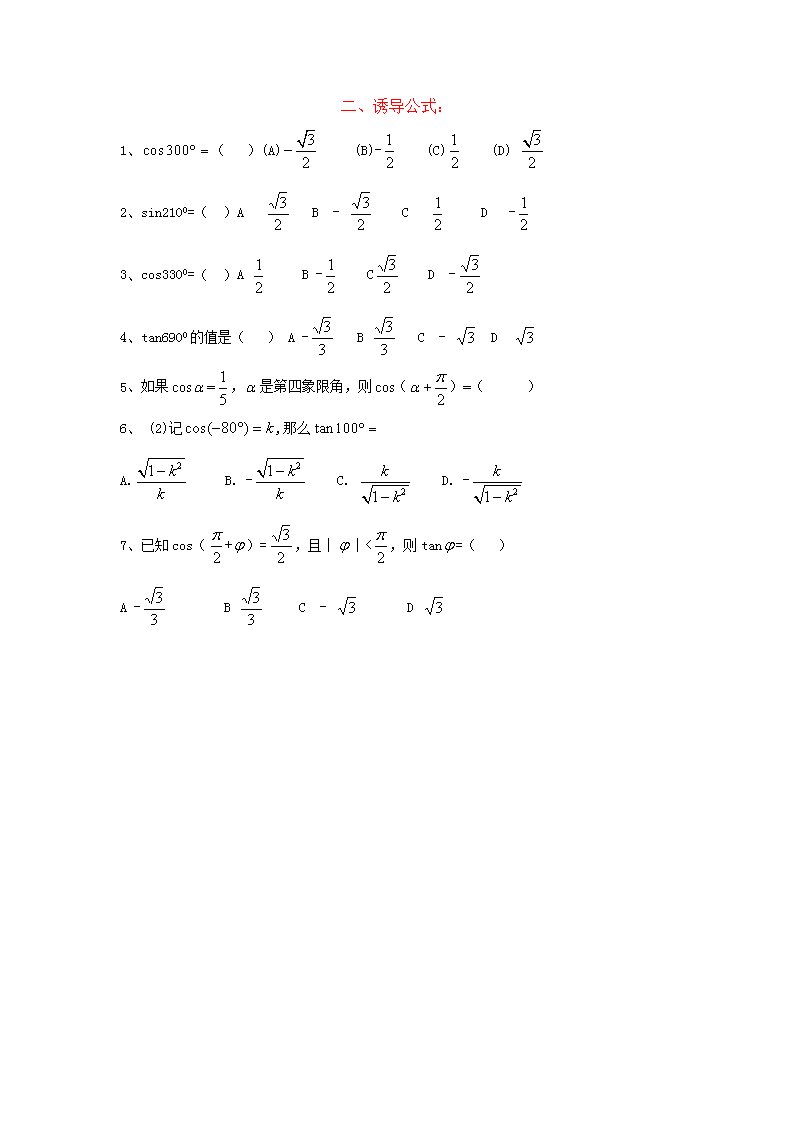高中数学必修四三角函数高考题汇编
必修四第一章三角函数高考题汇编
一、角的概念和同角关系:
1、已知是第三象限角,则所在的象限为( )
A 第一,二象限 B第二,三象限 C第一,三象限 D第二,四象限
2、已知costan<0,那么角是( )
A第一,二象限 B第二,三象限 C第三,四象限 D第一,四象限
3、如果的三个内角的余弦值分别等于的三个内角的正弦值,则( )
A.和都是锐角三角形
B.和都是钝角三角形
C.是钝角三角形,是锐角三角形
D.是锐角三角形,是钝角三角形
4、若cos>0且sin2<0,则角的终边所在象限是( )
A 第一象限 B第二象限 C第三象限 D第四象限
5、是第四象限角,cos=,则sin=( )
A B - C D -
6、已知sin=,<<,则tan=( )
7、是第四象限角,tan=-则sin=( )
A B - C D -
8、已知sin=则sin4- cos4的值是( )
A - B - C D
9、已知α是第二象限的角,tanα=1/2,则cosα=__________
二、诱导公式:
1、( )(A) (B)- (C) (D)
2、sin2100=( )A B - C D -
3、cos3300=( )A B - C D -
4、tan6900的值是( ) A - B C - D
5、如果cos=,是第四象限角,则cos(+)=( )
6、 (2)记,那么
A. B. - C. D. -
7、已知cos(+)=,且∣∣<,则tan=( )
A - B C - D
三、三角函数图像与性质:
1、函数y=1+cosx的图象( )
A关于x轴对称 B关于y轴对称 C关于原点对称 D关于直线x=对称
2、已知a∈R,函数y= sinx-∣a∣(x∈R)为奇函数,则a=( )
A 0 B 1 C -1 D
3、函数y=cos2x在下列哪个区间上是减函数( )
A [-,] B [,] C [0,] D [,]
4、已知函数y=sin(x-)-1,则下列命题正确的是( )
A f(x)是周期为1的奇函数 B f(x)是周期为2的偶函数
C f(x)是周期为1的非奇非偶函数 D f(x)是周期为2的非奇非偶函数
5、已知的定义在(0,3)上的函数,的图象如图所示,那么不等式的解集是( )
A.(0,1)∪(2,3) B. C. D.
6、已知是定义在上的奇函数,当时,的图象如图所示,那么不等式的解集是( )
(A) (B)
(C) (D)
7、下列函数中周期为的是( )
A y=sin B y=sin2x C y=cos D y=cos4x
8、设f(x)=sin3x+∣sin3x∣,则f(x)为( )
A 周期函数,最小正周期为 B 周期函数,最小正周期为
C周期函数,最小正周期为 2 D 非周期函数
9、函数y=5tan(2x+1)的最小正周期为( )
A B C D 2
10、下列函数中,周期为,且在上为减函数的是
(A) (B)(C) (D)
11、函数y=∣sinx∣的一个单调增区间是( )
A(-, ) B(,) C (,) D(,2)
12、已知函数y=∣sin(x+)∣(x∈R),则f(x)( )
A 在区间[,]上 是增函数 B 在区间[-,-]上 减函数
C 在区间[,]上 增函数 D在区间[,]上减函数
13、定义在R上的偶函数满足f(x)= f(x+2),当x∈[3,4] 时,
f(x)=x-2则( )
A f(sin)
f(cos)
C f(sin1)< f(cos1) D f(sin)>f(cos)
14、已知函数y=tan(x+),则( )
A f(0)> f(-1)>f(1) B f(0)>f(1)>f(-1)
C f(1)>f(0)>f(-1) D f(-1)>f(0)>f(1)
15、若动直线与函数和的图像分别交于两点,则的最大值为( )
A.1 B. C. D.2
16、10、定义在区间上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为________________________。
17、函数y=-xcosx的部分图象是( )
18、函数的图象大致是( )
19、函数的大致图象是( )
20、函数在区间内的图象是
21、已知函数,则的值域是
(A) (B) (C) (D)
22、设,,,则
(A) (B) (C) (D)
23、在同一平面直角坐标系中,函数的图象和直线的交点个数是
(A)0 (B)1 (C)2 (D)4
24、(05上海)函数的图象f(x)=sinx+2∣sinx∣,x∈[0,2]与直线y=k有且只有两个不同的交点,则k的取值范围是( )
25、若0≤x<2且=sinx-cosx, 则( )
A 0≤x≤ B ≤x≤ C ≤x≤ D ≤x≤
26、定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是,且当x∈[0,]时,f(x)= sinx,则f()的值( )
A - B C - D
四、y=Asin(ωx+φ)(ω>0)的图像与性质
1、函数f(x)= 的最小正周期为
A. B.x C.2 D.4
2、函数y=2sin(-2x)(x∈[0,])为增函数的区间是( )
A [0,] B [,] C [,] D [,]
3、已知函数f(x)=sin(x+)(>0)的最小正周期T是,则该函数图象( )
A关于点(,0)对称 B关于直线x=对称
C关于点(,0)对称 D关于直线x=对称
4、函数f(x)=tan(x+)的单调递增区间为( )
A (k-, k+)B(k, k+)C (k-, k+) D(k-, k+)
5、函数f(x)=3sin(2x-)的图象为C,①图象C关于直线x=对称;②函数f(x)在(-,)内是增函数;③由y=3sin2x的图象向右平移个单位长度可以得到图象C。以上三个论断中,正确 的论断个数是( )
A 0 B 1 C 2 D 3
6、已知函数f(x)=2sinx(>0)在区间[-,]上的最小值是-2,则的最小值是( )
A B C 2 D 3
7、已知简谐运动f(x)=2sin(x+)(∣∣<)的图象经过点(0,1),则该简谐运动的最小正周期T和初相分别为( )
A T=6, = B T=6,= C T =6,= DT=6,=
8、若函数 (ω>0)在区间上单调递增,在区间上单调递减,则ω=
A.3 B.2 C. D.
9、已知函数f(x)=sin(x+)(x∈R,>0,∣∣<)的最小正周期T是,且f(0)=,则( )
A =,= B = ,= C =2,= D =2,=
10、设点p是函数f(x)=sinx的图象C的一个对称中心,若点p到图象C的对称轴的距离的最小值是,则函数f(x)的最小正周期是( )
A 2 B C D
11、已知,且在区间有最小值,无最大值,则=__________.
12、已知函数和的图象的对称轴完全相同。若,则的取值范围是 。
13、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( B )
A. 1 B. 2
C. 1/2 D. 1/3
14、已知函数,其中为实数,若对恒成立,且 ,则的单调递增区间是
(A) (B)
(C) (D)
15、(9)设函数,则在下列区间中函数不存在零点的是
(A) (B) (C) (D)
16、(7)为了得到函数的图像,只需把函数的图像
(A)向左平移个长度单位 B)向右平移个长度单位
(C)向左平移个长度单位 (D)向右平移个长度单位
17、(6)设,函数的图像向右平移个单位后与原图像重合,则的最小值是
(A) (B) (C) (D) 3
18、将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
A)B) C)D)
19、为了得到这个函数的图象,只要将的图象上所有的点
(A)向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
(B) 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
(C) 向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
(D) 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
20、将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
A) B)C) D)
21、设函数,将的图像向右平移个单位长度后,所得的图像与原图像重合,则的最小值等于
A. B. C. D.
22、要得到函数y=sinx的图象,只需将函数y=cos(x-)的图象( )
A向右平移单位 B向右平移单位 C向左平移单位 D向左平移单位
23、为得到函数的图像,只需将函数的图像( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
24、把函数()的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象表示函数是
(A), (B),
(C), (D),
25、将函数的图象按向量平移后所得的图象关于点中心对称,则向量的坐标可能为( )
A. B. C. D.
26、将函数的图象F按向量平移得到图象,若的一条对称轴是直线,则的一个可能取值是
A. B. C. D.
27.为了得到函数的图像,只需把函数的图像上所有的点
(A)向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
(B)向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
(C)向左平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
28.要得到函数的图象,只需将函数
的图象上所有的点的
(A)横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
(B)横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
(C)横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度
(D)横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度
29.为了得到函数的图象,可以将函数的图象( )
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
30、要得到函数y=cosx的图象,只需将函数y=sin(2x+)的图象上所有点( )
A 横坐标缩短到原来的倍,再向左平移个单位
B横坐标缩短到原来的倍,再向右平移个单位
C 横坐标伸长到原来的2倍,再向左平移个单位
D横坐标伸长到原来的2倍,再向右平移个单位
31、将y=2cos(+)的图象先向左平移个单位,再向下平移2个单位,则平移后所得图象的解析式为( )
A y=2cos(+)-2 B y=2cos(-)+2
C y=2cos(-)-2 D y=2cos(+)+2
32、下列有五个命题:①函数y=sin4x-cos4x的最小正周期是;②终边在y上的集合是﹛∣=,k∈Z﹜;③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点④把函数y=3sin(2x+)的图象向右平移个单位长度得到y=3sin2x的图象 ;⑤函数y=sin(x-)在[0,]上的减函数。其中真命题的编号是( )
33、已知函数的部分图象如图所示,则
A. =1 = B. =1 =-
C. =2 = D. =2 = -
34、已知函数=Atan(x+)(),y=的部分图像如下图,则 .
35、函数是常数,的部分图象如图所示,则f(0)= ___________________
36、(06四川)下列函数中,图象的一部分如图的是( )
A y=sin(x+) By=sin(2x-) C y=cos(4x-) Dy=cos(2x-)
37、函数的部分图象如图,则
A. B.C. D.
38、函数y=A(sinwx+j)(w>0,,xÎR)的部分图象如图所示,则函数表达式为 ( )
(A) (B)
(C) (D)
39、若函数的图象(部分)如图所示,则的取值是
A. B.
C. D.
40、如图,函数y=2sin(πx+φ),x∈R,(0≤φ≤)的图象与y轴交于点(0,1).
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求
41、已知函数上的偶函数,其图象关于点对称,且在区间上是单调函数求的值
42、设函数图像的一条对称轴是直线。
(Ⅰ)求;
(Ⅱ)求函数的单调增区间;
(Ⅲ)画出函数在区间上的图像。
(Ⅳ)证明直线与函数的图像不相切。