高考物理一轮总复习 必修部分 相互作用 重力 弹力 摩擦力限时规范特训

高考物理一轮总复习 必修部分 相互作用 重力 弹力 摩擦力限时规范特训

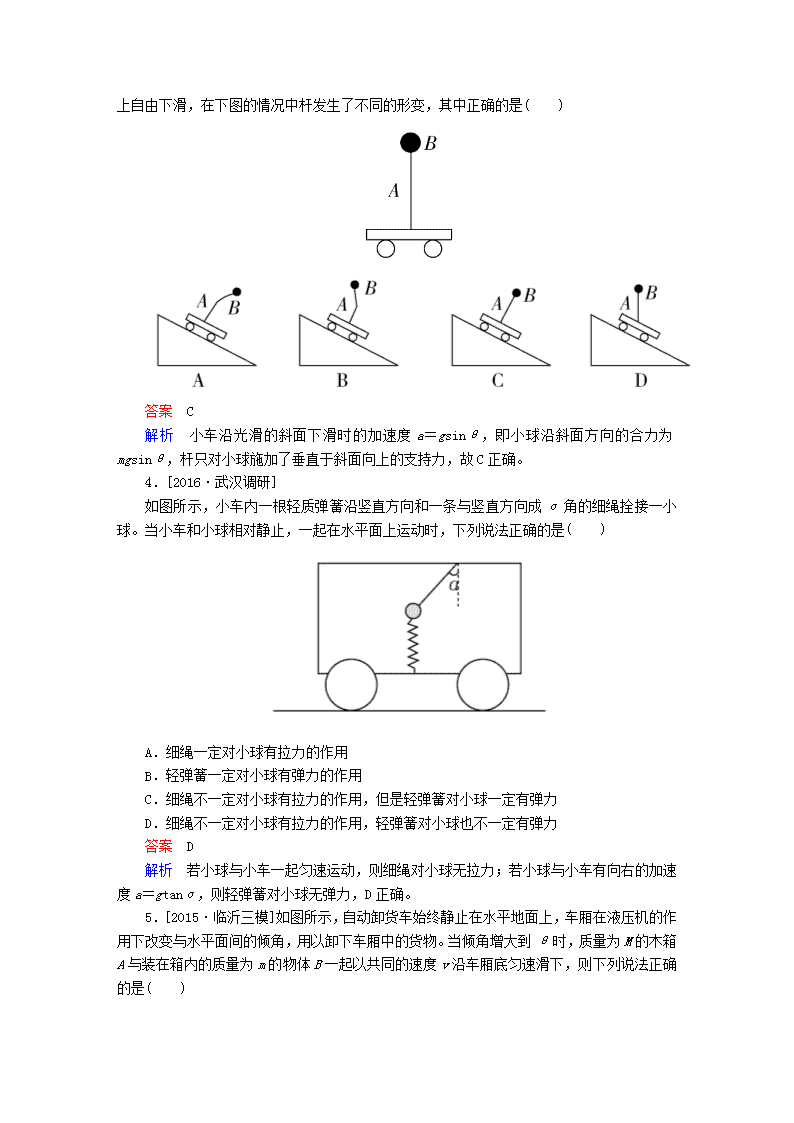
第1讲 重力 弹力 摩擦力 ‎　　时间：45分钟　满分：100分 一、选择题(本题共13小题，每小题6分，共78分。其中1～9为单选，10～13为多选)‎ ‎1．如图所示，两辆车在以相同的速度做匀速运动，根据图中所给信息和所学知识你可以得出的结论是(　　)‎ A．物体各部分都受重力作用，但可以认为物体各部分所受重力集中于一点 B．重力的方向总是垂直向下的 C．物体重心的位置与物体形状或质量分布无关 D．力是使物体运动的原因 答案　A 解析　物体各部分都受重力作用，但可以认为物体各部分所受重力集中于一点，这个点就是物体的重心，重力的方向总是和水平面垂直，是竖直向下而不是垂直向下，所以选项A正确，B错误；从图中可以看出，汽车(包括货物)的形状和质量分布发生了变化，重心的位置就发生了变化，故选项C错误；力不是使物体运动的原因而是改变物体运动状态的原因，所以选项D错误。‎ ‎2．[2015·雅礼模拟]质量为mA和mB的小球与劲度系数均为k的轻弹簧L1和L2连接如图，静止时，两弹簧伸长量分别为x1和x2，则(　　)‎ A．只要mA＝mB，有x1＝x2‎ B．只要mA>mB，有x1x2‎ 答案　D 解析　由于kx2＝mBg，kx1＝(mA＋mB)g，故x1>x2，所以选项D对。‎ ‎3．小车上固定一根弹性直杆A，杆顶固定一个小球B ‎(如图所示)，现让小车从光滑斜面上自由下滑，在下图的情况中杆发生了不同的形变，其中正确的是(　　)‎ 答案　C 解析　小车沿光滑的斜面下滑时的加速度a＝gsinθ，即小球沿斜面方向的合力为mgsinθ，杆只对小球施加了垂直于斜面向上的支持力，故C正确。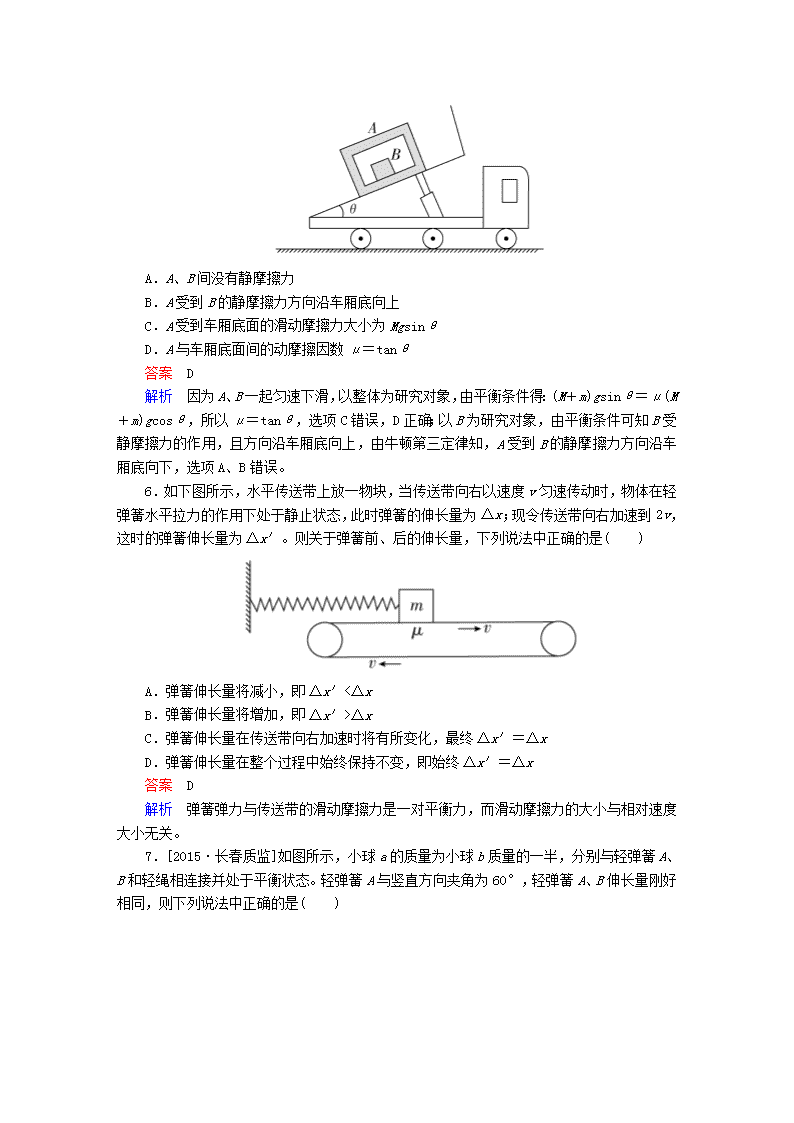‎ ‎4．[2016·武汉调研] ‎ 如图所示，小车内一根轻质弹簧沿竖直方向和一条与竖直方向成α角的细绳拴接一小球。当小车和小球相对静止，一起在水平面上运动时，下列说法正确的是(　　)‎ A．细绳一定对小球有拉力的作用 B．轻弹簧一定对小球有弹力的作用 C．细绳不一定对小球有拉力的作用，但是轻弹簧对小球一定有弹力 D．细绳不一定对小球有拉力的作用，轻弹簧对小球也不一定有弹力 答案　D 解析　若小球与小车一起匀速运动，则细绳对小球无拉力；若小球与小车有向右的加速度a＝gtanα，则轻弹簧对小球无弹力，D正确。‎ ‎5．[2015·临沂三模]如图所示，自动卸货车始终静止在水平地面上，车厢在液压机的作用下改变与水平面间的倾角，用以卸下车厢中的货物。当倾角增大到θ时，质量为M的木箱A与装在箱内的质量为m的物体B一起以共同的速度v沿车厢底匀速滑下，则下列说法正确的是(　　)‎ A．A、B间没有静摩擦力 B．A受到B的静摩擦力方向沿车厢底向上 C．A受到车厢底面的滑动摩擦力大小为Mgsinθ D．A与车厢底面间的动摩擦因数μ＝tanθ 答案　D 解析　因为A、B一起匀速下滑，以整体为研究对象，由平衡条件得：(M＋m)gsinθ＝μ(M＋m)gcosθ，所以μ＝tanθ，选项C错误，D正确；以B为研究对象，由平衡条件可知B受静摩擦力的作用，且方向沿车厢底向上，由牛顿第三定律知，A受到B的静摩擦力方向沿车厢底向下，选项A、B错误。‎ ‎6．如下图所示，水平传送带上放一物块，当传送带向右以速度v匀速传动时，物体在轻弹簧水平拉力的作用下处于静止状态，此时弹簧的伸长量为Δx；现令传送带向右加速到2v，这时的弹簧伸长量为Δx′。则关于弹簧前、后的伸长量，下列说法中正确的是(　　)‎ A．弹簧伸长量将减小，即Δx′<Δx B．弹簧伸长量将增加，即Δx′>Δx C．弹簧伸长量在传送带向右加速时将有所变化，最终Δx′＝Δx D．弹簧伸长量在整个过程中始终保持不变，即始终Δx′＝Δx 答案　D 解析　弹簧弹力与传送带的滑动摩擦力是一对平衡力，而滑动摩擦力的大小与相对速度大小无关。‎ ‎7．[2015·长春质监]如图所示，小球a的质量为小球b质量的一半，分别与轻弹簧A、B和轻绳相连接并处于平衡状态。轻弹簧A与竖直方向夹角为60°，轻弹簧A、B伸长量刚好相同，则下列说法中正确的是(　　)‎ A．轻弹簧A、B的劲度系数之比为3∶1‎ B．轻弹簧A、B的劲度系数之比为2∶1‎ C．轻绳上拉力与轻弹簧A上拉力大小之比为2∶1‎ D．轻绳上拉力与轻弹簧B上拉力大小之比为1∶1‎ 答案　A 解析　设两弹簧的伸长量都为x，a的质量为m，对小球b受力分析，由平衡条件可得：弹簧B的弹力kBx＝2mg，对小球a受力分析，可得：kBx＋mg＝kAxcos60°，联立可得：kA＝3kB，选项A正确，B错误；同理轻绳上拉力F＝kAxsin60°＝kAx＝kBx，选项C、D错误。‎ ‎8．[2015·福建四地六校联考]如图，A、B两物体叠放在水平地面上，A物体质量m＝‎20 kg，B物体质量M＝‎30 kg。处于水平位置的轻弹簧一端固定于墙壁，另一端与A物体相连，弹簧处于自然状态，其劲度系数为250 N/m，A与B之间、B与地面之间的动摩擦因数均为μ＝0.5。现用一水平推力F作用于物体B上，使B缓慢地向墙壁移动，A、B始终保持相对静止。当B移动‎0.2 m时，水平推力的大小为(g取‎10 m/s2)(　　)‎ ‎　‎ A．200 N B．250 N C．300 N D．350 N 答案　C 解析　B相对地面移动，B与地面之间为滑动摩擦力，大小f＝μ(M＋m)g＝250 N，因缓慢移动，故受力平衡，F＝kx＋f，代入数据F＝300 N，故C正确，A、B、D错误。‎ ‎9．如图所示，质量为‎1 kg的物体与地面间的动摩擦因数μ＝0.2，从t＝0开始以初速度v0沿水平地面向右滑行，同时受到一个水平向左的恒力F＝1 N的作用，g取‎10 m/s2，向右为正方向，该物体受到的摩擦力f随时间变化的图象是(最大静摩擦力等于滑动摩擦力)(　　)‎ 答案　A 解析　物体在力F和摩擦力作用下向右做匀减速直线运动，此时滑动摩擦力水平向左，大小为Ff1＝μmg＝2 N，物体的速度为零后，物体在力F作用下处于静止状态，物体受水平向右的静摩擦力，大小为Ff2＝F＝1 N，故只有图A正确。‎ ‎10．如图所示，在探究摩擦力的实验中，用弹簧测力计水平拉一放在水平桌面上的小木块，小木块的运动状态和弹簧测力计的读数如下表所示(每次实验时，木块与桌面的接触面相同)，则由下表分析可知，下列选项正确的是(　　)‎ 实验次数 小木块的运动状态 弹簧测力计读数/N ‎1‎ 静止 ‎0.4‎ ‎2‎ 静止 ‎0.6‎ ‎3‎ 直线加速 ‎0.7‎ ‎4‎ 匀速直线 ‎0.5‎ ‎5‎ 直线减速 ‎0.3‎ A.木块受到的最大静摩擦力为0.7 N B．木块受到的最大静摩擦力可能为0.6 N C．在这五次实验中，木块受到的摩擦力大小有三次是相同的 D．在这五次实验中，木块受到的摩擦力大小各不相同 答案　BC 解析　第1次和第2次实验都没有拉动木块，说明这两次的拉力大小均未超过最大静摩擦力，第三次实验时，木块做加速运动，说明拉力已经大于最大静摩擦力Fm，因此可知，最大静摩擦力范围0.6 N≤Fm<0.7 N，故A错、B对；滑动摩擦力与运动情况无关，因此第3、4、5次的摩擦力大小相等，故C对、D错。‎ ‎11．如图所示，有一个重力不计的正方形容器，被水平力F压在竖直的墙面上处于静止状态，现缓慢地向容器内注水，直到将容器刚好盛满为止，在此过程中容器始终保持静止，则下列说法中正确的是(　　)‎ A．容器受到的摩擦力不变 B．容器受到的摩擦力逐渐增大 C．水平力F可能不变 D．水平力F必须逐渐增大 答案　BC 解析　容器始终保持静止，竖直方向重力平衡静摩擦力，因重力变大，则静摩擦力变大。水平力F决定最大静摩擦力，只要重力小于等于最大静摩擦力，容器静止，所以F不一定变大，可能不变。‎ ‎12．如图甲、乙所示，倾角为θ的斜面上放置一滑块M，在滑块M上放置一个质量为m的物块，M和m相对静止，一起沿斜面匀速下滑，下列说法正确的是(　　)‎ A．图甲中物块m受到摩擦力 B．图乙中物块m受到摩擦力 C．图甲中物块m受到水平向左的摩擦力 D．图乙中物块m受到与斜面平行向上的摩擦力 答案　BD 解析　对图甲：设m受到摩擦力，则物块m受到重力、支持力、摩擦力，而重力、支持力平衡，若受到摩擦力作用，其方向与接触面相切，方向水平，则物体m受力将不平衡，与题中条件矛盾，故假设不成立，A、C错误。对图乙：设物块m不受摩擦力，由于m匀速下滑，m必受力平衡，若m只受重力、支持力作用，由于支持力与接触面垂直，故重力、支持力不可能平衡，则假设不成立，由受力分析知乙图中m受到沿斜面向上的摩擦力。‎ ‎13．如图所示，A、B、C 三个物体质量相等，它们与传送带间的动摩擦因数相同。三个物体随传送带一起匀速运动，运动方向如图中箭头所示。则下列说法正确的是(　　)‎ A．A物体受到的摩擦力不为零，方向向右 B．三个物体只有A物体受到的摩擦力为零 C．B、C受到的摩擦力大小相等，方向相同 D．B、C受到的摩擦力大小相等，方向相反 答案　BC 解析　A物体与传送带一起匀速运动，没有发生相对滑动，也没有相对运动趋势，所以A物体不受摩擦力，选项A错误；对B、C物体进行受力分析，可知B、C所受的静摩擦力大小均等于mgsinθ，方向均沿传送带向上，选项B、C正确，D错误。‎ 二、非选择题(本题共22分)‎ ‎14．如图所示，质量为m的物体与A、B两个弹簧相连，其劲度系数分别为k1和k2，B弹簧下端与地相连，现用手拉A的上端，使A缓慢上移，当B弹簧的弹力为原来的2/3时，A上端移动的距离是多少？‎ 答案　mg或mg 解析　B原来处于压缩状态，其压缩量为x0＝mg/k2，当向上缓慢拉A使B中弹力减为原来的2/3时，有两种可能：‎ ‎(1)B仍处于被压缩的状态，则此时A弹簧的弹力和伸长量分别为 F1＝mg－F2＝mg，x1＝F1/k1＝ 这时B上端移动的位移x2＝＝mg/k2＝ 所以A上端移动的距离 sA＝x1＋x2＝mg ‎(2)B处于拉伸状态，则此时A的弹力和伸长量分别为 F1′＝mg＋F2′＝mg，x1′＝F1′/k1＝mg 这时B上端移动的位移 x2′＝ΔF2′/k2＝mg 所以A上端上移的距离为 sA′＝x1′＋x2′＝mg