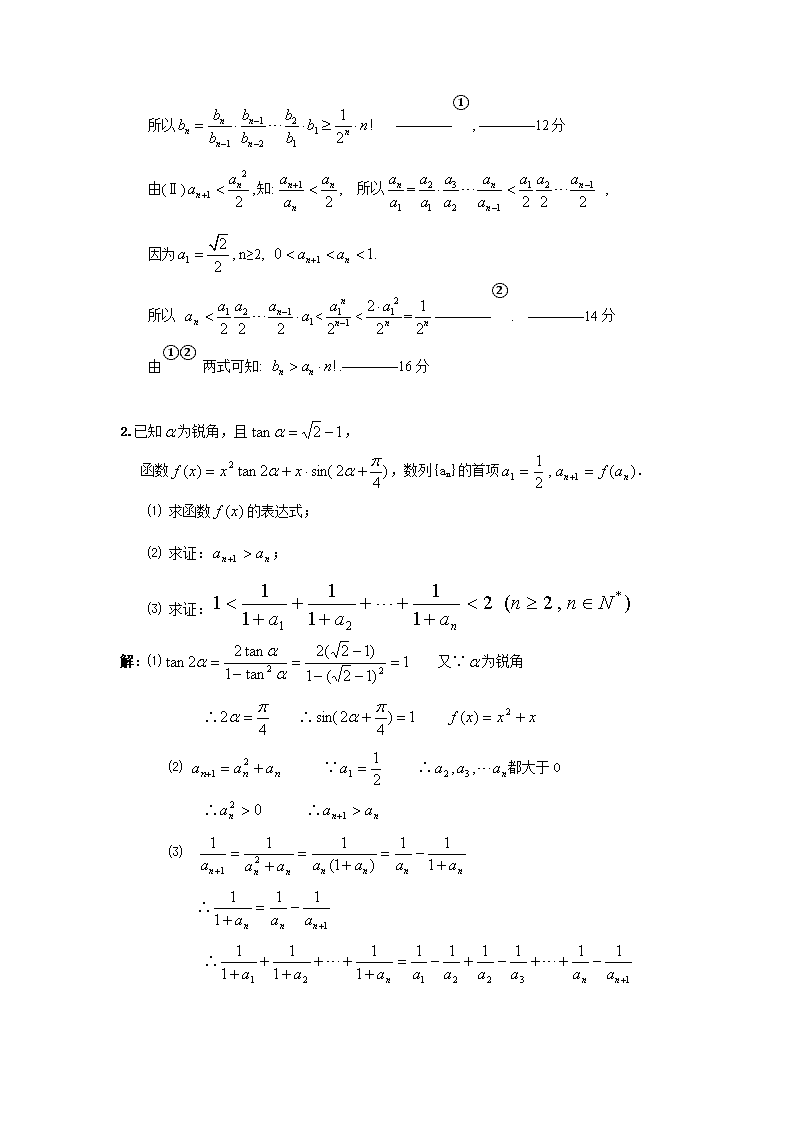高考模拟热点交汇试题汇编之数列与不等式
高考模拟热点交汇试题汇编之数列与不等式（30题）
（命题者的首选资料）
1. 已知函数,数列满足,
; 数列满足, .求证:
（Ⅰ）
（Ⅱ）
（Ⅲ）若则当n≥2时,.
解: (Ⅰ)先用数学归纳法证明,.
（1）当n=1时,由已知得结论成立;
（2）假设当n=k时,结论成立,即.则当n=k+1时,
因为0
g(0)=0.
因为,所以,即>0,从而————10分
(Ⅲ) 因为 ,所以, ,
所以 ————① , ————12分
由(Ⅱ)知:, 所以= ,
因为, n≥2,
所以 <<=————② . ————14分
由①② 两式可知: .————16分
2.已知为锐角，且，
函数，数列{an}的首项.
⑴ 求函数的表达式；
⑵ 求证：；
⑶ 求证：
解：⑴ 又∵为锐角
∴ ∴
⑵ ∵ ∴都大于0
∴ ∴
⑶
∴
∴
∵, , 又∵
∴ ∴
∴
3.（本小题满分14分）已知数列满足
（Ⅰ）求数列的通项公式；
（Ⅱ）若数列满足，证明：是等差数列；
（Ⅲ）证明：
解：（1），……………………2分
故数列是首项为2，公比为2的等比数列。……………………3分
，…………………………………………4分
（2），……………5分
①
②
②—①得，即③……………………8分
④
④—③得，即……………………9分
所以数列是等差数列
（3）………………………………11分
设，则
…………13分
………………………………14分
4.设（e为自然对数的底数）
（I）求p与q的关系；
（II）若在其定义域内为单调函数，求p的取值范围；
（III）证明：
①；
②（n∈N，n≥2）.
解：（I）由题意
（II）由（I）知：
令h(x)=px2－2x+p.要使g(x)在（0，+∞）为单调函数，只需h(x)在（0，+∞）满足：
h(x)≥0或h(x)≤0恒成立.………………………………4分
①，
∴g(x)在（0，+∞）单调递减，
∴p=0适合题意.………………………………………………5分
②当p>0时，h(x)=px2－2x+p图象为开口向上抛物线，
称轴为x=∈（0，+∞）.
∴h(x)min=p－.
只需p－≥0，即p≥1时h(x)≥0，g′(x) ≥0，
∴g(x)在(0,+ ∞)单调递增，∴p≥1适合题意.…………………………7分
③当p<0时，h(x)=px2－2x+p图象为开口向下的抛物线，
其对称轴为x=（0，+∞），
只需h(0)≤0，即p≤0时h(0)≤（0,+ ∞)恒成立.
∴g′(x)<0 ，∴g(x)在（0,+ ∞）单调递减，
∴p<0适合题意.
综上①②③可得，p≥1或p≤0.……………………………………9分
（III）证明：①即证：lnx－x+1≤0 (x>0)，
设.
当x∈（0，1）时，k′(x)>0，∴k(x)为单调递增函数；
当x∈（1，∞）时，k′(x)<0，∴k(x)为单调递减函数；
∴x=1为k(x)的极大值点，
∴k(x)≤k(1)=0.
即lnx－x+1≤0，∴lnx≤x－1.………………………………11分
②由①知lnx≤x－1,又x>0，
∴结论成立.…………………………………………………………………………14分
5.已知数列的前n项和满足：（a为常数，且）．
（Ⅰ）求的通项公式；
（Ⅱ）设，若数列为等比数列，求a的值；
（Ⅲ）在满足条件（Ⅱ）的情形下，设，数列的前n项和为Tn，求证：．
解：（Ⅰ）∴
当时，
，即是等比数列． ∴； ………………4分
（Ⅱ）由（Ⅰ）知，，若为等比数列，
则有而
故，解得，再将代入得成立，
所以．
（III）证明：由（Ⅱ）知，所以
，
由得
所以，
从而
．
即． …………………………14分
6.已知数列满足
, ，．
（1）求证：是等比数列；
（2）求数列的通项公式；
（3）设，且对于恒成立，求的取值范
解：（1）由an＋1＝an＋6an－1，an＋1＋2an＝3(an＋2an－1) (n≥2)
∵a1＝5，a2＝5 ∴a2＋2a1＝15
故数列{an＋1＋2an}是以15为首项，3为公比的等比数列 …………5分
（2）由（1）得an＋1＋2an＝5·3n 由待定系数法可得(an＋1－3n＋1)＝－2(an－3n) 即an－3n＝2(－2)n－1 故an＝3n＋2(－2)n－1＝3n－(－2)n ………9分
（3）由3nbn＝n(3n－an)＝n[3n－3n＋(－2)n]＝n(－2)n，∴bn＝n(－)n
令Sn＝|b1|＋|b2|＋…＋|bn|＝＋2()2＋3()3＋…＋n()n
Sn＝()2＋2()3＋…＋(n－1)()n＋n()n＋1 …………11分
得Sn＝＋()2＋()3＋…＋()n－n()n+1＝－n()n+1＝2[1－()n]－n()n+1
∴ Sn＝6[1－()n]－3n()n+1＜6
要使得|b1|＋|b2|＋…＋|bn|＜m对于n∈N＊恒成立，只须m≥6 …14分
7.已知数列的首项（a是常数，且），（），数列的首项，（）。
（1）证明：从第2项起是以2为公比的等比数列；
（2）设为数列的前n项和，且是等比数列，求实数a的值；
（3）当a>0时，求数列的最小项。
解：（1）∵
∴
(n≥2) …………3分
由得，，
∵，∴ ，…………4分
即从第2项起是以2为公比的等比数列。…………5分
（2） …………8分
当n≥2时，
∵是等比数列, ∴(n≥2)是常数，
∴3a+4=0，即 。…………11分
（3）由（1）知当时，，
所以，…………13分
所以数列为2a+1，4a，8a-1，16a，32a+7，……
显然最小项是前三项中的一项。…………15分
当时，最小项为8a-1；
当时，最小项为4a或8a-1；………16分
当时，最小项为4a；
当时，最小项为4a或2a+1；…………17分
当时，最小项为2a+1。…………18分
8.已知函数f(x)=，设正项数列满足=l，．
(I)写出，的值;
(Ⅱ)试比较与的大小，并说明理由；
(Ⅲ)设数列满足=－，记Sn=．证明：当n≥2时,Sn＜(2n－1)．
解(1)，因为所以……………………………… 2分
（2）因为所以…………………………………3分
,……………………………………………5分
因为所以与同号，………………………………………………6分
因为，
…，即……………………………………………………………………8分
（3）当时，
，……………………………………………………………………10分
所以，……………………………………………12分
所以…………14分
9.已知，若数列{an}
成等差数列.
（1）求{an}的通项an;
（2）设 若{bn }的前n项和是Sn，且
解：设2，f(a1), f(a2), f(a3),……，f(an),2n+4的公差为d，则
2n+4=2+(n+2－1)dd=2,…………………………（2分）
……………………（4分）
（2），
10.（1）数列{an}和{bn}满足 （n=1，2，3…），求证{bn}为等差数列的充要条件是{an}为等差数列。（8分）
（2）数列{an}和{cn}满足，探究为等差数列的充分必要条件，需说明理由。[提示：设数列{bn}为
证明：（1）必要性 若{bn}为等差数列，设首项b1，公差d
则
∵ ∴{an}为是公差为的等差数列 ……4分
充分性 若{an}为等差数列，设首项a1，公差d
则
∴
当n=1时，b1=a1也适合
∵bn+1－bn=2d， ∴{bn}是公差为2d的等差数列 …………4分
（2）结论是：{an}为等差数列的充要条件是{cn}为等差数列且bn=bn+1
其中 （n=1，2，3…） …………4分
11.设集合W是满足下列两个条件的无穷数列{an}的集合：
① ②M是与n无关的常数.
（1）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈W
（2）设数列{bn}的通项为，求M的取值范围；
（3）设数列{cn}的各项均为正整数，且
（1）解：
设等差数列{an}的公差是d，则a1+2d=4，3a1+3d=18，
解得a1=8，d=－2，
所以……………………………………2分
由
=－1＜0
得适合条件①；
又
所以当n=4或5时，Sn取得最大值20，即Sn≤20，适合条件②
综上，{Sn}∈W………………………………………………4分
（2）解：
因为
所以当n≥3时，，此时数列{bn}单调递减；
当n=1，2时，，即b1＜b2＜b3，
因此数列{bn}中的最大项是b3=7
所以M≥7………………………………………………8分
（3）解：
假设存在正整数k，使得成立
由数列{cn}的各项均为正整数，可得
因为
由
因为
……………………
依次类推，可得
设
这显然与数列{cn}的各项均为正整数矛盾！
所以假设不成立，即对于任意n∈N*,都有成立.( 16分)
12.数列和数列（）由下列条件确定：
（1），；
（2）当时，与满足如下条件：当时，，；当时，，.
解答下列问题：
（Ⅰ）证明数列是等比数列；
（Ⅱ）记数列的前项和为，若已知当时，，求.
（Ⅲ）是满足的最大整数时，用，表示满足的条件.
解：（Ⅰ）当时，，
当时，，
所以不论哪种情况，都有，又显然，故数列是等比数列.…（4分）
（Ⅱ）由（Ⅰ）知，，故，
，所以
所以，，…（7分）
又当时，，故.（8分）
（Ⅲ）当时，，由（2）知不成立，故，从而对于，有，，于是，故，…………（10分）
若，则，
，所以，这与是满足的最大整数矛盾.
因此是满足的最小整数.（12分）
而，
因而，是满足的最小整数.（14分）
13.已知数列中，，．
（1）求；
（2）求数列的通项；
（3）设数列满足，求证：
解：（1）
（2）
—得
即：，
所以
所以
（3）由（2）得：，
所以是单调递增数列，故要证：只需证
若，则显然成立
若，则
所以
因此：
所以
所以
14. 已知数列满足，．
（Ⅰ）求数列的通项公式；
（Ⅱ）设，求数列的前项和；
（Ⅲ）设，数列的前项和为．求证：对任意的，．
解：（Ⅰ），，……………3分
又，数列是首项为，公比为的等比数列．……5分
， 即. ………………6分
（Ⅱ）．
． ………………9分
（Ⅲ），
． ……………………10分
当时，则
．
， 对任意的，． ………………………14分
15. 设数列满足 ，且数列是等差数列，数列是等比数列。
（I）求数列和的通项公式；
（II）是否存在，使，若存在，求出，若不存在，说明理由。
解（1）由已知，
公差 ………1分
………2分
＝ ………4分
由已知………5分
所以公比
………6分
………7分
（2）设
………8分
所以当时，是增函数。………10分
又，所以当时，………12分
又，………13分
所以不存在，使。………14分
16. 数列的首项，前n项和Sn与an之间满足
（1）求证：数列{}的通项公式；
（2）设存在正数k，使对一切
都成立，求k的最大值.
解：（1）证明：∵ …………（1分）
∴，∴，
∴ ………………（3分）
∴， ………………（5分）
数列为首项，以2为公差的等差数列。（6分）
（2）由（1）知
∴ ∴ …………（7分）
设，
则
…………（10分）
∴上递增，要使恒成立，只需
∵
∴ ………………（12分）
17.数列，
⑴是否存在常数、，使得数列是等比数列，若存在，求出、的值，若不存在，说明理由。
⑵设，证明：当时，.
解:设 ，
即 …………………………… (2分)
故 …………………………… (4分)
∴ ………(5分)
又 ……………………………………………………………………(6分)
故存在是等比数列 ……………(7分)
⑵证明：由⑴得 ∴，
故 ……………………………………………… (8分)
∵ ………………………… (9分)
∴
……………………………………（11分）
现证.
当，
故时不等式成立 ………………………………………………（12分）
当得
，且由，
∴ …………………………………… （14分）
18．已知数列满足.(1)求数列的通项公式；（2）设a>0,数列满足，若对成立，试求a的取值范围。
解：（1），又，
是公比为的等比数列，
（2），
现证：时，对成立。
① n=1时，成立;
② 假设n=k(k≥1)时，成立，则，
即n=k+1时，也成立，时，
a的取值范围是。
19.已知数列满足.(1)求数列的通项公式；（2）若数列的前n项和，，求证：。
解：（1），又，
是公比为的等比数列，
（2），
……①，②，①－②得：
，
20．设A（x1,y1）,B(x2,y2)是函数f(x)=的图象上任意两点，且
，已知点M的横坐标为.
（1） 求证：M点的纵坐标为定值；
（2） 若Sn=f(∈N*，且n≥2,求Sn;
（3） 已知an=，其中n∈N*.
Tn为数列{an}的前n项和，若Tn＜λ(Sn+1+1)对一切n∈N*都成立，试求λ的取值范围.
（1）证明：∵ ∴M是AB的中点.设M点的坐标为（x,y）,
由（x1+x2）=x=,得x1+x2=1，则x1=1-x2或x2=1-x1.
而y=(y1+y2)= ［f(x1)+f(x2)］ =(+log2
=(1+log2 =(1+log2
=(1+log2
∴M点的纵坐标为定值.
（2）由（1）知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f(
Sn=f(,
两式相加得：
2Sn=［f()+［f()+…+［f()
=
∴Sn=(n≥2,n∈N*).
(2)当n≥2时,an=
Tn=a1+a2+a3+…+an=［()
=(
由Tn＜λ(Sn+1+1)得＜λ·
∴λ＞
∵n+≥4,当且仅当n=2时等号成立,
∴
因此λ＞，即λ的取值范围是（+∞）
21．已知等差数列的首项为a，公差为b；等比数列的首项为b，公比为a，其中a，，且
（Ⅰ）求a的值；
（Ⅱ）若对于任意N*，总存在N*，使，求b的值；
（Ⅲ)甲说：一定存在使得对N*恒成立；乙说：一定存在使得对N*恒成立．你认为他们的说法是否正确？为什么？
解：（Ⅰ）∵ ，a，N*，
∴ ∴ ∴
∴ ∴ a＝2或a＝3．
∵当a＝3时，由得，即，与矛盾，故a＝3不合题意．
∴a＝3舍去， ∴a＝2．
（Ⅱ），，由可得．
∴．∴ 是5的约数，又，∴ b＝5 ．
(Ⅲ)若甲正确，则存在（）使，即对N*恒成立，
当时，，无解，所以甲所说不正确．
若乙正确，则存在（）使，即对N*恒成立，
当时，，只有在时成立，
而当时不成立，所以乙所说也不成立．
22.正项数列
（1）求；
（2）试确定一个正整数N，使当n>N时，不等式
成立；
（3）求证：
解：（1）
………………………………4分
（2）由
（3）将展开，
…………14分
23.,,…,是首项为1,公比为2的等比数列.对于满足0≤k≤20的整数k,数列,,…,由=确定.记C=.求：
⑴k=1时,C的值(保留幂的形式)；
⑵C最小时,k的值.
（注：=++…+）
简解：⑴可求得=(1≤n≤20),k=1时,=
C=+-.
⑵C=+=+=≥,当且仅当时,即=,k=10时,C最小.
24. 在数列中，
（Ⅰ）试比较与的大小；
（Ⅱ）证明：当时，.
解：（Ⅰ）由题设知，对任意，都有
，
………………………………6分
（Ⅱ）证法1：由已知得，
又.
当时，
…………………………………10分
设 ①
则 ②
①-②，得
……………………14分
证法2：由已知得，
（1） 当时，由，知不等式成立。………8分
（2） 假设当不等式成立，即，那么
要证 ，只需证
即证 ，则只需证………………10分
因为成立，所以成立.
这就是说，当时，不等式仍然成立.
根据（1）和（2），对任意，且，都有……14分
25．设无穷数列{an}具有以下性质：①a1=1；②当
（Ⅰ）请给出一个具有这种性质的无穷数列，使得不等式 对于任意的都成立，并对你给出的结果进行验证（或证明）；
（Ⅱ）若，其中，且记数列{bn}的前n项和Bn，证明：
解：（Ⅰ）令，
则无穷数列{an}可由a1 = 1，给出.
显然，该数列满足，且
…………6分
（Ⅱ）
……………………………………8分
又
26. 在个不同数的排列（即前面某数大于后面某数）则称构成一个逆序，一个排列的全部逆序的总数称为该排列的逆序数，例如排列（2，40，3，1）中有逆序“2与1”，“40与3”，“40与1”，“3与1”其逆序数等于4. 已知n+2个不同数的排列的逆序数是2.
（1）求（1，3，40，2）的逆序数；
（2）写出的逆序数an
（3）令.
解：（1） …………4分
（2）n+2个数中任取两个数比较大小，共有个大小关系
…………8分
（3）
…………14分
27．已知数列的前项和为，且对于任意的，恒有，设
．
（Ⅰ）求证：数列是等比数列；
（Ⅱ）求数列的通项公式和；
（Ⅲ）若，证明：．
解（1）（6分）当时，，得．
∵，∴当时，，
两式相减得：，∴．
∴，
∴是以为首项，2为公比的等比数列．
（2）（4分）由（1）得，∴．
∴．
（3）（6分），，
由为正项数列，所以也为正项数列，
从而，所以数列递减．
所以．
另证：由，
所以
．
28已知数列{an}满足a1=5，a2=5，an+1=an+6an－1（n≥2，n∈N*），若数列
是等比数列.
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：当k为奇数时，；
（Ⅲ）求证：
解（Ⅰ）∵为等比数列，
∴
应为常数， ∴
得=2或=－3 …………………………2分
当=2时，可得为首项是 ，公比为3的等比数列，
则 ①
当=－3时，为首项是，公比为－2的等比数列，
∴ ②
①－②得， ………………4分
（注：也可由①利用待定系数或同除2n+1得通项公式）
（Ⅱ）当k为奇数时，
∴ ……………………8分
（Ⅲ）由（Ⅱ）知k为奇数时， …………10分
①当n为偶数时，
②当n为奇数时，
= ………………12分
29.已知, 数列满足以下条件:
(1) 求数列的通项公式;
(2) 数列是有限数列时, 当时, 求点存在的范围;
(3) 数列是无限数列时, 当时, 将点存在的范围用图形表示出来.
解: (1) , , 则, .
, , 则, .
(2) 数列是有限数列时, 设项数为. 当时, , ,
. 点在线段上.
(3) 当时, ,
即, 由
得点存在的范围在如图阴影部分内.
30.设f1(x)=，定义fn+1 (x)= f1［fn(x)］，an =（n∈N*）.
(1) 求数列｛an｝的通项公式；
(2) 若，Qn=（n∈N*），试比较9T2n与
Qn的大小，并说明理由.
解：（1）∵f1(0)=2，a1==，fn+1(0)= f1［fn(0)］=,
∴an+1==== -= -an.
∴数列｛an｝是首项为,公比为-的等比数列，∴an=()n-1.
（2）∵T2 n = a1+2a 2+3a 3+…+(2n-1)a 2 n-1+2na 2 n，
∴T2 n= (-a1)+(-)2a 2+(-)3a 3+…+(-)(2n-1)a2 n－1+2na2 n
= a 2+2a 3+…+(2n－1)a2 n－na2 n.
两式相减，得T2 n= a1+a2+a 3+…+a2 n+na2 n.
∴T2n =+n×(-)2n-1=-(-)2n+(-)2n-1.
T2n =-(-)2n+(-)2n-1=(1-).
∴9T2n=1-.
又Qn=1-，
当n=1时，22 n= 4,(2n+1)2=9,∴9T2 n＜Q n；
当n=2时，22 n=16,(2n+1)2=25,∴9T2 n＜Qn；
当n≥3时，，
∴9T2 n＞Q n.
