至高考数学文科山东卷
2009年普通高等学校招生全国统一考试(山东卷)
文科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 集合,,若,则的值为( )
A.0 B.1 C.2 D.4
【解析】:∵,,∴∴,故选D.
答案:D
【命题立意】:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
2. 复数等于( )
A. B. C. D.
【解析】: ,故选C.
答案:C
【命题立意】:本题考查复数的除法运算,分子、分母需要同乘以分母的共轭复数,把分母变为实数,将除法转变为乘法进行运算.
3. 将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A. B. C. D.
【解析】:将函数的图象向左平移个单位,得到函数即的图象,再向上平移1个单位,所得图象的函数解析式为,故选A.
答案:A
【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
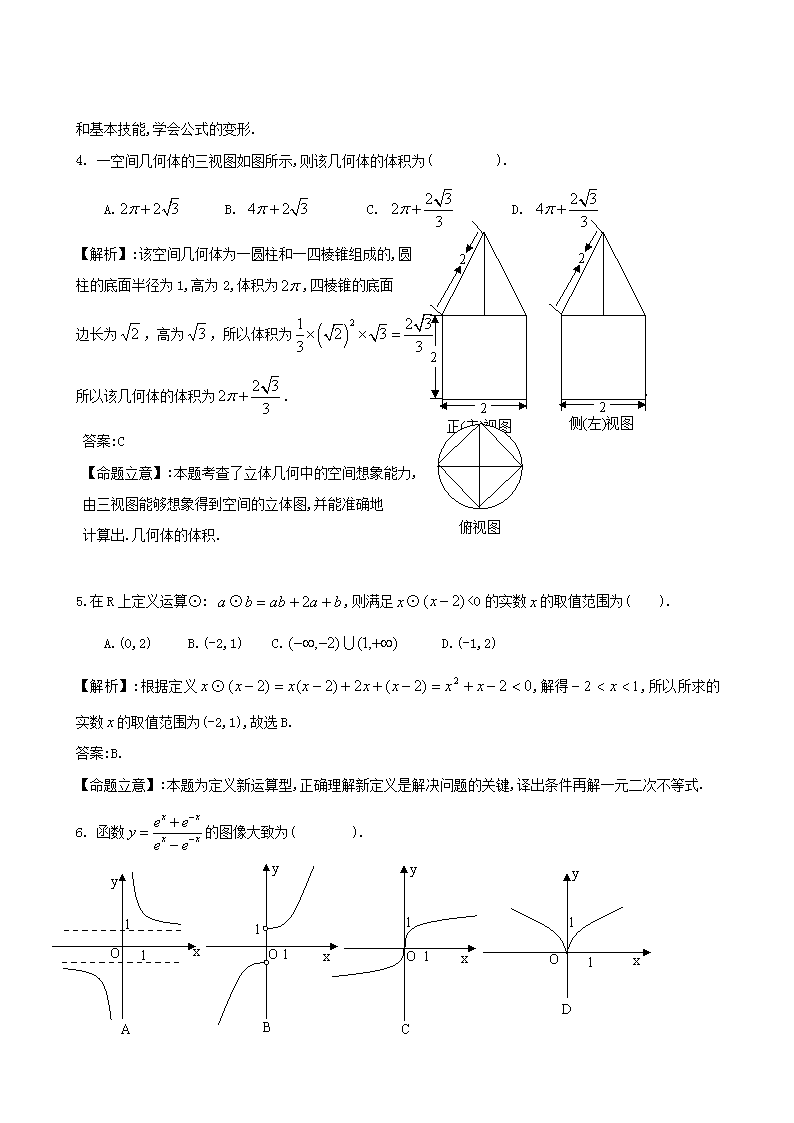
4. 一空间几何体的三视图如图所示,则该几何体的体积为( ).
2
2
侧(左)视图
2
2
2
正(主)视图
A. B. C. D.
【解析】:该空间几何体为一圆柱和一四棱锥组成的,俯视图
圆
柱的底面半径为1,高为2,体积为,四棱锥的底面
边长为,高为,所以体积为
所以该几何体的体积为.
答案:C
【命题立意】:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
5.在R上定义运算⊙: ⊙,则满足⊙<0的实数的取值范围为( ).
A.(0,2) B.(-2,1) C. D.(-1,2)
【解析】:根据定义⊙,解得,所以所求的实数的取值范围为(-2,1),故选B.
答案:B.
【命题立意】:本题为定义新运算型,正确理解新定义是解决问题的关键,译出条件再解一元二次不等式.
6. 函数的图像大致为( ).
1
x
y
1
O
A
x
y
O
1
1
B
x
y
O
1
1
C
x
y
1
1
D
O
【解析】:函数有意义,需使,其定义域为,排除C,D,又因为,所以当时函数为减函数,故选A
答案:A.
【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
7. 定义在R上的函数f(x)满足f(x)= ,则f(3)的值为( )
A.-1 B. -2 C.1 D. 2
【解析】:由已知得,,,
,,故选B.
答案:B
【命题立意】:本题考查对数函数的运算以及推理过程..
A
B
C
P
第8题图
8.设P是△ABC所在平面内的一点,,则( )
A. B. C. D.
【解析】:因为,所以点P为线段AC的中点,所以应该选C。
答案:C
【命题立意】:本题考查了向量的加法运算和平行四边形法则,可以借助图形解答。
9. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,,则,反过来则不一定.所以“”是“”的必要不充分条件
答案:B.
【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
10. 设斜率为2的直线过抛物线的焦点F,且和轴交于点A,若△
OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A. B. C. D.
【解析】: 抛物线的焦点F坐标为,则直线的方程为,它与轴的交点为A,所以△OAF的面积为,解得.所以抛物线方程为,故选B
答案:B.
【命题立意】:本题考查了抛物线的标准方程和焦点坐标以及直线的点斜式方程和三角形面积的计算.考查数形结合的数学思想,其中还隐含着分类讨论的思想,因参数的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
11.在区间上随机取一个数x,的值介于0到之间的概率为( ).
A. B. C. D.
【解析】:在区间 上随机取一个数x,即时,要使的值介于0到之间,需使或,区间长度为,由几何概型知的值介于0到之间的概率为.故选A
答案:A
【命题立意】:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值的范围,再由长度型几何概型求得.
12. 已知定义在R上的奇函数,满足,且在区间[0,2]上是增函数,则( ).
A. B.
C. D.
【解析】:因为满足,所以,所以函数是以8为周期的周期函数, 则,,,又因为在R上是奇函数, ,得,,而由得,又因为在区间[0,2]上是增函数,所以,所以,即,故选D.
-8 -6 -4 -2 0 2 4 6 8
y
x
f(x)=m (m>0)
答案:D.
【命题立意】:本题综合考查了函数的奇偶性、单调性、周期性等性质,运用化归的数学思想和数形结合的思想解答问题.
第Ⅱ卷
二、填空题:本大题共4小题,每小题4分,共16分。
13.在等差数列中,,则.
【解析】:设等差数列的公差为,则由已知得解得,所以
答案:13.
【命题立意】:本题考查等差数列的通项公式以及基本计算.
14.若函数f(x)=a-x-a(a>0且a1)有两个零点,则实数a的取值范围是 .
【解析】: 设函数且和函数,则函数f(x)=a-x-a(a>0且a1)有两个零点, 就是函数且与函数有两个交点,由图象可知当时两函数只有一个交点,不符合,当时,因为函数的图象过点(0,1),而直线所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
答案:
开始
S=0,T=0,n=0
T>S
S=S+5
n=n+2
T=T+n
输出T
结束
是
否
【命题立意】:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答.
15.执行右边的程序框图,输出的T= .
【解析】:按照程序框图依次执行为S=5,n=2,T=2;
S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30
答案:30
【命题立意】:本题主要考查了循环结构的程序框图,一般都可以
反复的进行运算直到满足条件结束,本题中涉及到三个变量,
注意每个变量的运行结果和执行情况.
16.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
【解析】:设甲种设备需要生产天, 乙种设备需要生产天, 该公司所需租赁费为元,则,甲、乙两种设备生产A,B两类产品的情况为下表所示:
产品
设备
A类产品
(件)(≥50)
B类产品
(件)(≥140)
租赁费
(元)
甲设备
5
10
200
乙设备
6
20
300
则满足的关系为即:,
作出不等式表示的平面区域,当对应的直线过两直线的交点(4,5)时,目标函数取得最低为2300元.
答案:2300
【命题立意】:本题是线性规划的实际应用问题,需要通过审题理解题意,找出各量之间的关系,最好是列成表格,找出线性约束条件,写出所研究的目标函数,通过数形结合解答问题
三、解答题:本大题共6小题,共74分。
17.(本小题满分12分)设函数f(x)=2在处取最小值.
(15) 求的值;
(16) 在ABC中,分别是角A,B,C的对边,已知,求角C.
解:
(1)
因为函数f(x)在处取最小值,
所以,
由诱导公式知,
因为,所以.
(2)由(1)知
因为,
且A为ABC的内角,所以.
又因为所以由正弦定理,得,
也就是,
因为,所以或.
当时,;
当时,.
综上所述,或
【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合.
18.(本小题满分12分)
E
A
B
C
F
E1
A1
B1
C1
D1
D
如图,在直四棱柱ABCD-ABCD中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA=2,
E、E分别是棱AD、AA的中点
(Ⅰ)设F是棱AB的中点,证明:直线EE//平面FCC;
(Ⅱ)证明:平面D1AC⊥平面BB1C1C.
(Ⅰ)证明:
在直四棱柱ABCD-ABCD中,取A1B1的中点F1,
E
A
B
C
F
E1
A1
B1
C1
D1
D
F1
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E分别是棱AD、AA的中点,所以EE1//A1D,
所以CF1//EE1,又因为平面FCC,平面FCC,
所以直线EE//平面FCC.
E
A
B
C
F
E1
A1
B1
C1
D1
D
(Ⅱ)连接AC,在直棱柱中,CC1⊥平面ABCD,AC平面ABCD,
所以CC1⊥AC,因为底面ABCD为等腰梯形,AB=4, BC=2,
F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,
,△ACF为等腰三角形,且
所以AC⊥BC, 又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C,而平面D1AC,
所以平面D1AC⊥平面BB1C1C.
【命题立意】: 本题主要考查直棱柱的概念、线面平行和线面垂直位置关系的判定.熟练掌握平行和垂直的判定定理.完成线线、线面位置关系的转化.
19. (本小题满分12分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值
(2)
用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(1) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解: (1).设该厂本月生产轿车为n辆,由题意得,,所以n=2000. z=2000-100-300-150-450-600=400
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.
(3)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.
【命题立意】:本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.
20.(本小题满分12分)
等比数列{}的前n项和为,已知对任意的,点,均在函数且均为常数)的图像上
(1)求r的值;
(11)当b=2时,记 求数列的前项和
解:因为对任意的,点,均在函数且均为常数)的图像上.所以得,
当时,,
当时,,
当n=2时,
又因为{}为等比数列, 所以,即
解得
(2)由(1)知,,,
所以
,
两式相减,得
所以
【命题立意】:本题主要考查了等比数列的定义,通项公式,以及已知求的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前项和.
21.(本小题满分12分)
已知函数,其中
一、 当满足什么条件时,取得极值?
二、 已知,且在区间上单调递增,试用表示出的取值范围.
解: (1)由已知得,令,得,
要取得极值,方程必须有解,
所以△,即, 此时方程的根为
,,
所以
当时,
x
(-∞,x1)
x 1
(x1,x2)
x2
(x2,+∞)
+
0
-
0
+
增函数
极大值
减函数
极小值
增函数
所以在x 1, x2处分别取得极大值和极小值.
当时,
x
(-∞,x2)
x 2
(x2,x1)
x1
(x1,+∞)
-
0
+
0
-
减函数
极小值
增函数
极大值
减函数
所以在x 1, x2处分别取得极大值和极小值.
综上,当满足时, 取得极值
(2)要使在区间上单调递增,需使在上恒成立.
即恒成立, 所以
设,,
令得或(舍去),
当时,,当时,单调增函数;
当时,单调减函数,
所以当时,取得最大,最大值为.
所以
当时,,此时在区间恒成立,所以在区间上单调递增,当时最大,最大值为,所以
综上,当时, ;当时,
【命题立意】:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
22. (本小题满分14分)
设,在平面直角坐标系中,已知向量,向量,,动点的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且(O为坐标原点),并求出该圆的方程;
(3)已知,设直线与圆C:(1
0)在区间[0,]上单调递增,在区间[,]上单调递减,则ω=( ).
A. B. C.2 D.3
7.(2011山东,文7)设变量x,y满足约束条件则目标函数z=2x+3y+1的最大值为( ).
A.11 B.10 C.9 D.8.5
8.(2011山东,文8)某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( ).
A.63.6万元 B.65.5万元
C.67.7万元 D.72.0万元
9.(2011山东,文9)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( ).
A.(0,2) B.[0,2]
C.(2,+∞) D.[2,+∞)
10.(2011山东,文10)函数y=-2sin x的图象大致是( ).
11.(2011山东,文11)右图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是( ).
A.3 B.2 C.1 D.0
12.(2011山东,文12)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若=λ(λ∈R),=μ(μ∈R),且+=2,则称A3,A4调和分割A1,A2.已知点C(c,0),D(d,0)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( ).
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C,D可能同时在线段AB上
D.C,D不可能同时在线段AB的延长线上
13.(2011山东,文13)某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生.为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,
应在丙专业抽取的学生人数为 .
14.(2011山东,文14)执行下图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是 .
15.(2011山东,文15)已知双曲线-=1(a>0,b>0)和椭圆+=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
16.(2011山东,文16)已知函数f(x)=logax+x-b(a>0,且a≠1),当23)千元.设该容器的建造费用为y千元.
(1)写出y关于r的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的r.
22.(2011山东,文22)在平面直角坐标系xOy中,已知椭圆C:+y2=1.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=-3于点D(-3,m).
(1)求m2+k2的最小值;
(2)若|OG|2=|OD|·|OE|,
①求证:直线l过定点;
②试问点B,G能否关于x轴对称?若能,求出此时△ABG的外接圆方程;若不能,请说明理由.
山东文科
1.A ∵M={x|(x+3)(x-2)<0}={x|-30)的图象可知,=.∴ω=.
7.B 由已知可得x,y所满足的可行域如图阴影部分所示:
令y=-x+,
要使z取得最大值,只须将直线l0:y=-x平移至经过A点,且联立得A(3,1),∴zmax=2×3+3×1+1=10.
8.B ∵=-=-9.4×=9.1,
∴回归方程为=9.4x+9.1.
令x=6,得=9.4×6+9.1=65.5(万元).
9.C 根据抛物线的定义可知|FM|=y0+2,又由圆与准线相交可得y0+2>4,即y0>2,故选C.
10.C 令f(x)=x-2sin x,x∈R,则可知f(-x)=-f(x),
∴f(x)是奇函数,故排除A;又f'(x)=-2cos x,
可知f'(x)有无穷多个零点,即f(x)有无穷多个极值点,
故排除B、D,选C.
11.A ①正确,如图一直三棱柱,其中四边形BCC1B1与四边形BAA1B1是全等的矩形,且面BCC1B1⊥面
BAA1B1,即满足要求.
②正确,如图一正四棱柱ABCD-A1B1C1D1,即满足要求.
③正确.横卧的圆柱即可.如图.
12.D ∵C、D调和分割点A,B,∴=λ,=μ,且+=2,又A(0,0),B(1,0),C(c,0),D(d,0),其中c,d∈R,
∴(c,0)=(λ,0),(d,0)=(μ,0).
∴c=λ,d=μ.∴+=2.(*)
对A,若C为AB的中点,则=,即c=,将其代入(*)式,得=0,这是无意义的,故A错误;
对B,若D为AB的中点,同理得μ=d=,同样使(*)式无意义.故B错误.
对C,要使C、D同时在线段AB上,则0<λ<1,且0<μ<1,
∴>1,>1.∴+>2,这与+=2矛盾;
故C错误;显然D正确.
13.16 由分层抽样定义可知,应抽丙专业的人数为40×=40×=16(人).
14.68 由程序框图可知,y的变化情况为y=70×2+21×3+15×5=278,
进入循环,显然278>105,因此y=278-105=173;
此时173>105,故y=173-105=68.
经判断68>105不成立,输出此时y的值68.
15.-=1 由题意知a2+b2=16-9,即a2+b2=7,①
又=2×,即=,②
由①②得a2=4,b2=3.
∴双曲线方程为-=1.
16.2 ∵a>2,∴f(x)=logax+x-b在(0,+∞)上为增函数,且f(2)=loga2+2-b,f(3)=loga3+3-b,
∵20.
又∵f(x)在(0,+∞)上是单调函数,∴f(x)在(2,3)必存在唯一零点.
17.解:(1)由正弦定理,设===k,
则==.
所以=,
即(cos A-2cos C)sin B=(2sin C-sin A)cos B.
化简可得sin(A+B)=2sin(B+C).
又A+B+C=π.
所以sin C=2sin A.因此=2.
(2)由=2得c=2a.
由余弦定理及cos B=得
b2=a2+c2-2accos B=a2+4a2-4a2×=4a2.
所以b=2a.
又a+b+c=5,从而a=1,因此b=2.
18.解:(1)甲校两男教师分别用A、B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E、F表示.
从甲校和乙校报名的教师中各任选1名的所有可能的结果为:
(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种.
从中选出两名教师性别相同的结果有:(A,D),(B,D),(C,E),(C,F)共4种.
选出的两名教师性别相同的概率为P=.
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.
从中选出两名教师来自同一学校的结果有:
(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种.
选出的两名教师来自同一学校的概率为P==.
19.证明:(1)证法一:因为D1D⊥平面ABCD,且BD⊂平面ABCD,
所以D1D⊥BD.
又因为AB=2AD,∠BAD=60°,
在△ABD中,由余弦定理得BD2=AD2+AB2-2AD·ABcos 60°=3AD2,
所以AD2+BD2=AB2.因此AD⊥BD.
又AD∩D1D=D,所以BD⊥平面ADD1A1.
又AA1⊂平面ADD1A1,故AA1⊥BD.
证法二:因为D1D⊥平面ABCD,且BD⊂平面ABCD.
所以BD⊥D1D.
取AB的中点G,连接DG,
在△ABD中,由AB=2AD得AG=AD.
又∠BAD=60°,所以△ADG为等边三角形,
因此GD=GB.
故∠DBG=∠GDB,又∠AGD=60°,所以∠GDB=30°.
故∠ADB=∠ADG+∠GDB=60°+30°=90°.
所以BD⊥AD.
又AD∩D1D=D,所以BD⊥平面ADD1A1.
又AA1⊂平面ADD1A1,故AA1⊥BD.
(2)连接AC,A1C1.
设AC∩BD=E,连接EA1.
因为四边形ABCD为平行四边形,所以EC=AC.
由棱台定义及AB=2AD=2A1B1知A1C1∥EC且A1C1=EC.
所以四边形A1ECC1为平行四边形.
因此CC1∥EA1.
又因为EA1⊂平面A1BD,CC1⊄平面A1BD.
所以CC1∥平面A1BD.
20.解:(1)当a1=3时,不合题意;
当a1=2时,当且仅当a2=6,a3=18时,符合题意;
当a1=10时,不合题意.
因此a1=2,a2=6,a3=18,所以公比q=3.
故an=2·3n-1.
(2)因为bn=an+(-1)nln an
=2·3n-1+(-1)nln(2·3n-1)
=2·3n-1+(-1)n[ln 2+(n-1)ln 3]
=2·3n-1+(-1)n(ln 2-ln 3)+(-1)nnln 3.
所以S2n=b1+b2+…+b2n
=2(1+3+…+32n-1)+[-1+1-1+…+(-1)2n](ln 2-ln 3)+[-1+2-3+…+(-1)2n2n]ln 3
=2×+nln 3
=32n+nln 3-1.
21.解:(1)设容器的容积为V.
由题意知V=πr2l+πr3.
又V=,故l==-r=(-r).
由于l≥2r,因此03,所以c-2>0.
当r3-=0时,r=.
令=m,则m>0.
所以y'=(r-m)(r2+rm+m2).
①当0时,
当r=m时,y'=0;
当r∈(0,m)时,y'<0;
当r∈(m,2)时,y'>0.
所以r=m是函数y的极小值点,也是最小值点.
②当m≥2即3时,建造费用最小时r=.
22.(1)解:设直线l的方程为y=kx+t(k>0),
由题意,t>0.
由方程组得(3k2+1)x2+6ktx+3t2-3=0.
由题意Δ>0,所以3k2+1>t2.
设A(x1,y1),B(x2,y2),
由韦达定得理x1+x2=-.
所以y1+y2=.
由于E为线段AB的中点,
因此xE=-,yE=,
此时kOE==-.
所以OE所在直线方程为y=-x.
又由题设知D(-3,m),令x=-3,得m=,即mk=1.
所以m2+k2≥2mk=2.
当且仅当m=k=1时上式等号成立.
此时由Δ>0得00,
解得G(-,),
又E(-,),D(-3,),
由距离公式及t>0得
|OG|2=(-)2+()2=,
|OD|==,
|OE|=
=,
由|OG|2=|OD|·|OE|得t=k,
因此直线l的方程为y=k(x+1),
所以直线l恒过定点(-1,0).
2012年普通高等学校招生全国统一考试(山东卷)
文科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)若复数z满足为虚数单位),则为
(A)3+5i (B)3-5i (C)-3+5i (D)-3-5i
(2)已知全集,集合,,则为
(A){1,2,4} (B){2,3,4} (C){0,2,4} (D){0,2,3,4}
(3)函数的定义域为
(A) (B) (C) (D)
(4)在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
(A)众数 (B)平均数 (C)中位数 (D)标准差
(5)设命题p:函数的最小正周期为;命题q:函数的图象关于直线
对称.则下列判断正确的是
(A)p为真 (B)为假 (C)为假 (D)为真
(6)设变量满足约束条件则目标函数的取值范围是
(A) (B) (C) (D)
(7)执行右面的程序框图,如果输入=4,那么输出的n的值为
(A)2 (B)3 (C)4 (D)5
(8)函数的最大值与最小值之和为
(A) (B)0 (C)-1 (D)
(9)圆与圆的位置关系为
(A)内切 (B)相交 (C)外切 (D)相离
(10)函数的图象大致为
(11)已知双曲线:的离心率为2.若抛物线的焦点到双曲线的渐近线的距离为2,则抛物线的方程为
(A) (B) (C) (D)
(12)设函数,.若的图象与的图象有且仅有两个不同的公共点,则下列判断正确的是
(A) (B)
(C) (D)
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
(13)如图,正方体的棱长为1,E为线段上的一点,则三棱锥的体积为_____.
(14)右图是根据部分城市某年6月份的平均气温(单位:℃
)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为,,,,,.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
(15)若函数在[-1,2]上的最大值为4,最小值为m,且函数在上是增函数,则a=____.
(16)如图,在平面直角坐标系中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,的坐标为____.
三、解答题:本大题共6小题,共74分.
(17)(本小题满分12分)
在△ABC中,内角所对的边分别为,已知.
(Ⅰ)求证:成等比数列;
(Ⅱ)若,求△的面积S.
(18)(本小题满分12分)
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
(19) (本小题满分12分)
如图,几何体是四棱锥,△为正三角形,.
(Ⅰ)求证:;
(Ⅱ)若∠,M为线段AE的中点,
求证:∥平面.
(20) (本小题满分12分)
已知等差数列的前5项和为105,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)对任意,将数列中不大于的项的个数记为.求数列的前m项和.
(21) (本小题满分13分)
如图,椭圆的离心率为,直线和所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线与椭圆M有两个不同的交点与矩形ABCD有两个不同的交点.求的最大值及取得最大值时m的值.
(22) (本小题满分13分)
已知函数为常数,e=2.71828…是自然对数的底数),曲线在点处的切线与x轴平行.
(Ⅰ)求k的值;
(Ⅱ)求的单调区间;
(Ⅲ)设,其中为的导函数.证明:对任意.
参考答案:
一、选择题:
(1)A (2)C (3)B (4)D (5)C (6)A (7)B (8)A (9)B (10)D (11)D (12)B
(12)解:设,则方程与同解,故其有且仅有两个不同零点.由得或.这样,必须且只须或,因为,故必有由此得.不妨设,则.所以,比较系数得,故.,由此知,故答案为B.
二、填空题
(13) 以△为底面,则易知三棱锥的高为1,故.
(14)9 最左边两个矩形面积之和为0.10×1+0.12×1=0.22,总城市数为11÷0.22=50,最右面矩形面积为0.18×1=0.18,50×0.18=9.
(15) 当时,有,此时,此时为减函数,不合题意.若,则,故,检验知符合题意.
(16)
三、解答题
(17)(I)由已知得:
,
,
,
再由正弦定理可得:,
所以成等比数列.
(II)若,则,
∴,
,
∴△的面积.
(18)(I)从五张卡片中任取两张的所有可能情况有如下10种:红1红2,红1红3,红1蓝1,红1蓝2,红2红
3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.其中两张卡片的颜色不同且标号之和小于4的有3种情况,故所求的概率为.
(II)加入一张标号为0的绿色卡片后,从六张卡片中任取两张,除上面的10种情况外,多出5种情况:红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,即共有15种情况,其中颜色不同且标号之和小于4的有8种情况,所以概率为.
(19)(I)设中点为O,连接OC,OE,则由知,,
又已知,所以平面OCE.
所以,即OE是BD的垂直平分线,
所以.
(II)取AB中点N,连接,
∵M是AE的中点,∴∥,
∵△是等边三角形,∴.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即,
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
(20)(I)由已知得:
解得,
所以通项公式为.
(II)由,得,
即.
∵,
∴是公比为49的等比数列,
∴.
(21)(I)……①
矩形ABCD面积为8,即……②
由①②解得:,
∴椭圆M的标准方程是.
(II),
设,则,
由得.
.
当过点时,,当过点时,.
①当时,有,
,
其中,由此知当,即时,取得最大值.
②由对称性,可知若,则当时,取得最大值.
③当时,,,
由此知,当时,取得最大值.
综上可知,当和0时,取得最大值.
(22)(I),
由已知,,∴.
(II)由(I)知,.
设,则,即在上是减函数,
由知,当时,从而,
当时,从而.
综上可知,的单调递增区间是,单调递减区间是.
(III)由(II)可知,当时,≤0<1+,故只需证明在时成立.
当时,>1,且,∴.
设,,则,
当时,,当时,,
所以当时,取得最大值.
所以.
综上,对任意,.