2014年版高考物理专题目一第2讲牛顿运动定律二轮强化训练

2014年版高考物理专题目一第2讲牛顿运动定律二轮强化训练

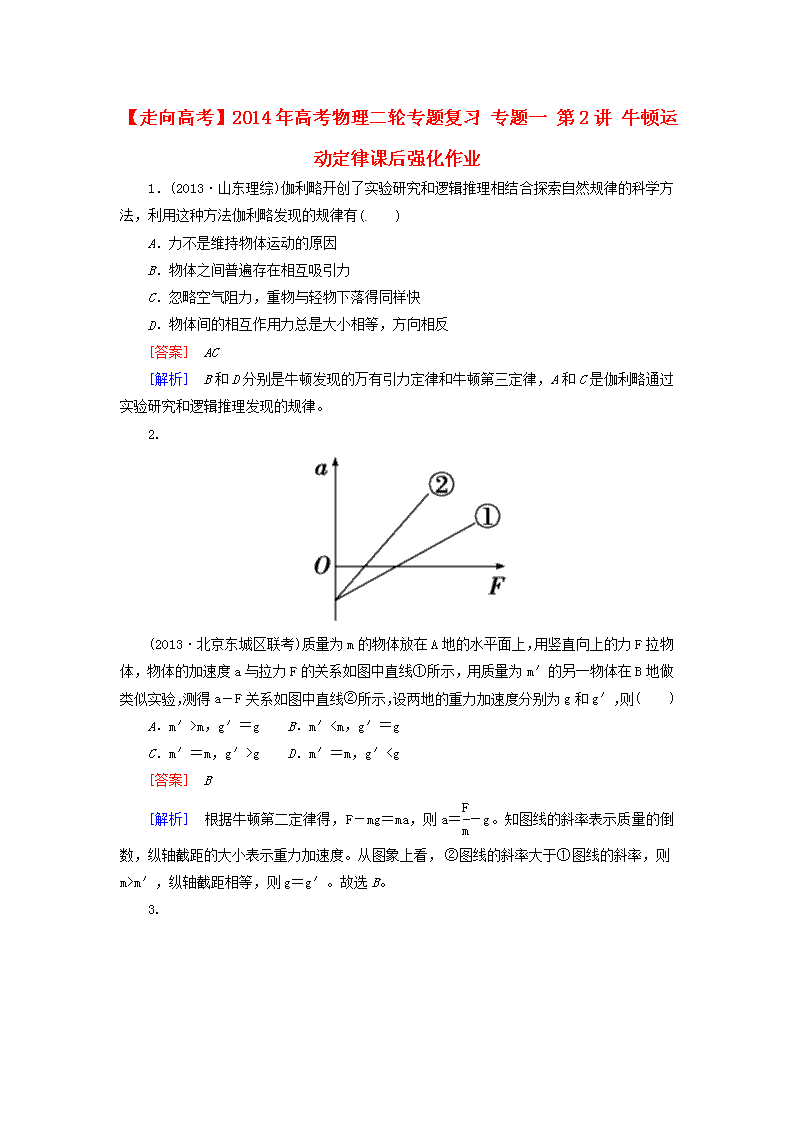
‎【走向高考】2014年高考物理二轮专题复习 专题一 第2讲 牛顿运动定律课后强化作业 ‎1．(2013·山东理综)伽利略开创了实验研究和逻辑推理相结合探索自然规律的科学方法，利用这种方法伽利略发现的规律有(　　)‎ A．力不是维持物体运动的原因 B．物体之间普遍存在相互吸引力 C．忽略空气阻力，重物与轻物下落得同样快 D．物体间的相互作用力总是大小相等，方向相反 ‎[答案]　AC ‎[解析]　B和D分别是牛顿发现的万有引力定律和牛顿第三定律，A和C是伽利略通过实验研究和逻辑推理发现的规律。‎ ‎2.‎ ‎(2013·北京东城区联考)质量为m的物体放在A地的水平面上，用竖直向上的力F拉物体，物体的加速度a与拉力F的关系如图中直线①所示，用质量为m′的另一物体在B地做类似实验，测得a－F关系如图中直线②所示，设两地的重力加速度分别为g和g′，则(　　)‎ A．m′>m，g′＝g B．m′g D．m′＝m，g′m′，纵轴截距相等，则g＝g′。故选B。‎ ‎3.‎ ‎(2013·江苏涟水期末)如图所示，小车上固定一弯折硬杆ABC，C端固定一质量为m的小球。已知α角恒定，当小车水平向左做变加速直线运动时，BC杆对小球的作用力的方向(　　)‎ A．一定沿着杆向上 B．一定竖直向上 C．可能水平向左 D．随加速度a的数值的改变而改变 ‎[答案]　D ‎[解析]　BC杆对小球的作用力有两个效果，竖直方向与重力平衡，竖直方向分力不变，水平方向提供产生加速度的合外力，大小随加速度变化而变化，所以BC杆对小球的作用力随加速度a的数值的改变而改变，D正确，A、B、C错误。‎ ‎4．(2013·黑龙江牡丹江地区六市县第一次联考)一个物体在多个力的作用下处于静止状态。若仅使其中的一个力保持方向不变、大小均匀减小到零，然后又从零均匀恢复到原来的大小，在这过程中其余各力均不变，则能正确描述该过程中物体速度和加速度随时间变化情况的是(　　)‎ ‎[答案]　BC ‎[解析]　当一个力方向保持不变、大小均匀减小到零时，物体的加速度沿该力的反方向均匀增大，当该力又从零均匀恢复到原来的大小时，物体的加速度沿该力的反方向再均匀减小到零，故C正确，D错误；在v－t图象中，曲线上一点的切线的斜率表示加速度，根据加速度先增大后减小且方向不变的特点可知，B正确，A错误。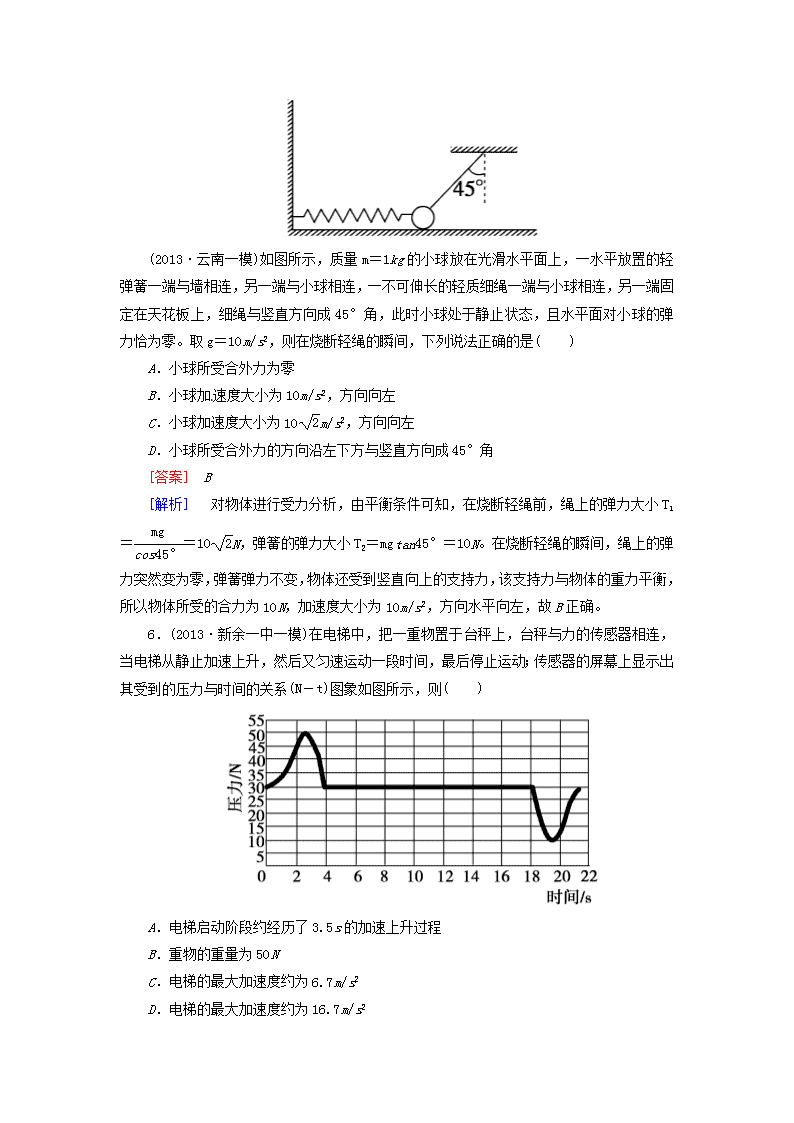‎ ‎5.‎ ‎(2013·云南一模)如图所示，质量m＝‎1kg的小球放在光滑水平面上，一水平放置的轻弹簧一端与墙相连，另一端与小球相连，一不可伸长的轻质细绳一端与小球相连，另一端固定在天花板上，细绳与竖直方向成45°角，此时小球处于静止状态，且水平面对小球的弹力恰为零。取g＝‎10m/s2，则在烧断轻绳的瞬间，下列说法正确的是(　　)‎ A．小球所受合外力为零 B．小球加速度大小为‎10m/s2，方向向左 C．小球加速度大小为‎10‎m/s2，方向向左 D．小球所受合外力的方向沿左下方与竖直方向成45°角 ‎[答案]　B ‎[解析]　 对物体进行受力分析，由平衡条件可知，在烧断轻绳前，绳上的弹力大小T1＝＝10N，弹簧的弹力大小T2＝mgtan45°＝10N。在烧断轻绳的瞬间，绳上的弹力突然变为零，弹簧弹力不变，物体还受到竖直向上的支持力，该支持力与物体的重力平衡，所以物体所受的合力为10N，加速度大小为‎10m/s2，方向水平向左，故B正确。‎ ‎6．(2013·新余一中一模)在电梯中，把一重物置于台秤上，台秤与力的传感器相连，当电梯从静止加速上升，然后又匀速运动一段时间，最后停止运动；传感器的屏幕上显示出其受到的压力与时间的关系(N－t)图象如图所示，则(　　)‎ A．电梯启动阶段约经历了3.5s的加速上升过程 B．重物的重量为50N C．电梯的最大加速度约为‎6.7m/s2‎ D．电梯的最大加速度约为‎16.7m/s2‎ ‎[答案]　C ‎[解析]　由图象可知：在0～4s内，物体受到的支持力大于重力，物体处于加速上升过程，A错误；在匀速运动阶段，重力大小等于支持力，为30N，B错误；电梯的最大加速度a＝m/s2≈‎6.7m/s2(或a＝m/s2≈－‎6.7m/s2)，C正确，D错误。‎ ‎7．(2013·广东理综)‎ 游乐场中，从高处A到水面B处有两条长度相同的光滑轨道，甲、乙两小孩沿不同轨道同时从A处自由滑向B处，下列说法正确的是(　　)‎ A．甲的切向加速度始终比乙的大 B．甲、乙在同一高度的速度大小相等 C．甲、乙在同一时刻总能到达同一高度 D．甲比乙先到达B处 ‎[答案]　BD ‎[解析]　‎ 切向加速度a＝gsinθ，开始甲大于乙后来甲小于乙，选项A错误；由机械能守恒可知。甲、乙在同一高度的速度大小相等，选项B正确；画出甲、乙的速率图象如图所示，由于两种情况路程相同(即图象与t轴所围的图形的面积相同)，最后的速率相同，由图可知甲比乙先到达B处，同一时刻，甲的位置总低于乙，选项C错、D对。‎ ‎8．(2013·南昌模拟)‎ 在光滑水平面上，a、b两小球沿水平面相向运动。当小球间距小于或等于L时，受到大小相等、方向相反的相互排斥恒力作用，当小球间距大于L时，相互间的排斥力为零。两小球在相互作用区间运动时始终未接触。两小球运动时速度v随时间t的变化关系图象如图所示，由图可知(　　)‎ A．a球质量大于b球质量 B．在t1时刻两小球间距最小 C．在0～t2时间内两小球间距逐渐减小 D．在0～t3时间内b球所受排斥力的方向始终与运动方向相反 ‎[答案]　AC ‎[解析]　由图象可知，在两球相互作用的过程中，a球的加速度小于b球的加速度，因此a球质量大于b球质量，选项A正确；在t2时刻两球速度相同，此时距离最小，0～t2时间内两小球间距逐渐减小，因此选项B错误，选项C正确；由两球受力运动分析可知，b球所受排斥力的方向在0～t1时间内与运动方向相反，在t1～t3时间内与运动方向相同，因此选项D错误，所以答案选AC。‎ ‎9．(2013·吉林实验中学二模)如图甲所示，A、B两物体叠放在光滑水平面上，对物体B施加一水平变力F，F－t关系如图乙所示，两物体在变力F作用下由静止开始运动且始终保持相对静止，则(　　)‎ A．t0时刻，两物体之间的摩擦力最大 B．t0时刻，两物体之间的速度方向开始改变 C．t0～2t0时间内，两物体之间的摩擦力逐渐增大 D．t0～2t0时间内，物体A所受的摩擦力方向始终与变力F的方向相同 ‎[答案]　CD ‎[解析]　 两物体始终保持相对静止，故t0时刻，两物体的加速度为零，两物体之间无摩擦力，A错误；0～t0时刻两物体做加速度减小的加速运动，t0时刻速度达到最大，t0～2t0时间内两物体做加速度增大的减速运动，到2t0时刻速度减到零，故0～t0两物体的速度方向没有改变，B错误；0～t0时刻物体A所受的摩擦力方向始终与变力F的方向相同，D正确；两物体之间的摩擦力f＝mAa＝，f随F的变化而变化，故C正确。‎ ‎10.‎ ‎(2013·江苏六市调研)如图所示，质量为m1的木块和质量为m2的长木板叠放在水平地面上。现对木块施加一水平向右的拉力F。木块在长木板上滑行，而长木板保持静止状态。已知木块与长木板间的动摩擦因数为μ1，长木板与地面间的动摩擦因数为μ2，且最大静摩擦力与滑动摩擦力相等，则(　　)‎ A．μ1>μ2‎ B．μ1<μ2‎ C．若改变F的大小，当F>μ1(m1＋m2)g时，长木板将开始运动 D．若将F作用于长木板，当F>(μ1＋μ2)(m1＋m2)g时，长木板与木块将开始相对滑动 ‎[答案]　D ‎[解析]　以m2为研究对象，水平方向受到m1施加的向右的滑动摩擦力μ‎1m1g和地面施加的水平向左的静摩擦力f2，根据平衡条件得f2＝μ‎1m1g，由于最大静摩擦力与滑动摩擦力相等，故μ2(m1＋m2)g≥f2＝μ‎1m1g，根据上式，不能判断μ1与μ2的大小关系，A、B错误；若改变F的大小，当F>μ2(m1＋m2)g时，长木板将开始运动，C错误；若将F作用于长木板，设长木板与木块刚好开始相对滑动的加速度为a，以m1为研究对象，则a＝μ‎1g，此时对于m2有F－μ‎1m1g－μ2(m1＋m2)g＝m2μ‎1g，F＝(μ1＋μ2)(m1＋m2)g，故D正确。‎ ‎11.‎ ‎(2013·山东济南一模)如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k，C为一固定挡板，系统处于静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度和从开始到此时物块A的位移。(重力加速度为g)‎ ‎[答案]　， ‎[解析]　令x1表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知 mAgsinθ＝kx1①‎ 令x2表示B刚要离开C时弹簧的伸长量，a表示此时A的加速度，由胡克定律和牛顿定律可知：‎ kx2＝mBgsinθ②‎ F－mAgsinθ－kx2＝mAa③‎ 由②③式可得a＝④‎ 由题意d＝x1＋x2⑤‎ 由①②⑤式可得d＝ ‎12.‎ ‎(2013·上海嘉定区检测)滑雪运动中，滑雪板与雪地之间的相互作用与滑动速度有关，当滑雪者的速度超过‎4m/s时，滑雪板与雪地间的动摩擦因数就会由μ1＝0.25变为μ2＝0.125。一滑雪者从倾角θ＝37°的坡顶A处由静止开始自由下滑，滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地，最后停在C处，如图所示，不计空气阻力，坡长L＝‎26m，取g＝‎10m/s2，sin37°＝0.6，cos37°＝0.8，求：‎ ‎(1)滑雪者从静止开始到动摩擦因数发生变化所经历的时间；‎ ‎(2)滑雪者到达B处的速度；‎ ‎(3)在图中画出滑雪者速度大小为‎10m/s时的受力示意图，并求出此时的加速度的大小。‎ ‎[答案]　(1)1s　(2)‎16m/s　(3)AB段加速度大小为‎5‎m/s2，BC段加速度大小为‎1.25m/s2‎ ‎[解析]　(1)在AB段速度小于‎4m/s时，a1＝gsin37°－μ1gcos37°＝10×‎0.6m/s2－0.25×10×‎0.8m/s2＝‎4m/s2‎ 则t1＝＝s＝1s ‎(2)s1＝a1t＝×4×‎12m＝‎‎2m 速度大于‎4m/s时：a2＝gsin37°－μ2gcos37°＝10×‎0.6m/s2－0.125×10×‎0.8m/s2＝‎5m/s2‎ s2＝L－s1＝‎26m－‎2m＝‎‎24m vB＝＝m/s＝‎16m/s ‎(3)受力分析如图 当速度等于‎10m/s时动摩擦因数为0.125，分别在AB段与BC段两处，在AB段时加速度为a2＝gsin37°－μ2gcos37°＝10×‎0.6m/s2－0.125×10×‎0.8m/s2＝‎5m/s2‎ 在BC段时加速度为a3＝－μ‎2g＝－0.125×‎10m/s2＝－‎1.25m/s2‎ ‎13．(2013·江苏单科)‎ 如图所示，将小砝码置于桌面上的薄纸板上，用水平向右的拉力将纸板迅速抽出，砝码的移动很小，几乎观察不到，这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为m1和m2，各接触面间的动摩擦因数均为μ。重力加速度为g。‎ ‎(1)当纸板相对砝码运动时，求纸板所受摩擦力的大小；‎ ‎(2)要使纸板相对砝码运动时，求所需拉力的大小；‎ ‎(3)本实验中，m1＝‎0.5kg，m2＝‎0.1kg，μ＝0.2，砝码与纸板左端的距离d＝‎0.1m，取g＝‎10m/s2。若砝码移动的距离超过l＝‎0.002m，人眼就能感知。为确保实验成功，纸板所需的拉力至少多大？‎ ‎[答案]　(1)μ(‎2m1＋m2)g　(2)F>2μ(m1＋m2)g　(3)22.4N ‎[解析]　(1)砝码对纸板的摩擦力f1＝μm‎1g 桌面对纸板的摩擦力f2＝μ(m1＋m2)g f＝f1＋f2‎ 解得f＝μ(‎2m1＋m2)g ‎(2)设砝码的加速度为a1，纸板的加速度为a2，则 f1＝m‎1a1　‎F－f1－f2＝m‎2a2‎ 发生相对运动a2>a1‎ 解得F>2μ(m1＋m2)g ‎(3)纸板抽出前，砝码运动的距离x1＝a1t 纸板运动的距离d＋x1＝a2t 纸板抽出后，砝码在桌面上运动的距离：x2＝a3t　‎ l＝x1＋x2‎ 由题意知a1＝a3，a1t1＝a3t2‎ 解得F＝2μg 代入数据得F＝22.4N