北京市高考数学试卷理科解析

北京市高考数学试卷理科解析

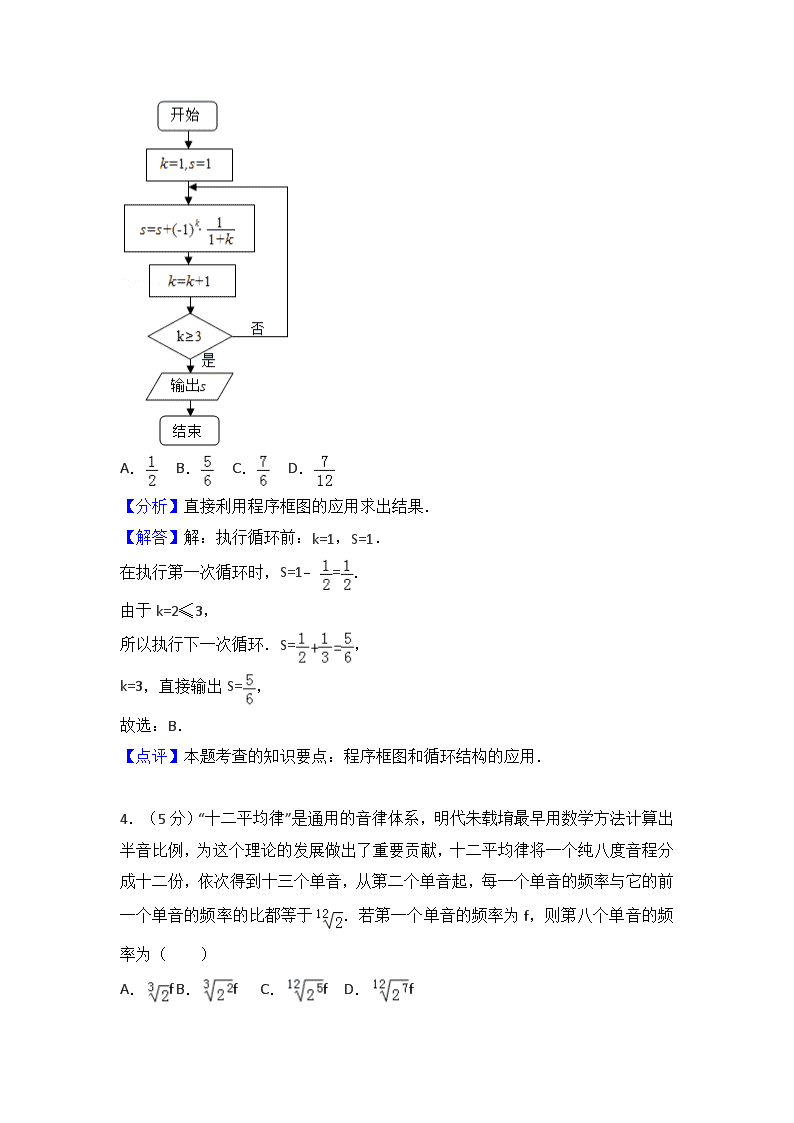
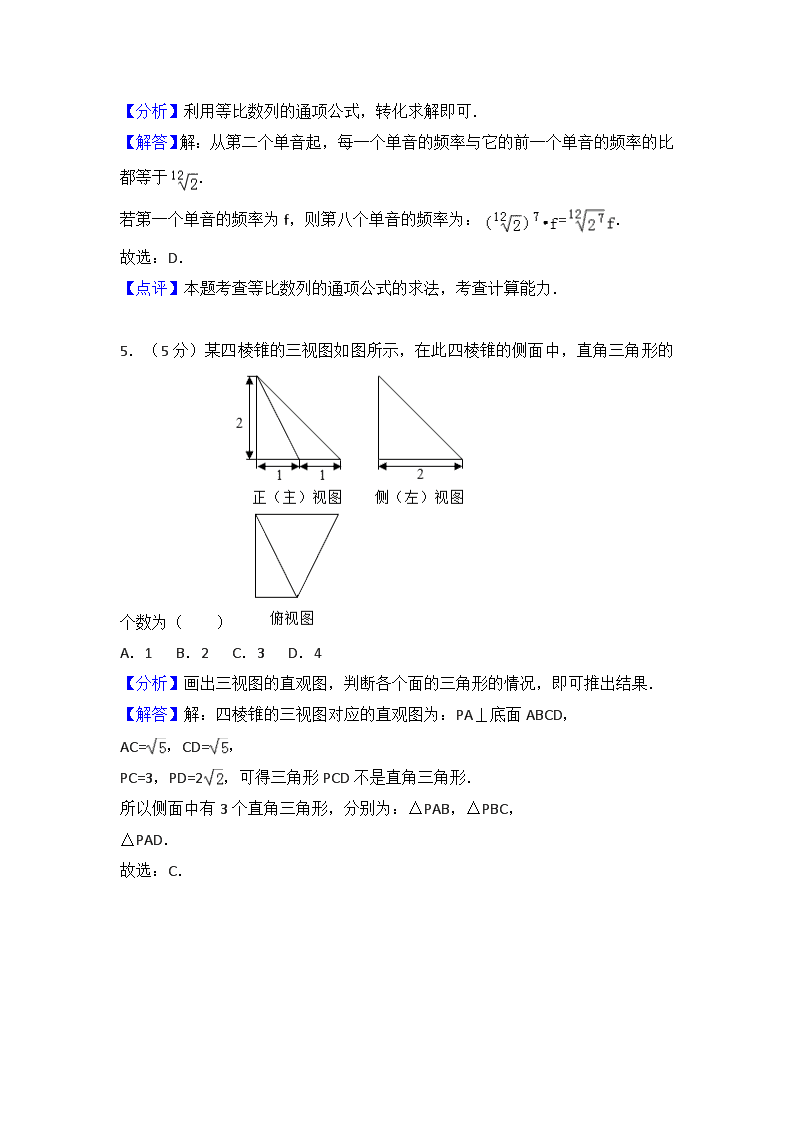
‎2018年北京市高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎1．（5分）已知集合A={x||x|＜2}，B={﹣2，0，1，2}，则A∩B=（　　）‎ A．{0，1} B．{﹣1，0，1} C．{﹣2，0，1，2} D．{﹣1，0，1，2}‎ ‎【分析】根据集合的基本运算进行计算即可．‎ ‎【解答】解：A={x||x|＜2}={x|﹣2＜x＜2}，B={﹣2，0，1，2}，‎ 则A∩B={0，1}，‎ 故选：A．‎ ‎【点评】本题主要考查集合的基本运算，根据集合交集的定义是解决本题的关键．比较基础．‎ ‎　‎ ‎2．（5分）在复平面内，复数的共轭复数对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【分析】利用复数的除法运算法则，化简求解即可．‎ ‎【解答】解：复数==，‎ 共轭复数对应点的坐标（，﹣）在第四象限．‎ 故选：D．‎ ‎【点评】本题考查复数的代数形式的乘除运算，复数的几何意义，是基本知识的考查．‎ ‎　‎ ‎3．（5分）执行如图所示的程序框图，输出的s值为（　　）‎ A． B． C． D．‎ ‎【分析】直接利用程序框图的应用求出结果．‎ ‎【解答】解：执行循环前：k=1，S=1．‎ 在执行第一次循环时，S=1﹣=．‎ 由于k=2≤3，‎ 所以执行下一次循环．S=，‎ k=3，直接输出S=，‎ 故选：B．‎ ‎【点评】本题考查的知识要点：程序框图和循环结构的应用．‎ ‎　‎ ‎4．（5分）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f，则第八个单音的频率为（　　）‎ A．f B．f C．f D．f ‎【分析】利用等比数列的通项公式，转化求解即可．‎ ‎【解答】解：从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．‎ 若第一个单音的频率为f，则第八个单音的频率为：=．‎ 故选：D．‎ ‎【点评】本题考查等比数列的通项公式的求法，考查计算能力．‎ ‎　‎ ‎5．（5分）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【分析】画出三视图的直观图，判断各个面的三角形的情况，即可推出结果．‎ ‎【解答】解：四棱锥的三视图对应的直观图为：PA⊥底面ABCD，‎ AC=，CD=，‎ PC=3，PD=2，可得三角形PCD不是直角三角形．‎ 所以侧面中有3个直角三角形，分别为：△PAB，△PBC，‎ ‎△PAD．‎ 故选：C．‎ ‎【点评】本题考查简单几何体的三视图的应用，是基本知识的考查．‎ ‎　‎ ‎6．（5分）设，均为单位向量，则“|﹣3|=|3+|”是“⊥”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【分析】根据向量数量积的应用，结合充分条件和必要条件的对应进行判断即可．‎ ‎【解答】解：∵“|﹣3|=|3+|”‎ ‎∴平方得||2+9||2﹣6•=9||2+||2+6•，‎ 即1+9﹣6•=9+1+6•，‎ 即12•=0，‎ 则•=0，即⊥，‎ 则“|﹣3|=|3+|”是“⊥”的充要条件，‎ 故选：C．‎ ‎【点评】本题主要考查充分条件和必要条件的判断，结合向量数量积的公式进行转化是解决本题的关键．‎ ‎　‎ ‎7．（5分）在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线x﹣my﹣2=0的距离．当θ、m变化时，d的最大值为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【分析】由题意d==，当sin（θ+α）=﹣1时，dmax=1+≤3．由此能求出d的最大值．‎ ‎【解答】解：由题意d==，‎ tanα==，‎ ‎∴当sin（θ+α）=﹣1时，‎ dmax=1+≤3．‎ ‎∴d的最大值为3．‎ 故选：C．‎ ‎【点评】本题考查点到直线的距离的最大值的求法，考查点到直线的距离公式、三角函数性质等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．‎ ‎　‎ ‎8．（5分）设集合A={（x，y）|x﹣y≥1，ax+y＞4，x﹣ay≤2}，则（　　）‎ A．对任意实数a，（2，1）∈A B．对任意实数a，（2，1）∉A C．当且仅当a＜0时，（2，1）∈A D．当且仅当a≤时，（2，1）∉A ‎【分析】利用a的取值，反例判断（2，1）∈A是否成立即可．‎ ‎【解答】解：当a=﹣1时，集合A={（x，y）|x﹣y≥1，ax+y＞4，x﹣ay≤2}={（x，y）|x﹣y≥1，﹣x+y＞4，x+y≤2}，显然（2，1）不满足，﹣x+y＞4，x+y≤2，所以A，C不正确；‎ 当a=4，集合A={（x，y）|x﹣y≥1，ax+y＞4，x﹣ay≤2}={（x，y）|x﹣y≥1，4x+y＞4，x﹣4y≤2}，显然（2，1）在可行域内，满足不等式，所以B不正确；‎ 故选：D．‎ ‎【点评】‎ 本题考查线性规划的解答应用，利用特殊点以及特殊值转化求解，避免可行域的画法，简洁明了．‎ ‎　‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎9．（5分）设{an}是等差数列，且a1=3，a2+a5=36，则{an}的通项公式为　an=6n﹣3　．‎ ‎【分析】利用等差数列通项公式列出方程组，求出a1=3，d=6，由此能求出{an}的通项公式．‎ ‎【解答】解：∵{an}是等差数列，且a1=3，a2+a5=36，‎ ‎∴，‎ 解得a1=3，d=6，‎ ‎∴an=a1+（n﹣1）d=3+（n﹣1）×6=6n﹣3．‎ ‎∴{an}的通项公式为an=6n﹣3．‎ 故答案为：an=6n﹣3．‎ ‎【点评】本题考查等差数列的通项公式的求法，考查等差数列的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．‎ ‎　‎ ‎10．（5分）在极坐标系中，直线ρcosθ+ρsinθ=a（a＞0）与圆ρ=2cosθ相切，则a=　1+　．‎ ‎【分析】首先把曲线和直线的极坐标方程转化成直角坐标方程，进一步利用圆心到直线的距离等于半径求出结果．‎ ‎【解答】解：圆ρ=2cosθ，‎ 转化成：ρ2=2ρcosθ，‎ 进一步转化成直角坐标方程为：（x﹣1）2+y2=1，‎ 把直线ρ（cosθ+sinθ）=a的方程转化成直角坐标方程为：x+y﹣a=0．‎ 由于直线和圆相切，‎ 所以：利用圆心到直线的距离等于半径．‎ 则：=1，‎ 解得：a=1±．a＞0‎ 则负值舍去．‎ 故：a=1+．‎ 故答案为：1+．‎ ‎【点评】本题考查的知识要点：极坐标方程与直角坐标方程的互化，直线与圆相切的充要条件的应用．‎ ‎　‎ ‎11．（5分）设函数f（x）=cos（ωx﹣）（ω＞0），若f（x）≤f（）对任意的实数x都成立，则ω的最小值为　　．‎ ‎【分析】利用已知条件推出函数的最大值，然后列出关系式求解即可．‎ ‎【解答】解：函数f（x）=cos（ωx﹣）（ω＞0），若f（x）≤f（）对任意的实数x都成立，‎ 可得：，k∈Z，解得ω=，k∈Z，ω＞0‎ 则ω的最小值为：．‎ 故答案为：．‎ ‎【点评】本题考查三角函数的最值的求法与应用，考查转化思想以及计算能力．‎ ‎　‎ ‎12．（5分）若x，y满足x+1≤y≤2x，则2y﹣x的最小值是　3　．‎ ‎【分析】作出不等式组对应的平面区域，利用目标函数的几何意义进行求解即可．‎ ‎【解答】解：作出不等式组对应的平面区域如图：‎ 设z=2y﹣x，则y=x+z，‎ 平移y=x+z，‎ 由图象知当直线y=x+z经过点A时，‎ 直线的截距最小，此时z最小，‎ 由得，即A（1，2），‎ 此时z=2×2﹣1=3，‎ 故答案为：3‎ ‎【点评】本题主要考查线性规划的应用，利用目标函数的几何意义以及数形结合是解决本题的关键．‎ ‎　‎ ‎13．（5分）能说明“若f（x）＞f（0）对任意的x∈（0，2]都成立，则f（x）在[0，2]上是增函数”为假命题的一个函数是　f（x）=sinx　．‎ ‎【分析】本题答案不唯一，符合要求即可．‎ ‎【解答】解：例如f（x）=sinx，‎ 尽管f（x）＞f（0）对任意的x∈（0，2]都成立，‎ 当x∈[0，）上为增函数，在（，2]为减函数，‎ 故答案为：f（x）=sinx．‎ ‎【点评】本题考查了函数的单调性，属于基础题．‎ ‎　‎ ‎14．（5分）已知椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为　　；双曲线N的离心率为　2　．‎ ‎【分析】‎ 利用已知条件求出正六边形的顶点坐标，代入椭圆方程，求出椭圆的离心率；利用渐近线的夹角求解双曲线的离心率即可．‎ ‎【解答】解：椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，‎ 可得椭圆的焦点坐标（c，0），正六边形的一个顶点（，），可得：，可得，可得e4﹣8e2+4=0，e∈（0，1），‎ 解得e=．‎ 同时，双曲线的渐近线的斜率为，即，‎ 可得：，即，‎ 可得双曲线的离心率为e==2．‎ 故答案为：；2．‎ ‎【点评】本题考查椭圆以及双曲线的简单性质的应用，考查计算能力．‎ ‎　‎ 三、解答题共6小题，共80分。解答应写出文字说明，演算步骤或证明过程。‎ ‎15．（13分）在△ABC中，a=7，b=8，cosB=﹣．‎ ‎（Ⅰ）求∠A；‎ ‎（Ⅱ）求AC边上的高．‎ ‎【分析】（Ⅰ）由正弦定理结合大边对大角进行求解即可．‎ ‎（Ⅱ）利用余弦定理求出c的值，结合三角函数的高与斜边的关系进行求解即可．‎ ‎【解答】解：（Ⅰ）∵a＜b，∴A＜B，即A是锐角，‎ ‎∵cosB=﹣，∴sinB===，‎ 由正弦定理得=得sinA===，‎ 则A=．‎ ‎（Ⅱ）由余弦定理得b2=a2+c2﹣2accosB，‎ 即64=49+c2+2×7×c×，‎ 即c2+2c﹣15=0，‎ 得（c﹣3）（c+5）=0，‎ 得c=3或c=﹣5（舍），‎ 则AC边上的高h=csinA=3×=．‎ ‎【点评】本题主要考查解三角形的应用，利用正弦定理以及余弦定理建立方程关系是解决本题的关键．‎ ‎　‎ ‎16．（14分）如图，在三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB=BC=，AC=AA1=2．‎ ‎（Ⅰ）求证：AC⊥平面BEF；‎ ‎（Ⅱ）求二面角B﹣CD﹣C1的余弦值；‎ ‎（Ⅲ）证明：直线FG与平面BCD相交．‎ ‎【分析】（I）证明AC⊥BE，AC⊥EF即可得出AC⊥平面BEF；‎ ‎（II）建立坐标系，求出平面BCD的法向量，通过计算与的夹角得出二面角的大小；‎ ‎（III）计算与的数量积即可得出结论．‎ ‎【解答】（I）证明：∵E，F分别是AC，A1C1的中点，∴EF∥CC1，‎ ‎∵CC1⊥平面ABC，∴EF⊥平面ABC，‎ 又AC⊂平面ABC，∴EF⊥AC，‎ ‎∵AB=BC，E是AC的中点，‎ ‎∴BE⊥AC，‎ 又BE∩EF=E，BE⊂平面BEF，EF⊂平面BEF，‎ ‎∴AC⊥平面BEF．‎ ‎（II）解：以E为原点，以EB，EC，EF为坐标轴建立空间直角坐标系如图所示：‎ 则B（2，0，0），C（0，1，0），D（0，﹣1，1），‎ ‎∴=（﹣2，1，0），=（0，﹣2，1），‎ 设平面BCD的法向量为=（x，y，z），则，即，‎ 令y=2可得=（1，2，4），又EB⊥平面ACC1A1，‎ ‎∴=（2，0，0）为平面CD﹣C1的一个法向量，‎ ‎∴cos＜，＞===．‎ 由图形可知二面角B﹣CD﹣C1为钝二面角，‎ ‎∴二面角B﹣CD﹣C1的余弦值为﹣．‎ ‎（III）证明：F（0，0，2），（2，0，1），∴=（2，0，﹣1），‎ ‎∴•=2+0﹣4=﹣2≠0，‎ ‎∴与不垂直，‎ ‎∴FG与平面BCD不平行，又FG⊄平面BCD，‎ ‎∴FG与平面BCD相交．‎ ‎【点评】本题考查了线面垂直的判定，二面角的计算与空间向量的应用，属于中档题．‎ ‎　‎ ‎17．（12分）电影公司随机收集了电影的有关数据，经分类整理得到下表：‎ 电影类型 第一类 第二类 第三类 第四类 第五类 第六类 电影部数 ‎140‎ ‎50‎ ‎300‎ ‎200‎ ‎800‎ ‎510‎ 好评率 ‎0.4‎ ‎0.2‎ ‎0.15‎ ‎0.25‎ ‎0.2‎ ‎0.1‎ 好评率是指：一类电影中获得好评的部数与该类电影的部数的比值．‎ 假设所有电影是否获得好评相互独立．‎ ‎（Ⅰ）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；‎ ‎（Ⅱ）从第四类电影和第五类电影中各随机选取1部，估计恰有1部获得好评的概率；‎ ‎（Ⅲ）假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等．用“ξk=1”表示第k类电影得到人们喜欢．“ξk=0”表示第k类电影没有得到人们喜欢（k=1，2，3，4，5，6）．写出方差Dξ1，Dξ2，Dξ3，Dξ4，Dξ5，Dξ6的大小关系．‎ ‎【分析】（Ⅰ）先求出总数，再求出第四类电影中获得好评的电影的部数，利用古典概型概率计算公式直接求解．‎ ‎（Ⅱ）设事件B表示“从第四类电影和第五类电影中各随机选取1部，恰有1部获得好评”，第四类获得好评的有50部，第五类获得好评的有160部，由此能求出从第四类电影和第五类电影中各随机选取1部，估计恰有1部获得好评的概率．‎ ‎（Ⅲ）由题意知，定义随机变量如下：ξk=，则ξk服从两点分布，分别求出六类电影的分布列及方差由此能写出方差Dξ1，Dξ2，Dξ3，Dξ4，Dξ5，Dξ6的大小关系．‎ ‎【解答】解：（Ⅰ）设事件A表示“从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影”，‎ 总的电影部数为140+50+300+200+800+510=2000部，‎ 第四类电影中获得好评的电影有：200×0.25=50部，‎ ‎∴从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的频率为：‎ P（A）==0.025．‎ ‎（Ⅱ）设事件B表示“从第四类电影和第五类电影中各随机选取1部，恰有1部获得好评”，‎ 第四类获得好评的有：200×0.25=50部，‎ 第五类获得好评的有：800×0.2=160部，‎ 则从第四类电影和第五类电影中各随机选取1部，估计恰有1部获得好评的概率：‎ P（B）==0.35．‎ ‎（Ⅲ）由题意知，定义随机变量如下：‎ ξk=，‎ 则ξk服从两点分布，则六类电影的分布列及方差计算如下：‎ 第一类电影：‎ ‎ ξ1‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.4‎ ‎ 0.6‎ E（ξ1）=1×0.4+0×0.6=0.4，‎ D（ξ1）=（1﹣0.4）2×0.4+（0﹣0.4）2×0.6=0.24．‎ 第二类电影：‎ ‎ ξ2‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.2‎ ‎ 0.8‎ E（ξ2）=1×0.2+0×0.8=0.2，‎ D（ξ2）=（1﹣0.2）2×0.2+（0﹣0.2）2×0.8=0.16．‎ 第三类电影：‎ ‎ ξ3‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.15‎ ‎ 0.85‎ E（ξ3）=1×0.15+0×0.85=0.15，‎ D（ξ3）=（1﹣0.15）2×0.15+（0﹣0.85）2×0.85=0.1275．‎ 第四类电影：‎ ‎ ξ4‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.25‎ ‎ 0.75‎ E（ξ4）=1×0.25+0×0.75=0.15，‎ D（ξ4）=（1﹣0.25）2×0.25+（0﹣0.75）2×0.75=0.1875．‎ 第五类电影：‎ ‎ ξ5‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.2‎ ‎ 0.8‎ E（ξ5）=1×0.2+0×0.8=0.2，‎ D（ξ5）=（1﹣0.2）2×0.2+（0﹣0.2）2×0.8=0.16．‎ 第六类电影：‎ ‎ ξ6‎ ‎ 1‎ ‎ 0‎ ‎ P ‎ 0.1‎ ‎ 0.9‎ E（ξ6）=1×0.1+0×0.9=0.1，‎ D（ξ5）=（1﹣0.1）2×0.1+（0﹣0.1）2×0.9=0.09．‎ ‎∴方差Dξ1，Dξ2，Dξ3，Dξ4，Dξ5，Dξ6的大小关系为：‎ Dξ6＜Dξ3＜Dξ2=Dξ5＜Dξ4＜Dξ1．‎ ‎【点评】‎ 本题考查概率的求法，考查离散型随机变量的方差的求法，考查古典概型、两点分布等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．‎ ‎　‎ ‎18．（13分）设函数f（x）=[ax2﹣（4a+1）x+4a+3]ex．‎ ‎（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与x轴平行，求a；‎ ‎（Ⅱ）若f（x）在x=2处取得极小值，求a的取值范围．‎ ‎【分析】（Ⅰ）求得f（x）的导数，由导数的几何意义可得f′（1）=0，解方程可得a的值；‎ ‎（Ⅱ）求得f（x）的导数，注意分解因式，讨论a=0，a=，a＞，0＜a＜，a＜0，由极小值的定义，即可得到所求a的范围．‎ ‎【解答】解：（Ⅰ）函数f（x）=[ax2﹣（4a+1）x+4a+3]ex的导数为 f′（x）=[ax2﹣（2a+1）x+2]ex．‎ 由题意可得曲线y=f（x）在点（1，f（1））处的切线斜率为0，‎ 可得（a﹣2a﹣1+2）e=0，‎ 解得a=1；‎ ‎（Ⅱ）f（x）的导数为f′（x）=[ax2﹣（2a+1）x+2]ex=（x﹣2）（ax﹣1）ex，‎ 若a=0则x＜2时，f′（x）＞0，f（x）递增；x＞2，f′（x）＜0，f（x）递减．‎ x=2处f（x）取得极大值，不符题意；‎ 若a＞0，且a=，则f′（x）=（x﹣2）2ex≥0，f（x）递增，无极值；‎ 若a＞，则＜2，f（x）在（，2）递减；在（2，+∞），（﹣∞，）递增，‎ 可得f（x）在x=2处取得极小值；‎ 若0＜a＜，则＞2，f（x）在（2，）递减；在（，+∞），（﹣∞，2）递增，‎ 可得f（x）在x=2处取得极大值，不符题意；‎ 若a＜0，则＜2，f（x）在（，2）递增；在（2，+∞），（﹣∞，）递减，‎ 可得f（x）在x=2处取得极大值，不符题意．‎ 综上可得，a的范围是（，+∞）．‎ ‎【点评】本题考查导数的运用：求切线的斜率和极值，考查分类讨论思想方法，以及运算能力，属于中档题．‎ ‎　‎ ‎19．（14分）已知抛物线C：y2=2px经过点P（1，2），过点Q（0，1）的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N．‎ ‎（Ⅰ）求直线l的斜率的取值范围；‎ ‎（Ⅱ）设O为原点，=λ，=μ，求证：+为定值．‎ ‎【分析】（Ⅰ）将P代入抛物线方程，即可求得p的值，设直线AB的方程，代入椭圆方程，由△＞0，即可求得k的取值范围；‎ ‎（Ⅱ）根据向量的共线定理即可求得λ=1﹣yM，μ=1﹣yN，求得直线PA的方程，令x=0，求得M点坐标，同理求得N点坐标，根据韦达定理即可求得+为定值．‎ ‎【解答】解：（Ⅰ）∵抛物线C：y2=2px经过点 P（1，2），∴4=2p，解得p=2，‎ 设过点（0，1）的直线方程为y=kx+1，‎ 设A（x1，y1），B（x2，y2）‎ 联立方程组可得，‎ 消y可得k2x2+（2k﹣4）x+1=0，‎ ‎∴△=（2k﹣4）2﹣4k2＞0，且k≠0解得k＜1，‎ 且k≠0，x1+x2=﹣，x1x2=，‎ 故直线l的斜率的取值范围（﹣∞，0）∪（0，1）；‎ ‎（Ⅱ）证明：设点M（0，yM），N（0，yN），‎ 则=（0，yM﹣1），=（0，﹣1）‎ 因为=λ，所以yM﹣1=﹣yM﹣1，故λ=1﹣yM，同理μ=1﹣yN，‎ 直线PA的方程为y﹣2=（x﹣1）=（x﹣1）=（x﹣1），‎ 令x=0，得yM=，同理可得yN=，‎ 因为+=+=+======2，‎ ‎∴+=2，∴+为定值．‎ ‎【点评】本题考查抛物线的方程，直线与抛物线的位置关系，考查韦达定理的应用，考查转化思想，计算能力，属于中档题．‎ ‎　‎ ‎20．（14分）设n为正整数，集合A={α|α=（t1，t2，…tn），tk∈{0，1}，k=1，2，…，n}，对于集合A中的任意元素α=（x1，x2，…，xn）和β=（y1，y2，…yn ‎），记 M（α，β）=[（x1+y1﹣|x1﹣y1|）+（x2+y2﹣|x2﹣y2|）+…（xn+yn﹣|xn﹣yn|）]‎ ‎（Ⅰ）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（α，β）的值；‎ ‎（Ⅱ）当n=4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数．求集合B中元素个数的最大值；‎ ‎（Ⅲ）给定不小于2的n，设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）=0，写出一个集合B，使其元素个数最多，并说明理由．‎ ‎【分析】（Ⅰ）直接根据定义计算．‎ ‎（Ⅱ）注意到1的个数的奇偶性，根据定义反证证明．‎ ‎（Ⅲ）根据抽屉原理即可得证．‎ ‎【解答】解：（I ） M（α，α）=1+1+0=2，M（α，β）=0+1+0=1．‎ ‎（II）考虑数对（xk，yk）只有四种情况：（0，0）、（0，1）、（1，0）、（1，1），相应的分别为0、0、0、1，‎ 所以B中的每个元素应有奇数个1，‎ 所以B中的元素只可能为（上下对应的两个元素称之为互补元素）：‎ ‎（1，0，0，0 ）、（0，1，0，0）、（0，0，1，0）、（0，0，0，1），‎ ‎（0，1，1，1）、（1，0，1，1）、（1，1，0，1）、（1，1，1，0），‎ 对于任意两个只有1个1的元素α，β都满足M（α，β）是偶数，‎ 所以四元集合B={（1，0，0，0）、（0，1，0，0）、（0，0，1，0）、（0，0，0，1）}满足 题意，‎ 假设B中元素个数大于等于4，就至少有一对互补元素，‎ 除了这对互补元素之外还有至少1个含有3个1的元素α，‎ 则互补元素中含有1个1的元素β与之满足M（α，β）=1不合题意，‎ 故B中元素个数的最大值为4．‎ ‎（Ⅲ） B={‎ ‎（0，0，0，…0），（1，0，0…，0），（0，1，0，…0），（0，0，1…0）…，‎ ‎（0，0，0，…，1）}，‎ 此时B中有n+1个元素，下证其为最大．‎ 对于任意两个不同的元素α，β，满足M（α，β）=0，则α，β中相同位置上的数字不能同时为1，‎ 假设存在B有多于n+1个元素，由于α=（0，0，0，…，0）与任意元素β都有M（α，β）=0，‎ 所以除（0，0，0，…，0）外至少有n+1个元素含有1，‎ 根据元素的互异性，至少存在一对α，β满足xi=yi=l，此时M（α，β）≥1不满足题意，‎ 故B中最多有n+1个元素．‎ ‎【点评】本题主要考查集合的含义与表示、集合的运算以及集合之间的关系．综合性较强，难度较大．‎ ‎　‎