备战2020年高考数学大一轮复习 热点聚焦与扩展 专题26 应用AD=xAB+yAC解题探秘

备战2020年高考数学大一轮复习 热点聚焦与扩展 专题26 应用AD=xAB+yAC解题探秘

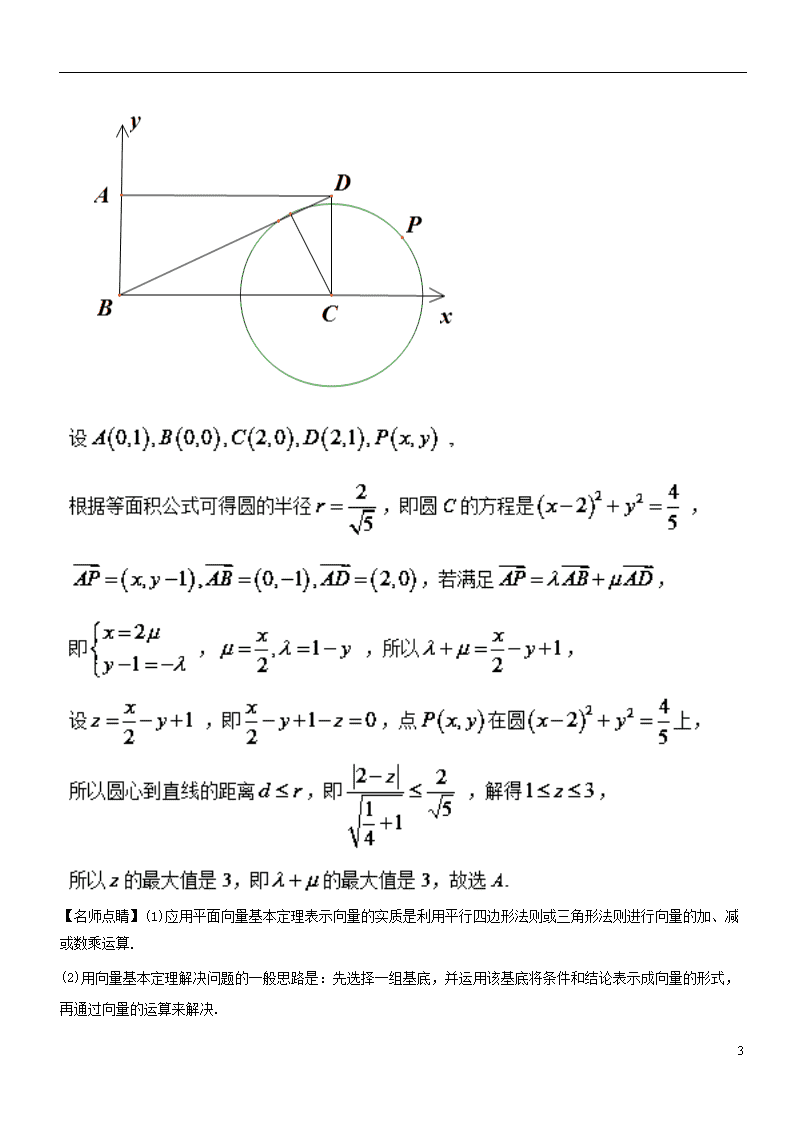
专题26 应用 解题探秘 ‎【热点聚焦与扩展】‎ 高考对平面向量基本定理的考查，往往以选择题或填空题的形式出现.常以平面图形为载体，借助于向量的坐标形式等考查共线、垂直等问题；也易同三角函数、解析几何等知识相结合，以工具的形式出现．用平面向量基本定理解决问题的一般思路是：先选择一组基底，再用该基底表示向量，其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算．要特别注意基底的不唯一性-----只要两个向量不共线，就可以作为平面的一组基底，对基底的选取不唯一，平面内任意向量都可被这个平面的一组基底线性表示，且在基底确定后，这样的表示是唯一的．‎ ‎1、平面向量基本定理：若平面上两个向量不共线，则对平面上的任一向量，均存在唯一确定的，（其中），使得.其中称为平面向量的一组基底.‎ ‎（1）不共线的向量即可作为一组基底表示所有的向量 ‎（2）唯一性：若且，则 ‎2、“爪”字型图及性质：‎ ‎（1）已知为不共线的两个向量，则对于向量，必存在，使得.则三点共线 当，则与位于同侧，且位于与之间 当，则与位于两侧 ‎ 时，当，则在线段上；当，则在线段延长线上 ‎（2）已知在线段上，且，则 ‎3、中确定方法 ‎（1）在几何图形中通过三点共线即可考虑使用“爪”字型图完成向量的表示，进而确定 18‎ ‎（2）若题目中某些向量的数量积已知，则对于向量方程，可考虑两边对同一向量作数量积运算，从而得到关于的方程，再进行求解 ‎（3）若所给图形比较特殊（矩形，特殊梯形等），则可通过建系将向量坐标化，从而得到关于的方程，再进行求解 ‎【经典例题】‎ 例1.在梯形ABCD中，AD∥BC，已知AD＝4，BC＝6，若 (m，n∈R)，则＝(　　)‎ A. －3 B. － C. D. 3‎ ‎【答案】A ‎【点睛】当向量等式中的向量系数含参时，可通过对两边作同一向量的数量积运算便可得到关于系数的方程.若要解出系数，则可根据字母的个数确定构造方程的数量 例2.【2017课标3，理12】在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上.若= +，则+的最大值为（ ）‎ A．3 B．2 C． D．2‎ ‎【答案】A ‎【解析】如图所示，建立平面直角坐标系 18‎ ‎【名师点睛】(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.‎ ‎(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决.‎ 18‎ 例3.【2019届安徽省淮南市高三第一次（2月）模拟】已知是的重心，过点作直线与，交于点，且，，，则的最小值是( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 如图 三点共线， ‎ ‎ ∵是的重心，‎ 故 ‎ 当且仅当等号成立 故选D 例4.【2019届北京市朝阳区一模】在平面直角坐标系中,已知点, ,动点满足 ,其中,则所有点构成的图形面积为( )‎ A. B. C. D. ‎ 18‎ ‎【答案】C ‎【解析】设,则,‎ ‎ , ,所有点构成图形如图所示（阴影部分）,‎ ‎,故选.‎ ‎【方法点睛】本题主要考查平面向量基本定理以及线性规划的应用及数学的转化与划归思想.属于难题.转化与划归思想解决高中数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透，这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域，进而顺利解答，希望同学们能够熟练掌握并应用于解题当中.本题中，把向量问题转化为线性规划问题解答是解题的关键.‎ 例5.【2019年4月湖南G10教育联盟高三联考】平行四边形中， ， ， ， 是平行四边形内一点，且，如，则的最大值为（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】B ‎【解析】∵，‎ 18‎ ‎∴=‎ ‎=‎ 故选：B．‎ 例6.【2019届四川省雅安市三诊】在直角梯形，，，，，，分别为，的中点，点在以为圆心，为半径的圆弧上变动（如图所示）.若，其中，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】建立如图所示的坐标系：‎ 18‎ 则，，，，，即，，.‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ 故选A.‎ 例7.在中，为边的中点，为的中点，过点作一直线分别交于点，若，则的最小值是（ ）‎ A. B. C. D. ‎ ‎【答案】‎ 18‎ ‎【解析】若要求出的最值，则需从条件中得到的关系。由共线可想到“爪”字型图，所以，其中，下面考虑将的关系转为的关系。利用条件中的向量关系：且，所以，因为，所以，由平面向量基本定理可得：，所以，所以，而，所以 答案：A 例8.【2017天津，文理】在中，，，.若，，且，则的值为___________.‎ ‎【答案】 ‎ ‎【名师点睛】根据平面向量的基本定理，利用表示平面向量的一组基地可以表示平面内的任一向量，利用向量的定比分点公式表示向量，计算数量积，选取基底很重要，本题的已知模和夹角，选作基底易于计算数量积.‎ 例9.【2019年衡水金卷调研卷三】如图所示，已知在中， ， ， 交于点， ，则__________．‎ 18‎ ‎【答案】‎ ‎【解析】设,,‎ 即，∴，由三点共线，得，‎ 解得.又 ‎∴‎ ‎∴‎ 例10.【2019届江西省吉安一中、九江一中等八所重点中学高三4月联考】点为所在平面内一动点，且满足： ， ， 若点的轨迹与直线围成封闭区域的面积为，则__________．‎ ‎【答案】‎ ‎【解析】设， ，则.‎ ‎∵满足： ‎ 18‎ ‎∴，即.‎ ‎∴‎ ‎∴为等边三角形 ‎∴‎ 故答案为.‎ 点睛：本题考查学生的是三角形面积公式与向量的交汇处，属于中档题目.由为突破点，构造出是解题的关键，由系数和为得出三点共线，可得的轨迹为直线，结合三角形面积公式即可.‎ ‎【精选精练】‎ ‎1．【2019届辽宁省朝阳市普通高中一模】在中，为的重心，过点的直线分别交，于，两点，且，，则（ ）‎ A. B. C. D. ‎ ‎【答案】A 18‎ ‎2．【2019届河北省武邑中学高三下期中】已知在中，两直角边， ， 是内一点，且，设，则（ ）‎ A. B. C. 3 D. ‎ ‎【答案】A ‎【解析】分析：建立平面直角坐标系，分别写出B、C点坐标，由于∠DAB=60°，设D点坐标为（m， ），由平面向量坐标表示，可求出λ和μ．‎ 详解：如图以A为原点，以AB所在的直线为x轴，以AC所在的直线为y轴建立平面直角坐标系，则B点坐标为（1，0），C点坐标为（0，2），‎ 因为∠DAB=60°，设D点坐标为（m， ），‎ ‎=λ（1，0）+μ（0，2）=（λ，2μ）⇒λ=m，μ= ，‎ 则．‎ 故选A．‎ ‎3．【2019届衡水金卷】在平面直角坐标系中，为坐标原点，，，，‎ 18‎ ‎，设，，若，，且，则的最大值为（ ）‎ A. 7 B. 10 C. 8 D. 12‎ ‎【答案】B 点睛：利用线性规划求最值的步骤：(1)在平面直角坐标系内作出可行域;(2)考虑目标函数的几何意义，将目标函数进行变形．常见的类型有截距型（型）、斜率型（型）和距离型（型）;(3)确定最优解：根据目标函数的类型，并结合可行域确定最优解;(4)求最值：将最优解代入目标函数即可求出最大值或最小值;注意解答本题时不要忽视斜率不存在的情形.‎ ‎4．【2019届安徽省安庆市二模】在中，点是边上任意一点， 是线段的中点，若存在实数和，使得，则（ ）‎ A. B. 2 C. 2 D. ‎ ‎【答案】B 18‎ 又，所以， ，‎ 所以. 故选B.‎ ‎5．【2019届北京市九中十月月考】如图,半径为的扇形的圆心角为,点在上,且,若,则 ( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎， ，故选A.‎ ‎【 ‎ 18‎ 方法点睛】本题主要考查向量的坐标运算、相等向量以及平面向量基本定理，属于难题．向量的运算有两种方法，一是几何运算往往结合平面几何知识和三角函数知识解答，运算法则是：（１）平行四边形法则（平行四边形的对角线分别是两向量的和与差）；（２）三角形法则（两箭头间向量是差，箭头与箭尾间向量是和）；二是坐标运算：建立坐标系转化为解析几何或者三角函数问题解答 ‎6.【2019年辽宁省部分重点中学协作体高三模拟】已知是边长为1的正三角形，若点满足，则的最小值为（ ）‎ A. B. 1 C. D. ‎ ‎【答案】C ‎【解析】分析：以为原点，以为轴，建立坐标系，可得， ，利用配方法可得的最小值.‎ 详解：以为原点，以为轴，建立坐标系，‎ 为边长为的正三角形，，‎ 点睛：本题主要考查向量的模与平面向量的坐标运算，属于难题．向量的运算有两种方法，一是几何运算，往往结合平面几何知识和三角函数知识解答，运算法则是：（１）平行四边形法则；（２）三角形法则；二是坐标运算：建立坐标系转化为解析几何问题解答（求最值与求范围问题往往运用坐标运算来解答）.‎ ‎7．【2019届衡水金卷二】已知在中，为边上的点，，若，则__________．‎ 18‎ ‎【答案】‎ ‎【解析】因为，所以，所以，所以，所以，故答案为.‎ ‎8．【2019届四川省德阳市二诊】如图，在三角形中，、分别是边、的中点，点在直线上，且 ，则代数式的最小值为__________．‎ ‎【答案】‎ ‎【解析】因为点共线，所以由，有 又因为、分别是边、的中点， 所以 ‎ 18‎ ‎【点睛】本题主要考查了平面向量的应用，解题的关键是向量共线定理的应用及结论“点共线，由，有”的应用 ‎9．【2019届四川省高三“联测促改”活动】在平面向量中有如下定理：设点、、、为同一平面内的点，则、、三点共线的充要条件是：存在实数，使.试利用该定理解答下列问题：如图，在中，点为边的中点，点在边上，且， 交于点，设，则__________．‎ ‎【答案】‎ ‎【解析】∵三点共线，‎ ‎∴， ．‎ 答案： ‎ ‎10．【2019届北京市北京166中高三10月考】如图,在矩形中,点、分别在线段、‎ 18‎ 上,且满足,若,则___________; ___________.‎ ‎【答案】 0 ‎ ‎【解析】.‎ ‎，‎ 又∴两式相加得 即 点睛：(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．‎ ‎(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．‎ ‎11．【2019年齐鲁名校教科研协作体 山东、湖北部分重点中学高考冲刺模拟】已知G为△ABC的重心，点M，N分别在边AB，AC上，满足其中则△ABC和△AMN的面积之比为_______.‎ ‎【答案】‎ 18‎ ‎【解析】连接并延长交于，此时为的中点，故 ‎，设 ， ， ，又，解得，‎ 则，故答案为.‎ ‎12．【2019届山东省菏泽市一模】已知在△ABC中，D为边BC上的点，且BD=3DC，点E为AD的中点，，则=_________.‎ ‎【答案】‎ ‎【解析】如图：‎ 18‎