全国高考理科数学历年试题分类汇编

全国高考理科数学历年试题分类汇编

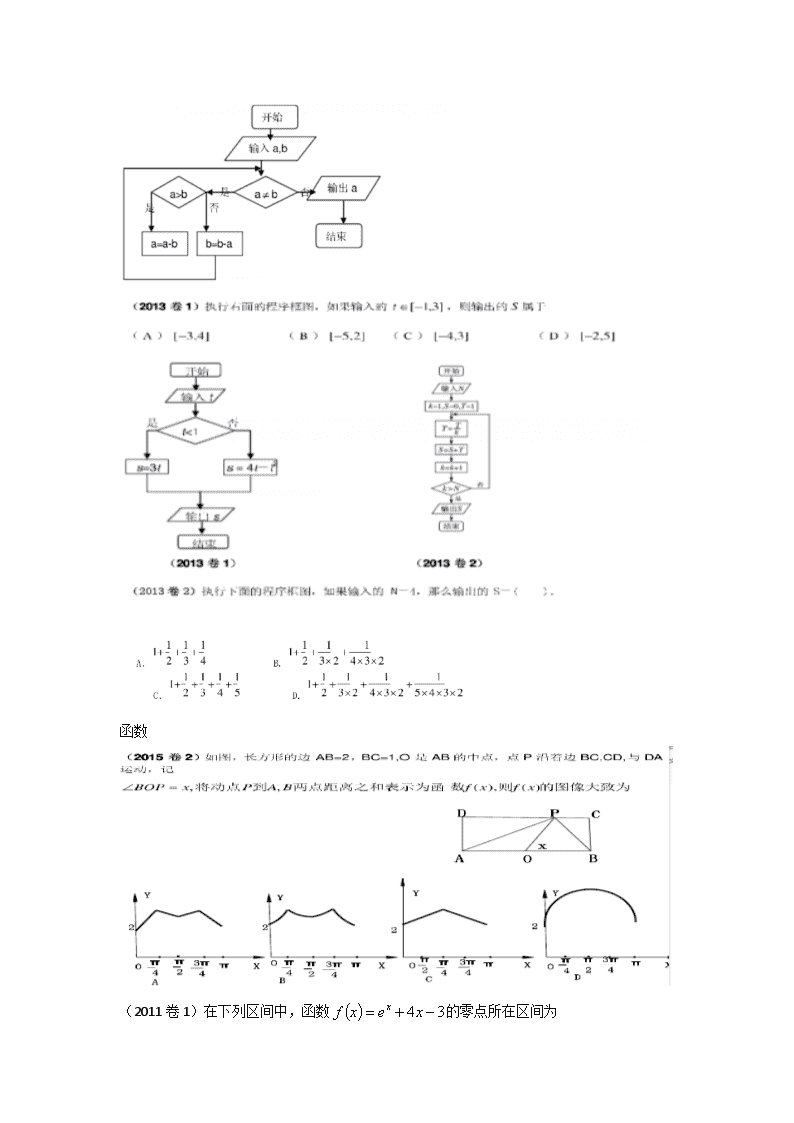
全国高考理科数学历年试题分类汇编 ‎ （一） 小题分类 ‎ 集合 （2015卷1）已知集合A={xx=3n+2,nN},B={6,8,10,12,14}，则集合AB中的元素个（    ）（A） 5   （B）4 （C）3  （D）2 ‎ 1. ‎（2013卷2）已知集合M＝{x|－3＜x＜1}，N＝{－3，－2，－1,0,1}，则M∩N＝(  )． A．{－2，－1,0,1}  B．{－3，－2，－1,0}  C．{－2，－1,0}     D．{－3，－2，－1} ‎ 2. ‎（2009卷1）已知集合A=1,3,5,7,9},B={0,3,6,9,12}，则AB= ‎ A．{3，5}    B．{3，6}    C．{3，7}    D．{3，9}  ‎ 3. ‎（2008卷1）已知集合M ={ x|(x + 2)(x－1) < 0 }，N ={ x| x + 1 < 0 }，则M∩N =（    ） {A. (－1，1)   B. (－2，1)   C. (－2，－1)  D. (1，2) ‎ 复数 1. ‎（2015卷1）已知复数z满足(z-1)i=1+i，则z=（  ）‎ ‎ （A） -2-i   （B）-2+i    （C）2-i     （D）2+i ‎ 2. ‎（2015卷2）若a实数，且 =3+i,则a=（   ）   A.-4    B. -3    C. 3     D.  4 ‎ 3. ‎（2010卷1）已知复数，其中（ ）‎ A= B= C=1 D=2‎ 向量 1. ‎（2015卷1）已知点A(0,1),B(3,2)，向量=(-4,-3)，则向量= ( ) ‎ （A） ‎(-7,-4) （B）(7,4) （C）(-1,4) （D）(1,4) ‎ 2. ‎（2015卷2）已知向量=(0,-1),=(-1,2),则=( )‎ A. ‎-1 B. 0 C. 1 D. 2‎ 3. ‎（2013卷3）已知两个单位向量，的夹角为60度，，那么t=‎ 程序框图 ‎（2015卷2）右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。执行该程序框图，若输入的a,b分别为14,18，则输出的a为 A . 0 B. 2 C. 4 D.14‎ 函数 ‎（2011卷1）在下列区间中，函数的零点所在区间为 A. ‎ B . C. D.‎ ‎（2010卷1）已知函数，若啊a,b,c,互不相等，且，则的取值范围是（ ）‎ A.（1,10） B.（5,6） C.（10,12） D.（20,24）‎ 导数 ‎（2015卷2）已知曲线y=x+lnx在点（1,1）处的切线与曲线相切，则 ‎（2014卷1）若函数在区间（1，）单调递增，则k的取值范围（ ）‎ A. ‎ B. C. D. ‎ ‎（2012卷1）设函数的最大值M，最小值N，则M+N=‎ 三角函数与解三角形 在锐角中，若，则的范围 （ ）‎ ‎（A） （B） （C） （D） ‎ ‎（2015卷1）函数的部分图像如图所示，则的递减区间为（ ）‎ 不等式 概率统计 ‎（2015卷1）如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1,2,3,4,5中任取3个不同的数，则这3个数构成一组勾股数的概率为（ ）‎ A. ‎ B. C. D.‎ ‎（2012卷2）6位选手依次演讲，其中选手甲不再第一个也不再最后一个演讲，则不同的演讲次序共有 （A）240种 （B）360种 （C）480种 （D）720种 ‎（2010卷1）设y＝f(x)为区间[0,1]上的连续函数，且恒有0≤f(x)≤1，可以用随机模拟方法近似计算积分.先产生两组(每组N个)区间[0,1]上的均匀随机数x1，x2，„‎ ‎，xN和y1，y2，„，yN，由此得到N个点(xi，yi)(i＝1,2，„，N)．再数出其中满足yi≤f(xi)(i＝1,2，„，N)的点数N1，那么由随机模拟方法可得积分的近似值为________．‎ 立体几何 ‎（2015卷2）已知A,B是球O的球面上两点，AOB=90°,C为该球面上动点，若三棱锥O-ABC 体积的最大值为36，则球O的表面积为 A. 36π B. 64π C. 144π D.256π ‎（2014卷2）正三棱柱-的底面边长为2，侧棱长为，则三棱锥A-的体积为 （A）3 （B） （C）1 （D）‎ 平面几何与圆锥曲线 数列 大题分类 三角函数 ‎1、9、如图，，是半个单位圆上的动点，是等边三角形，求当等于多少时，四边形的面积最大，并求四边形面积的最大值．‎ ‎2、（2017卷三）△ABC的内角A，B，C的对边分别为a，b，c，已知sinA+ cosA=0，a=2,b=2.‎ ‎（1）求c；‎ ‎（2）设D为BC边上一点，且AD AC,求△ABD的面积.‎ ‎3、在平面直角坐标系中，设锐角的始边与轴的非负半轴重合，终边与单位圆交于点，将射线绕坐标原点按逆时针方向旋转后与单位圆交于点. 记.‎ ‎（1）求函数的值域；‎ ‎（2）设的角所对的边分别为，若，且，，求.‎ 1. ‎4、在锐角△ABC中，分别为∠A、∠B、∠C所对的边，且 ‎（1）确定∠C的大小；‎ ‎（2）若c＝，求△ABC周长的取值范围．‎ 空间几何体 ‎1、如图，在四棱锥P-ABCD中，AB//CD，且 ‎(1)证明：平面PAB⊥平面PAD；‎ ‎(2)若PA=PD=AB=DC,,求二面角A-PB-C的余弦值.‎ ‎2、如图，四棱锥P-ABCD中，侧面PAD为等比三角形且垂直于底面三角形BCD， E是PD的中点 ‎（1）证明：学|科网直线 平面PAB ‎（2）点M在棱PC 上，且直线BM与底面ABCD所成锐角为 ，求二面角M-AB-D的余弦值 ‎3、如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．‎ ‎（1）证明：平面ACD⊥平面ABD；‎ ‎（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C 数列、2017年没有考大题 ‎1、设数列{an}（n=1，2，3，…）的前n项和Sn满足Sn=2an﹣a1，且a1，a2+1，a3成等差数列．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）记数列{}的前n项和为Tn，求使得|Tn﹣1|成立的n的最小值．‎ 1. ‎2、已知数列{an}和{bn}满足a1=2，b1=1，an+1=2an（n∈N*），b1+b2+b3+…+bn=bn+1﹣1（n∈‎ N*）‎ ‎（Ⅰ）求an与bn；‎ ‎（Ⅱ）记数列{anbn}的前n项和为Tn，求Tn．‎ 概率分布 ‎1、淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取100 个网箱，测量各箱水产品的产量（单位：kg）某频率直方图如下：‎ （1） 设两种养殖方法的箱产量相互独立，记A表示事件：旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A的概率；‎ （2） 填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：‎ （3） 根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）‎ ‎2、为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2)．‎ ‎（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数，求P(X≥1)及X的数学期望；学科&网（2）一天内抽检零件中，如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性；‎ ‎（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：‎ ‎9.95‎ ‎10.12‎ ‎9.96‎ ‎9.96‎ ‎10.01‎ ‎9.92‎ ‎9.98‎ ‎10.04‎ ‎10.26‎ ‎9.91‎ ‎10.13‎ ‎10.02‎ ‎9.22‎ ‎10.04‎ ‎10.05‎ ‎9.95‎ 经计算得，，其中xi为抽取的第i个零件的尺寸，i=1,2,…,16．‎ 用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对当天的生产过程进行检查？剔除之外的数据，用剩下的数据估计μ和σ（精确到0.01）．‎ 附：若随机变量Z服从正态分布N(μ,σ2)，则P(μ–3σb>0），四点P1（1,1），P2（0,1），P3（–1， ），P4（1，）中恰有三点在椭圆C上.‎ ‎（1）求C的方程；（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.‎ 1. 如图，已知直线L：的右焦点F，且交椭圆C于A、B两点，点A、B在直线上的射影依次为点D、E。‎ ‎（1）若抛物线的焦点为椭圆C的上顶点，求椭圆C的方程；‎ ‎（2）（理）连接AE、BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由。‎ ‎（文）若为x轴上一点,求证:‎ 导函数 ‎1、已知函数 x﹣1﹣alnx.‎ （1） 若 ，求a的值；‎ （2） 设m为整数，且对于任意正整数n， ﹤m，求m最小值.‎ ‎2、已知函数且.‎ ‎（1）求a；‎ ‎（2）证明：存在唯一的极大值点，且.‎ ‎3、已知函数=ae2x+（a﹣2）ex﹣x.‎ （1） 讨论的单调性；‎ （2） 若有两个零点，求a的取值范围.‎