高考理科数学真题演练分类解析平面向量的数量积及平面向量的应用21106

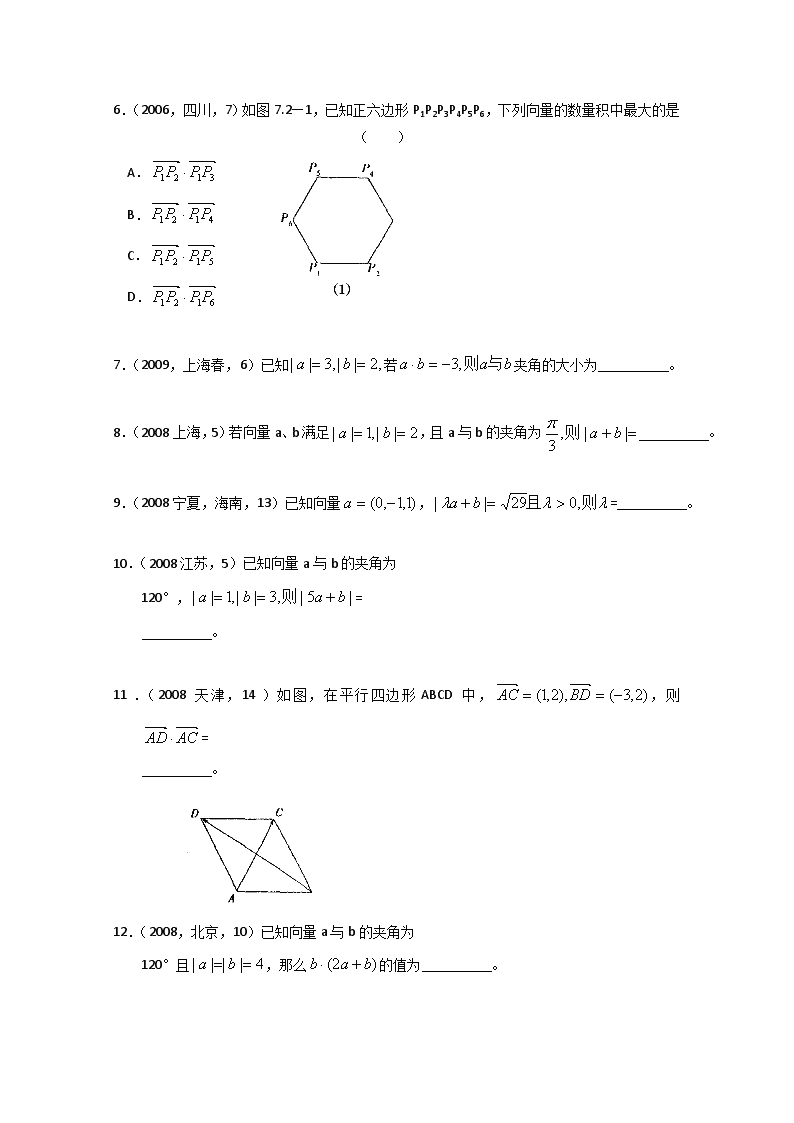
高考理科数学真题演练分类解析平面向量的数量积及平面向量的应用21106

‎【考点17】 平面向量的数量积及平面向量的应用 ‎1． （2009·江苏卷·2）已知向量a和向量b的夹角为30°，｜a｜=2，｜b｜=，则向量a和向量b的数量积a·b= ．‎ ‎2． （2009·海南宁夏卷·理·9）已知O，N，P在所在平面内，且，且，则点O，N，P依次是的（ ）‎ A．重心 外心 垂心 ‎ B．重心 外心 内心 ‎ C．外心 重心 垂心 ‎ D．外心 重心 内心 ‎（注：三角形的三条高线交于一点，此点为三角型的垂心）‎ ‎3． (2009·天津卷·理15) 在四边形中,‎ ,‎ ,‎ 则四边形的面积为 ．‎ ‎4．（2009·安徽卷·理·14）给定两个长度为1的平面向量和，它们的夹角为．如图所示，点在以为圆心的圆弧上变动．若其中,则的最大值是________．‎ ‎5．（2008，浙江9）已知a、b是平面内两个互相垂直的单位向量，若向量满足，则|c|的最大值是（ ） ‎ ‎ A．1 B．2 C． D． ‎6．（2006，四川，7）如图7.2—1，已知正六边形P1P2P3P4P5P6，下列向量的数量积中最大的是 ‎（ ）‎ A． B． C． D． ‎7．（2009，上海春，6）已知若夹角的大小为 。‎ ‎8．（2008上海，5）若向量a、b满足，且a与b的夹角为 。‎ ‎9．（2008宁夏，海南，13）已知向量，= 。‎ ‎10．（2008江苏，5）已知向量a与b的夹角为 ‎120°，=‎ ‎ 。‎ ‎11．（2008天津，14）如图，在平行四边形ABCD中，，则=‎ ‎ 。‎ ‎12．（2008，北京，10）已知向量a与b的夹角为 ‎120°且，那么的值为 。‎ ‎13．（2008陕西，15）关于平面向量a、b、c，有下列三个命题：‎ ‎①若.‎ ‎②若 ‎③非零向量a和b满足则a与a+b的夹角为60°.‎ 其中真命题的序号为 。（写出所有真命题的序号）‎ ‎14．（2007，天津，15）如图在△ABC中，∠BAC=‎ ‎120°，AB=2，AC=1，D是边BC上一点，DC、2BD，则 。‎ 高考真题答案与解析 数 学（理）‎ ‎【考点17】 平面向量的数量积及平面向量的应用 ‎1．答案：3‎ ‎【解析】考查向量的数量积（代数）运算．‎ ‎2.【解析】由知，点O到三角形ABC三顶点的距离相等，所以点O为该三角形的外心；‎ 由，所以由向量的平行四边形法则可知，向量经过三角形AB边的中点，从而NC是三角形的一条中线，同理NA，NB也是三角形的中线，故点N为三角形的重心；‎ 由，‎ 即，‎ 同理，即点P为该三角形的垂心．‎ ‎【点评】本题主要考查三角形的性质及向量运算及几何意义．‎ ‎3．答案： ‎【解析】由可知，四边形是平行四 边形，且，．‎ 由可知，的平分线与共 线，所以，四边形是菱形．则，‎ 于是由 及得，于是，进而可求出，‎ ．‎ ‎4．【解析】由图形的对称性，当在中点时取最大值2．直接求可以这样做：设 ‎ ，‎ 即 ‎∴．‎ ‎5．答案：C ‎ ‎【解析】建立平面直角坐标系，‎ 设（0，1）， 由=0得+‎ ‎ =上，又向量的起点也在圆上，且到此圆上的点的最大值等于圆的直径的大小，即 ‎ ，故选C.‎ ‎6．答案：A ‎【解析】设正六边形变长为2。‎ cos 30°=6；；‎ ；2·2cos 120°=—2。故选A。‎ ‎7．答案： ‎ 【解析】， ≤≤π。 ∴。‎ ‎8．答案： ‎ ‎【解析】∵=+2×1×2×，∴ ‎9．答案：3‎ ‎ 解析：=（4，1-，），由已知得 =，且，解得。‎ ‎10．答案：7‎ ‎ 【解析】。‎ ‎ ∴ ‎11．答案：3‎ ‎ 【解析】 ‎ （1，2）=（-1，2），∴·（1，2）=-1×1+2×2=3.‎ ‎12．答案：0‎ ‎ 【解析】×cos ‎ ‎ 120°+42=0‎ ‎13．答案：②‎ ‎ 【解析】命题①明显错误，由两向量平行的充要条 ‎ 件得1×6+2=0，，故命题②正确，由 ‎ ，再结合平行四边形法则可得 ‎ 与的夹角为30°，命题③错误。‎ ‎14．答案： ‎ 解析： 。‎ 又∵=，=2×1×cos 120°=—1，‎ ‎∴· 高考资源网(www.ks5u.com)‎ www.ks5u.com 来源：高考资源网 版权所有：高考资源网(www.k s 5 u.com)‎ 版权所有：高考资源网(www.ks5u.com)‎ 版权所有：高考资源网(www.ks5u.com)‎