圆锥曲线综合题高考常见题型与分析学生

圆锥曲线综合题高考常见题型与分析学生

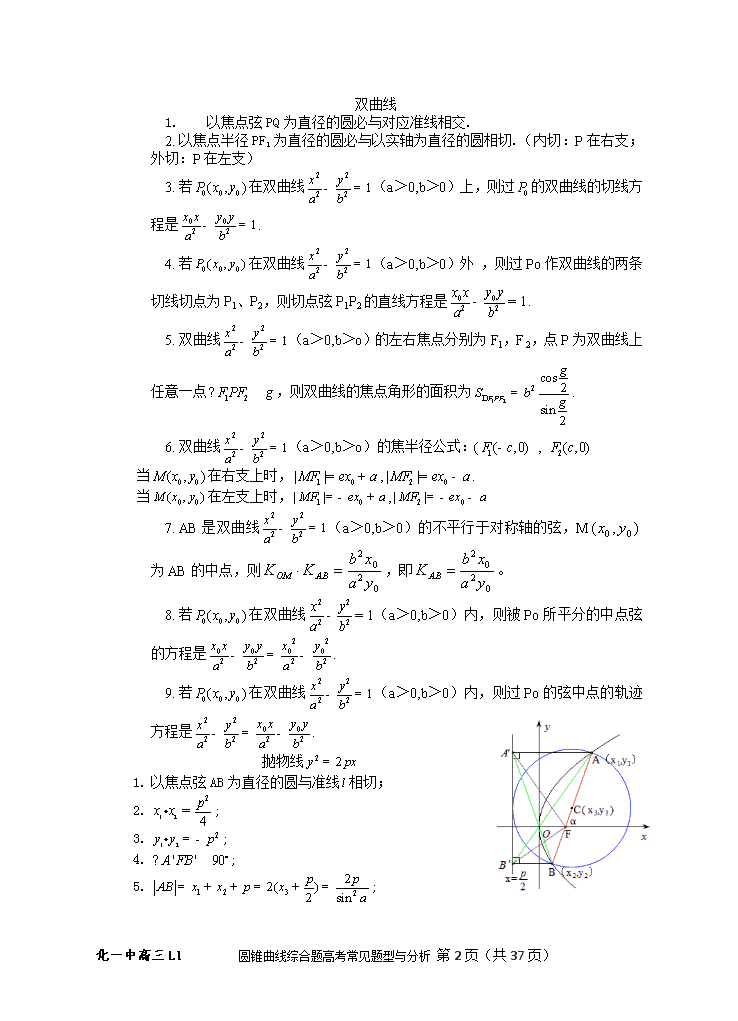
圆锥曲线综合题高考常见题型与分析 本部分重点考查直线和圆锥曲线的综合性问题,从近几年的高考试题来看,除了在解答题中必然有直线与圆锥曲线的联立外,在选择题或填空题中出现的圆锥曲线问题也经常与直线结合起来.本部分的主要特点是运算量大、思维难度较高,但有时灵活地借助几何性质来分析问题可能会收到事半功倍的效果.‎ ‎(1)关于圆锥曲线的方程求解,一般是由定义法求曲线的方程或由已知条件直接求曲线方程,有时也会以求轨迹的形式出现,难度中等.‎ ‎(2)除了方程的求解,还有如下考查内容,圆锥曲线的弦长问题、最值问题、定点定值问题、探索性问题等,考查的知识点较多,能力要求高,尤其在考查学生的运算求解变形能力上,此类问题体现的淋漓尽致,是高考试题中区分度较高的题目.‎ ‎(3)预测2015年的高考,对本节知识的考查仍以解答题为主,选择的载体一般是椭圆,主要围绕着直线与椭圆的位置关系进行命题,有时会与向量的共线、模和内积等联系起来;对于方程的求解,不要忽视轨迹的求解形式,后面的设问将是对最值、定值、定点、参数范围的考查,探索类和存在性问题考查的概率也很高.‎ 一、直线和圆锥曲线经典结论 椭 圆 1. 以焦点弦PQ为直径的圆必与对应准线相离.‎ 2. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.‎ 3. 若在椭圆上，则过的椭圆的切线方程是.‎ 4. 若在椭圆外 ，则过Po作椭圆的两条切线切点为P1、P2，则切点弦P1P2的直线方程是.‎ 5. 椭圆 (a＞b＞0)的左右焦点分别为F1，F 2，点P为椭圆上任意一点，则椭圆的焦点角形的面积为.‎ 6. 椭圆（a＞b＞0）的焦半径公式：‎ ‎,( , ).‎ 7. AB是椭圆的不平行于对称轴的弦，M为AB的中点，则，即。‎ 8. 若在椭圆内，则被Po所平分的中点弦的方程是.‎ 9. 若在椭圆内，则过Po的弦中点的轨迹方程是.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 双曲线 1. 以焦点弦PQ为直径的圆必与对应准线相交.‎ 2. 以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.（内切：P在右支；外切：P在左支）‎ 3. 若在双曲线（a＞0,b＞0）上，则过的双曲线的切线方程是.‎ 4. 若在双曲线（a＞0,b＞0）外 ，则过Po作双曲线的两条切线切点为P1、P2，则切点弦P1P2的直线方程是.‎ 5. 双曲线（a＞0,b＞o）的左右焦点分别为F1，F 2，点P为双曲线上任意一点，则双曲线的焦点角形的面积为.‎ 6. 双曲线（a＞0,b＞o）的焦半径公式：( , ‎ 当在右支上时，,.‎ 当在左支上时，,‎ 7. AB是双曲线（a＞0,b＞0）的不平行于对称轴的弦，M为AB的中点，则，即。‎ 8. 若在双曲线（a＞0,b＞0）内，则被Po所平分的中点弦的方程是.‎ 9. 若在双曲线（a＞0,b＞0）内，则过Po的弦中点的轨迹方程是.‎ 抛物线 1. 以焦点弦AB为直径的圆与准线相切；‎ 2. ‎;‎ 3. ‎;‎ 4. ‎;‎ 5. ‎;‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 1. ‎;‎ 2. A、O、三点共线；‎ 3. B、O、三点共线；‎ 4. ‎；‎ 5. ‎（定值）；‎ 6. ‎；；‎ 7. ‎；‎ 8. ‎；‎ 9. ‎;‎ 10. ‎;‎ ‎16.过抛物线上一点M(x0,y0)的切线方程为 ‎ 注意：‎ 过抛物线上一点M(x0,y0)的切线的方程为：‎ 过抛物线上一点M(x0,y0)的切线的方程为：‎ 过抛物线上一点M(x0,y0)的切线的方程为：‎ ‎17.过抛物线焦点弦的两端点的抛物线的切线的交点在准线上；过抛物线准线上任一点作抛物线的切线，则过两切点的弦必过焦点 二、2007—2014广东高考圆锥曲线综合题回顾 年份 载 体 求 解 ‎2014‎ 椭 圆 ‎（1）求椭圆标准方程；（2）求点的轨迹方程 ‎2013‎ 抛物线 ‎（1）求抛物线方程；（2）求直线方程（3）求最值 ‎2012‎ 椭 圆 ‎（1）求椭圆方程；（2）存在性问题求最值 ‎2011‎ 圆 ‎（1）求点的轨迹方程；（2）求最值 ‎2010‎ 双曲线 ‎（1）求点的轨迹方程；（2）求值 ‎2009‎ 抛物线 ‎（1）求点的轨迹方程；（2）求最值 ‎2008‎ 椭 圆 ‎（1）求椭圆方程和抛物线方程；（2）存在性问题 ‎2007‎ 椭 圆 ‎（1）求圆方程；（2）存在性问题求最值 三、圆锥曲线常考题型与解题策略 题型1：求轨迹方程 解题策略：‎ ‎（1）熟练各种圆锥曲线的有关定义、标准方程、性质；‎ ‎（2）认真审题；‎ ‎（3）列式求解；‎ ‎（4）查漏补缺下结论。‎ 特别注意：若所求的方程后面要用到，必须验算！‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 例1. （2014广东）已知椭圆的一个焦点为，离心率为。‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）若动点为椭圆外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程.‎ 变式练习：‎ ‎1.(2014辽宁) 圆的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线过点P且离心率为.‎ ‎（1）求的方程；‎ ‎（2）椭圆过点P且与有相同的焦点，直线过的右焦点且与交于A，B两点，若以线段AB为直径的圆过点P，求的方程 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎2.[2014·陕西] 如图，曲线C由上半椭圆C1：＋＝1(a>b>0，y≥0)和部分抛物线C2：y＝－x2＋1(y≤0)连接而成，C1与C2的公共点为A，B，其中C1的离心率为.‎ ‎(1)求a，b的值；‎ ‎(2)过点B的直线l与C1，C2分别交于点P，Q(均异于点A，B)，若AP⊥AQ，求直线l的方程．‎ 题型2：与圆锥曲线相关的最值问题 解题策略：(1)常用方法有配方法、判别式法、导数法、函数单调性等;‎ ‎(2)参数方程法（三角代换法）,把问题转化为三角函数问题，利用三角函数的有界性;‎ ‎(3)不等式法,通过基本不等式求最值;‎ ‎(4)数形结合法.‎ 解决最值问题一定要分清哪些量为变量,哪些量为常量;解决此类问题要综合应用多种知识,注意问题切入点的突破.‎ 例2. [2014·四川] 已知椭圆C：＋＝1(a>b>0)的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．‎ ‎(1)求椭圆C的标准方程．‎ ‎(2)设F为椭圆C的左焦点，T为直线x＝－3上任意一点，过F作TF的垂线交椭圆C于点P，Q.‎ ‎①证明：OT平分线段PQ(其中O为坐标原点)；‎ ‎②当最小时，求点T的坐标．‎ 解：(1)由已知可得解得a2＝6，b2＝2，‎ 所以椭圆C的标准方程是＋＝1.‎ ‎(2)①证法一：由(1)可得，F的坐标是(－2，0)，设T点的坐标为(－3，m)，‎ 则直线TF的斜率kTF＝＝－m.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 当m≠0时，直线PQ的斜率kPQ＝.直线PQ的方程是x＝my－2.‎ 当m＝0时，直线PQ的方程是x＝－2，也符合x＝my－2的形式．‎ 设P(x1，y1)，Q(x2，y2)，将直线PQ的方程与椭圆C的方程联立，得 得(m2＋3)y2－4my－2＝0，‎ 其判别式Δ＝16m2＋8(m2＋3)>0.所以 y1＋y2＝，y1y2＝，‎ x1＋x2＝m(y1＋y2)－4＝.‎ 设M为PQ的中点，则M点的坐标为.所以直线OM的斜率kOM＝－，‎ 又直线OT的斜率kOT＝－，所以点M在直线OT上，因此OT平分线段PQ.‎ 证法二：设T点的坐标为(－3，m)，P(x1，y1)，Q(x2，y2)，PQ中点M（x0，y0），则 若m=0，则PQ中点为F，满足OT平分线段PQ；‎ 若，则 由，得O,M,T花线 综上：OT平分线段PQ。‎ ‎② 方一：由①可得，|TF|＝，‎ ‎|PQ|＝＝ ‎＝＝.‎ 所以＝＝ ‎≥＝.‎ 当且仅当m2＋1＝，即m＝±1时，等号成立，此时取得最小值．‎ 故当最小时，T点的坐标是(－3，1)或(－3，－1)．‎ 方二：由（1），得是椭圆的左准线，离心，由①及椭圆第二定义，得 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎，‎ 余略。‎ 变式练习：‎ ‎3.[2014·浙江卷] 如图，设椭圆C：＋＝1(a>b>0)，动直线l与椭圆C只有一个公共点P，且点P在第一象限．‎ ‎(1)已知直线l的斜率为k，用a，b，k表示点P的坐标；‎ ‎(2)若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a－b.‎ ‎4.[2014·山东卷] 已知抛物线C：y2＝2px(p＞0)的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|＝|FD|.当点A的横坐标为3时，△ADF为正三角形．‎ ‎(1)求C的方程．‎ ‎(2)若直线l1∥l，且l1和C有且只有一个公共点E.‎ ‎①证明直线AE过定点，并求出定点坐标．‎ ‎②△ABE的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 题型3：与圆锥曲线相关的存在性问题 求解策略： (1)思路:先假设存在,推证满足条件的结论,若结论正确则存在;若结论不正确则不存在.‎ ‎(2)策略:①当条件和结论不唯一时要分类讨论;‎ ‎②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;‎ ‎③当条件和结论都不知,按常规法解题很难时,可先由特殊情况探究,再推广到一般情况.‎ 例3.(2014深圳一模) 如图，直线，抛物线，已知点在抛物线上，且抛物线上的点到直线的距离的最小值为．‎ ‎（1）求直线及抛物线的方程；‎ ‎（2）过点的任一直线（不经过点）与抛物线交于、两点，直线与直线相交于点，记直线，，的斜率分别为，， ．问：是否存在实数，使得？若存在，试求出的值；若不存在，请说明理由．‎ 解：（1）（法一）点在抛物线上， ． ‎ 设与直线平行且与抛物线相切的直线方程为，‎ 由 得， ‎ ‎，‎ 由，得，则直线方程为．‎ 两直线、间的距离即为抛物线上的点到直线的最短距离，‎ 有，解得或（舍去）．‎ 直线的方程为，抛物线的方程为． ‎ ‎（法二）点在抛物线上， ‎ ‎，抛物线的方程为． ‎ 设为抛物线上的任意一点，点到直线的距离为，‎ 根据图象，有，‎ ‎，‎ ‎，的最小值为，由，解得 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎．‎ 因此，直线的方程为，抛物线的方程为． ‎ ‎（2）直线的斜率存在，‎ 设直线的方程为，即，‎ 由 得，‎ 设点、的坐标分别为、，则，，‎ ‎，， ‎ 由 得，，‎ ‎， ．‎ 因此，存在实数，使得成立，且．‎ 点评:(1)常常根据题意建立含有参数的等式或不等式,通过解等式或不等式求参数的值或范围.(2)建立关于某变量的一元二次方程,利用根与系数的关系或利用判别式求参数或参数的范围.‎ 变式练习：‎ ‎5.已知动圆P与圆F1:(x+3)2+y2=81相切,且与圆F2:(x-3)2+y2=1相内切,记圆心P的轨迹为曲线C;设Q为曲线C上的一个不在x轴上的动点,O为坐标原点,过点F2作OQ的平行线交曲线C于两个不同的点M,N.‎ ‎(1)求曲线C的方程;‎ ‎(2)试探究|MN|和|OQ|2的比值能否为一个常数?若能,求出这个常数;若不能,请说明理由;‎ ‎(3)记△QF2M的面积为S1,△OF2N的面积为S2,令S=S1+S2,求S的最大值.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎6. 在平面直角坐标系xOy中,经过点(0,‎2‎)且斜率为k的直线l与椭圆x‎2‎‎2‎+y2=1有两个不同的交点P和Q.‎ ‎(1)求k的取值范围;‎ ‎(2)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量OP‎+OQ与AB共线?如果存在,求出k的值;如果不存在,请说明理由.‎ ‎7.[2014·邯郸期末] 已知点F1(－1，0)，F2(1，0)分别是椭圆C：＋＝1(a>b>0)的左、右焦点，点P在椭圆C上．‎ ‎(1)求椭圆C的标准方程．‎ ‎(2)设直线l1：y＝kx＋m，l2：y＝kx－m，若l1，l2均与椭圆C相切，试探究在x轴上是否存在定点M，点M到l1，l2的距离之积恒为1.若存在，请求出点M的坐标；若不存在，请说明理由．‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 题型4：与圆锥曲线的弦长、距离、面积等有关的问题 解题策略：‎ ‎（1）当直线的斜率是否存在未定时，用点斜式或斜截式表示直线时，需分类讨论；当直线与y轴不垂直时，可设直线为的形式。将直线方程与圆锥曲线方程联立,构成方程组,得到型如的方程，判别式为△，利用根与系数的关系设而不求计算弦长,设两交点为，则|AB|==（k为直线AB的斜率）；‎ ‎（2）当涉及过焦点的弦长问题时,可考虑用圆锥曲线的定义；‎ ‎（3）当弦过原点时，可考虑转化为极坐标方程解。‎ 例4． (2014大纲全国,理21)已知抛物线C:y2=2px(p>0)的焦点为F，直线y=4与y轴的交点为P,与C的交点为Q,且|QF|=|PQ|.‎ ‎(1)求C的方程;‎ ‎(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线l'与C相交于M、N两点，且A、M、B、N四点在同一圆上,求l的方程.‎ 命题定位:本题主要考查抛物线的定义、直线方程、一元二次方程的根与系数的关系、弦长公式等知识,体现数形结合的思想、函数方程思想.对运算求解能力、分析问题和解决问题的能力、数学探究能力及综合运用知识的能力有较高的要求. ‎ 解：（I）设，代入，得 由题设得，解得（舍去）或，‎ ‎∴C的方程为；‎ ‎（II）由题设知与坐标轴不垂直，故可设的方程为，‎ 代入，得．‎ 设则．‎ 故的中点为 又的斜率为 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 的方程为．‎ 将上式代入，并整理得．‎ 设则 ‎．‎ 故的中点为 ‎．‎ 由垂直平分，故四点在同一圆上等价于，则 ‎ ‎ 即，‎ 化简得，解得或．‎ 所求直线的方程为或．‎ 变式练习：‎ ‎8.(2014课标全国Ⅰ) 已知点（0，-2），椭圆：的离心率为，是椭圆的焦点，直线的斜率为，为坐标原点.‎ ‎(Ⅰ)求的方程；‎ ‎（Ⅱ）设过点的直线与相交于两点，当的面积最大时，求的方程.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎9. 在平面直角坐标系xOy中，过定点C（0，p）作直线与抛物线x2=2py（p>0）相交于A、B两点。‎ ‎（Ⅰ）若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值；‎ ‎（Ⅱ）是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得弦长恒为定值？若存在，求出l的方程；若不存在，说明理由。‎ 题型5：圆锥曲线的中点弦问题 解题策略：这类问题一般有以下三种类型：‎ ‎（1）求中点弦所在直线方程问题；‎ ‎（2）求弦中点的轨迹方程问题；‎ ‎（3）求弦中点的坐标问题。‎ 其解法有“点差法”、设而不求法、参数法、待定系数法及中心对称变换法等。‎ 例5.[2014·湖南] 如图7，为坐标原点，椭圆的左右焦点分别为，离心率为；双曲线的左右焦点分别为，离心率为，已知，且. ‎ ‎（Ⅰ）求的方程；‎ 图7‎ ‎（Ⅱ）过作的不垂直于轴的弦，为的中点，当直线与交于两点时，求四边形面积的最小值.‎ 解：（Ⅰ），‎ 即，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 从而，‎ 于是，‎ ‎，‎ 故椭圆方程为,双曲线的方程为.‎ ‎（Ⅱ）因为直线不垂直于轴且过点，故设直线的方程为. ‎ 由得，‎ 设，则是上述方程的两个实根，‎ 因此，的中点为，‎ 故直线的斜率为，的方程为，即.‎ 由得，‎ 设点到直线的距离为，则点到直线的距离也为，‎ 因为点在直线的异侧，所以，‎ 于是,‎ 从而 又因为，所以 四边形面积 而，故当时，取得最小值2.‎ 故四边形面积的最小值为2.‎ 变式练习：‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎10.（2013新课标Ⅱ）平面直角坐标系xoy中,过椭圆 的右焦点作直交于A,B两点,为的中点,且OP的斜率为.‎ ‎(Ⅰ)求的方程;‎ ‎(Ⅱ)为上的两点,若四边形的对角线,求四边形面积的最大值.‎ ‎11. 已知椭圆过点，且离心率。‎ ‎ （Ⅰ）求椭圆方程；‎ ‎ （Ⅱ）若直线与椭圆交于不同的两点、，且线段的垂直平分线过定点，求的取值范围。‎ 题型6：圆锥曲线中的参数问题 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 解题策略：(1)函数法,用其他变量表示该参数,建立函数关系,利用函数值域来求解;‎ ‎(2)不等式法,根据题意建立含有参数的不等式,通过解不等式求参数的范围;‎ ‎(3)判别式法,建立关于某变量的一元二次方程,利用判别式Δ≥0求参数的范围;‎ ‎(4)方程思想,建立含有参数的等式,通过等式确定参数.‎ 例6.[2014·佛山质检] 已知椭圆C的左、右焦点分别为F1(－1，0)，F2(1，0)，且F2到直线x－y－9＝0的距离等于椭圆的短轴长．‎ ‎(1)求椭圆C的方程；‎ ‎(2)若圆P的圆心为P(0，t)(t>0)，且经过F1，F2，Q是椭圆C上的动点且在圆P外，过点Q作圆P的切线，切点为M，当|QM|的最大值为时，求t的值．‎ 解：(1)设椭圆的方程为＋＝1(a>b>0)．‎ 依题意可知，2b＝＝4，所以b＝2.‎ 又c＝1，故a2＝b2＋c2＝5，‎ 故椭圆C的方程为＋＝1.‎ ‎(2)设Q(x0，y0)，圆P的方程为x2＋(y－t)2＝t2＋1.‎ 因为PM⊥QM，所以 ‎|QM|＝＝＝.‎ 若－4t≤－2，即t≥，当y0＝－2时，|QM|取得最大值，‎ ‎|QM|max＝＝，解得t＝<(舍去)．‎ 若－4t>－2，即0b>0)的左、右焦点分别为F1，F2，右顶点为A，上顶点为B.已知|AB|＝|F1F2|.‎ ‎(1)求椭圆的离心率；‎ ‎(2)设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过原点O的直线l与该圆相切，求直线l的斜率．‎ 解：(1)设椭圆右焦点F2的坐标为(c，0)．‎ 由|AB|＝|F1F2|，可得a2＋b2＝3c2.‎ 又b2＝a2－c2，则＝，‎ 所以椭圆的离心率e＝.‎ ‎(2)由(1)知a2＝2c2，b2＝c2.故椭圆方程为＋＝1.‎ 设P(x0，y0)．由F1(－c，0)，B(0，c)，有＝(x0＋c，y0)，＝(c，c)．‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 由已知，有·＝0，即(x0＋c)c＋y0c＝0.‎ 又c≠0，故有x0＋y0＋c＝0.①‎ 又因为点P在椭圆上，所以＋＝1.②‎ 由①和②可得3x＋4cx0＝0.‎ 而点P不是椭圆的顶点，故x0＝－c.‎ 代入①得y0＝，即点P的坐标为.‎ 设圆的圆心为T(x1，y1)，则x1＝＝－c，y1＝＝c，‎ 则圆的半径r＝＝c.‎ 设直线l的斜率为k，依题意，直线l的方程为y＝kx.‎ 由l与圆相切，可得＝r，即＝c，‎ 整理得k2－8k＋1＝0，解得k＝4±，‎ 所以直线l的斜率为4＋或4－.‎ 变式练习：‎ ‎ 16.[2014·重庆卷] 如图所示，设椭圆＋＝1(a>b>0)的左、右焦点分别为F1，F2，点D在椭圆上，DF1⊥F1F2，＝2，△DF1F2的面积为.‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设圆心在y轴上的圆与椭圆在x轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎17.[2014·新课标全国卷Ⅱ] 设F1，F2分别是椭圆C：＋＝1(a＞b＞0)的左、右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N.‎ ‎(1)若直线MN的斜率为，求C的离心率；‎ ‎(2)若直线MN在y轴上的截距为2，且|MN|＝5|F1N|，求a，b.‎ ‎18.[2014·安徽] 如图，已知两条抛物线E1：y2＝2p1x(p1＞0)和E2：y2＝2p2x ‎(p2＞0)，过原点O的两条直线l1和l2，l1与E1，E2分别交于A1，A2两点，l2与E1，E2分别交于B1，B2两点．‎ ‎ (1)证明：A1B1∥A2B2；‎ ‎(2)过O作直线l(异于l1，l2)与E1，E2分别交于C1，C2两点，记△A1B1C1与△A2B2C2的面积分别为S1与S2，求的值．‎ ‎ ‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 变式练习参考答案 ‎1．解：（1）‎ ‎（2）由（1）可知双曲线C1的焦点（±，0），即为椭圆C2的焦点．‎ 可设椭圆C2的方程为（b1＞0）．‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 把P代入可得，解得=3，‎ 因此椭圆C2的方程为．‎ 由题意可设直线l的方程为x=my+，A（x1，y1），B（x2，y2），‎ 联立，化为，‎ ‎∴，．‎ ‎∴x1+x2==，‎ x1x2==．‎ ‎，，‎ ‎∵，∴，‎ ‎∴+，‎ ‎∴，解得m=或m=，‎ 因此直线l的方程为：或． ‎ ‎2.解：(1) ‎ ‎ （2），‎ ‎：‎ ‎，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 方法二：若设直线l的方程为x＝my＋1(m≠0)，比照方法一给分．‎ ‎3. 解：(1)设直线l的方程为y＝kx＋m(k<0，m>0)，‎ 由得(b2＋a2k2)x2＋2a2kmx＋a2m2－a2b2＝0.‎ 由于l与C只有一个公共点，故Δ＝0，即b2－m2＋a2k2＝0，‎ 解得点P的坐标为.‎ 又点P在第一象限，故点P的坐标为P.‎ ‎(2)由于直线l1过原点O且与l垂直，故直线l1的方程为x＋ky＝0，所以 点P到直线l1的距离d＝，‎ 整理得d＝.‎ 因为a2k2＋≥2ab，所以≤＝a－b，‎ 当且仅当k2＝时等号成立．‎ 所以，点P到直线l1的距离的最大值为a－b.‎ ‎4. 解：(1)由题意知F.设D(t，0)(t>0)，则FD的中点为.‎ 因为|FA|＝|FD|，由抛物线的定义知3＋＝，‎ 解得t＝3＋p或t＝－3(舍去)．‎ 由＝3，解得p＝2，‎ 所以抛物线C的方程为y2＝4x.‎ ‎(2)①证明：由(1)知F(1，0)．设A(x0，y0)(x0y0≠0)，D(xD，0)(xD>0)．‎ 因为|FA|＝|FD|，则|xD－1|＝x0＋1，‎ 由xD>0得xD＝x0＋2，故D(x0＋2，0)．故直线AB的斜率kAB＝－.‎ 因为直线l1和直线AB平行，设直线l1的方程为y＝－x＋b，‎ 代入抛物线方程得y2＋y－＝0，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 由题意Δ＝＋＝0，得b＝－.‎ 设E(xE，yE)，则yE＝－，xE＝.‎ 当y≠4时，kAE＝＝－＝，‎ 可得直线AE的方程为y－y0＝(x－x0)，‎ 由y＝4x0，整理可得y＝(x－1)，直线AE恒过点F(1，0)．‎ 当y＝4时，直线AE的方程为x＝1，过点F(1，0)．‎ 所以直线AE过定点F(1，0)．‎ ‎②由①知，直线AE过焦点F(1，0)，‎ 所以|AE|＝|AF|＋|FE|＝(x0＋1)＋＝x0＋＋2.‎ 设直线AE的方程为x＝my＋1，因为点A(x0，y0)在直线AE上，故m＝.‎ 设B(x1，y1)．直线AB的方程为y－y0＝－(x－x0)，‎ 由y0≠0，得x＝－y＋2＋x0.代入抛物线方程得y2＋y－8－4x0＝0，所以y0＋y1＝－，‎ 可求得y1＝－y0－，x1＝＋x0＋4.‎ 所以点B到直线AE的距离为 d＝＝＝4，‎ 则△ABE的面积S＝×4x0＋＋2≥16，‎ 当且仅当＝x0，即x0＝1时，等号成立．‎ 所以△ABE的面积的最小值为16.‎ ‎5. 解:(1)设圆心P的坐标为(x,y),半径为R,‎ ‎∵动圆P与圆F1:(x+3)2+y2=81相切,且与圆F2:(x-3)2+y2=1相内切,‎ ‎∴动圆P与圆F1:(x+3)2+y2=81只能内切.‎ ‎∴‎|PF‎1‎|=9-R‎|PF‎2‎|=R-1‎⇒|PF1|+|PF2|=8>|F1F2|=6.‎ ‎∴圆心P的轨迹为以F1,F2为焦点的椭圆,其中2a=8,2c=6.‎ ‎∴a=4,c=3,b2=a2-c2=7.‎ 故曲线C的方程为x‎2‎‎16‎‎+‎y‎2‎‎7‎=1.‎ ‎(2)设M(x1,y1),N(x2,y2),Q(x3,y3),直线OQ的方程为x=my,则直线MN的方程为x=my+3.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 由x=my,‎x‎2‎‎16‎‎+y‎2‎‎7‎=1,‎可得x‎2‎‎=‎112‎m‎2‎‎7m‎2‎+16‎,‎y‎2‎‎=‎112‎‎7m‎2‎+16‎,‎则x‎3‎‎2‎‎=‎112‎m‎2‎‎7m‎2‎+16‎,‎y‎3‎‎2‎‎=‎112‎‎7m‎2‎+16‎.‎ ‎∴|OQ|2=x‎3‎‎2‎‎+‎y‎3‎‎2‎=‎112‎m‎2‎‎7m‎2‎+16‎‎+‎112‎‎7m‎2‎+16‎=‎‎112(m‎2‎+1)‎‎7m‎2‎+16‎.‎ 由x=my+3,‎x‎2‎‎16‎‎+y‎2‎‎7‎=1,‎可得(7m2+16)y2+42my-49=0,∴y1+y2=-‎42m‎7m‎2‎+16‎,y1y2=-‎49‎‎7m‎2‎+16‎.‎ ‎∴|MN|=‎(x‎2‎-x‎1‎‎)‎‎2‎+(y‎2‎-‎y‎1‎‎)‎‎2‎=‎‎[(my‎2‎+3)-(my‎1‎+3)]‎‎2‎‎+(y‎2‎-‎y‎1‎‎)‎‎2‎ ‎=m‎2‎‎+1‎|y2-y1|=m‎2‎‎+1‎‎(y‎1‎+y‎2‎‎)‎‎2‎-4‎y‎1‎y‎2‎=m‎2‎‎+1‎‎-‎‎42m‎7m‎2‎+16‎‎2‎‎-4‎‎-‎‎49‎‎7m‎2‎+16‎=‎56(m‎2‎+1)‎‎7m‎2‎+16‎.‎ ‎∴‎|MN|‎‎|OQ‎|‎‎2‎‎=‎56(m‎2‎+1)‎‎7m‎2‎+16‎‎112(m‎2‎+1)‎‎7m‎2‎+16‎=‎‎1‎‎2‎.‎ ‎∴|MN|和|OQ|2的比值为一个常数,这个常数为‎1‎‎2‎.‎ ‎(3)∵MN∥OQ,∴△QF2M的面积=△OF2M的面积.‎ ‎∴S=S1+S2=S△OMN.‎ ‎∵O到直线MN:x=my+3的距离d=‎3‎m‎2‎‎+1‎,‎ ‎∴S=‎1‎‎2‎|MN|·d=‎‎1‎‎2‎‎×‎56(m‎2‎+1)‎‎7m‎2‎+16‎×‎3‎m‎2‎‎+1‎=‎84‎m‎2‎‎+1‎‎7m‎2‎+16‎=‎84‎m‎2‎‎+1‎‎7m‎2‎‎+1‎‎2‎+9‎=‎84‎‎7m‎2‎‎+1‎+‎‎9‎m‎2‎‎+1‎≤‎84‎‎2‎‎7×9‎=2‎‎7‎ 当且仅当‎7m‎2‎‎+1‎=‎‎9‎m‎2‎‎+1‎即m=±‎14‎‎7‎时,S取最大值2‎7‎.‎ ‎(或：令m‎2‎‎+1‎=t,则m2=t2-1(t≥1),S=‎84t‎7(t‎2‎-1)+16‎‎=‎84t‎7t‎2‎+9‎=‎‎84‎‎7t+‎‎9‎t.‎ ‎∵7t+‎9‎t≥2‎7t·‎‎9‎t=6‎7‎(当且仅当7t=‎9‎t,‎ 即t=‎3‎‎7‎,亦即m=±‎14‎‎7‎时取等号),∴当m=±‎14‎‎7‎时,S取最大值2‎7‎.）‎ ‎6. 解:(1)由已知条件知直线l的方程为y=kx+‎2‎,‎ 代入椭圆方程,得x‎2‎‎2‎+(kx+‎2‎)2=1,整理得‎1‎‎2‎‎+‎k‎2‎x2+2‎2‎kx+1=0.①‎ 由直线l与椭圆有两个不同的交点P和Q,‎ 得Δ=8k2-4‎1‎‎2‎‎+‎k‎2‎=4k2-2>0,解得k<-‎2‎‎2‎或k>‎2‎‎2‎.‎ 故k的取值范围为‎-∞,-‎‎2‎‎2‎‎∪‎‎2‎‎2‎‎,+∞‎.‎ ‎(2)设P(x1,y1),Q(x2,y2),则OP‎+‎OQ=(x1+x2,y1+y2).‎ 由方程①,知x1+x2=-‎4‎2‎k‎1+2‎k‎2‎.②‎ 又y1+y2=k(x1+x2)+2‎2‎‎=‎‎2‎‎2‎‎1+2‎k‎2‎.③‎ 由A(‎2‎,0),B(0,1),得AB=(-‎2‎,1).所以OP‎+OQ与AB共线等价于x1+x2=-‎2‎(y1+y2),‎ 将②③代入,解得k=‎2‎‎2‎.‎ 因为由(1)知k<-‎2‎‎2‎或k>‎2‎‎2‎,所以不存在符合题意的常数k.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎7. 解：(1)方法一：由F1(－1，0)，F2(1，0)是椭圆的两个焦点，得c＝1.‎ 又∴a2＝2，b2＝1，故椭圆C的方程为＋y2＝1.‎ 方法二：由F1(－1，0)，F2(1，0)是椭圆的两个焦点，得c＝1.‎ 又2a＝|PF1|＋|PF2|＝＋＝2 ，‎ ‎∴a＝，∴b＝1. 故椭圆C的方程为＋y2＝1.‎ ‎(2)把l1的方程代入椭圆方程，整理得(1＋2k2)x2＋4mkx＋2m2－2＝0.‎ ‎∵直线l1与椭圆C相切，‎ ‎∴Δ＝16k2m2－4(1＋2k2)(2m2－2)＝0，化简得m2＝1＋2k2.‎ 同理把l2的方程代入椭圆方程，也得m2＝1＋2k2.‎ 设在x轴上存在点M(t，0)，点M到直线l1，l2的距离之积为1，则 ·＝1，即|k2t2－m2|＝k2＋1，‎ 把1＋2k2＝m2代入上式并去绝对值整理，得k2(t2－3)＝2或k2(t2－1)＝0.‎ k2(t2－3)＝2显然不恒成立，‎ 要使得k2(t2－1)＝0对任意的k∈R恒成立，则t2－1＝0，解得t＝±1.‎ 综上所述，满足题意的定点M存在，其坐标为(－1，0)或(1，0)．‎ ‎8. 解：(Ⅰ) 设，由条件知，得= ‎ 又，所以a=2=， ,故的方程. ‎ ‎（Ⅱ）依题意当轴不合题意，故设直线l：，设 ‎ 将代入，得，‎ 当，即时，‎ 从而= + 又点O到直线PQ的距离，所以OPQ的面积 ‎ ，‎ 当且仅当，即等号成立，且满足，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎（或：设，则，，当且仅当，等号成立，且满足）‎ 所以当OPQ的面积最大时，的方程为： 或. ‎ ‎9. （Ⅰ）依题意，点N的坐标为N（0,-p）,可设A（x1,y1）,B（x2,y2），直线AB的方程为y=kx+p,与x2=2py联立得x2-2pkx-2p2=0.‎ 由韦达定理得x1+x2=2pk，x1x2=-2p2.‎ 于是＝‎ ‎＝‎ ‎.‎ ‎（Ⅱ）假设满足条件的直线l存在，其方程为y=a,AC的中点为径的圆相交于点P、Q，PQ的中点为H，则 ‎＝.‎ ‎=＝‎ ‎=‎ 令，得为定值，故满足条件的直线l存在，其方程为，即抛物线的通径所在的直线.‎ 解法2：（Ⅰ）前同解法1，再由弦长公式得 ‎＝‎ 又由点到直线的距离公式得.‎ 从而，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ ‎（Ⅱ）假设满足条件的直线t存在，其方程为y=a，则以AC为直径的圆的为 将直线方程y=a代入得 设直线l与以AC为直径的圆的交点为P（x2,y2）,Q（x4,y4）,则有 令为定值 故满足条件的直线l存在，其方程为.即抛物线的通径所在的直线。‎ ‎10. 解：(1)设A(x1，y1)，B(x2，y2)，P(x0，y0)，则 ‎，，，‎ 由此可得.‎ 因为x1＋x2＝2x0，y1＋y2＝2y0，，所以a2＝2b2.‎ 又由题意知，M的右焦点为(，0)，故a2－b2＝3.因此a2＝6，b2＝3.‎ 所以M的方程为.‎ ‎(2)由解得或因此|AB|＝.‎ 由题意可设直线CD的方程为y＝，‎ 设C(x3，y3)，D(x4，y4)．‎ 由得3x2＋4nx＋2n2－6＝0.于是x3,4＝.‎ 因为直线CD的斜率为1，所以|CD|＝.‎ 由已知，四边形ACBD的面积.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 当n＝0时，S取得最大值，最大值为.‎ 所以四边形ACBD面积的最大值为.‎ ‎11. 解：（Ⅰ）离心率，，即 ①；‎ 又椭圆过点，则，‎ ①式代入上式，解得，，‎ 故椭圆方程为。‎ ‎（Ⅱ）解法一：设，弦MN的中点A 由得：，‎ 直线与椭圆交于不同的两点，‎ ‎，即 ②‎ 由韦达定理得：，‎ 则，‎ 直线AG的斜率为：，‎ 由直线AG和直线MN垂直可得：，即，‎ 代入②式，可得，即，则。‎ 解法二：设，弦MN的中点A，则 两式相减，得 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 当时，由得 由题意，得A在直线和椭圆内且不在x轴上，则或，在此范围单调递增，故 或。‎ ‎12. 解：(1)设点M(x，y)，依题意得|MF|＝|x|＋1，即＝|x|＋1，‎ 化简整理得y2＝2(|x|＋x)．‎ 故点M的轨迹C的方程为y2＝ ‎(2)在点M的轨迹C中，记C1：y2＝4x，C2：y＝0(x<0)．‎ 依题意，可设直线l的方程为y－1＝k(x＋2)．‎ 由方程组可得ky2－4y＋4(2k＋1)＝0.①‎ 当k＝0时，y＝1.把y＝1代入轨迹C的方程，得x＝.‎ 故此时直线l：y＝1与轨迹C恰好有一个公共点.‎ 当k≠0时，方程①的判别式Δ＝－16(2k2＋k－1)．②‎ 设直线l与x轴的交点为(x0，0)，则由y－1＝k(x＋2)，‎ 令y＝0，得x0＝－.③‎ ‎(i)若由②③解得k<－1或k>.‎ 即当k∈(－∞，－1)∪时，直线l与C1没有公共点，与C2有一个公共点．故此时直线l与轨迹C恰好有一个公共点．‎ ‎(ii)若或 由②③解得k∈或－≤k<0.即当k∈时，直线l与C1只有一个公共点．‎ 当k∈时，直线l与C1有两个公共点，与C2没有公共点．‎ 故当k∈∪时，直线l与轨迹C恰好有两个公共点．‎ ‎(iii)若由②③解得－10，y2>0，F1P1，F2P2是圆C的切线，且F1P1⊥F2P2.由圆和椭圆的对称性，易知，x2＝－x1，y1＝y2，|P1P2|＝2|x1|.‎ 由(1)知F1(－1，0)，F2(1，0)，所以＝(x1＋1，y1)，＝(－x1－1，y1)．‎ 再由F1P1⊥F2P2得－(x1＋1)2＋y＝0.‎ 由椭圆方程得1－＝(x1＋1)2，即3x＋4x1＝0，‎ 解得x1＝－或x1＝0.‎ 当x1＝0时，P1，P2重合，此时题设要求的圆不存在．‎ 当x1＝－时，过P1，P2分别与F1P1，F2P2垂直的直线的交点即为圆心C.由F1P1，F2P2是圆C的切线，且F1P1⊥F2P2，知CP1⊥CP2.‎ 又|CP1|＝|CP2|，故圆C的半径|CP1|＝|P1P2|＝|x1|＝.‎ ‎17. 解：(1)根据c＝及题设知M，2b2＝3ac.‎ 将b2＝a2－c2代入2b2＝3ac，解得＝，＝－2(舍去)．‎ 故C的离心率为.‎ ‎(2)由题意知，原点O为F1F2的中点，MF2∥y轴，所以直线MF1与y轴的交点D(0，2)是线段MF1的中点，故＝4，即b2＝4a.①‎ 由|MN|＝5|F1N|，得|DF1|＝2|F1N|.设N(x1，y1)，由题意知y1<0，则 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 即代入C的方程，得＋＝1.②‎ 将①及c＝代入②得＋＝1，‎ 解得a＝7，b2＝4a＝28，故a＝7，b＝2.‎ ‎18. (1)证明：设直线l1，l2的方程分别为y＝k1x，y＝k2x(k1，k2≠0)，‎ 则由 得A1，‎ 由得A2.‎ 同理可得B1，B2.‎ 所以＝＝2p1，‎ ＝＝2p2.‎ 故＝，所以A1B1∥A2B2‎ ‎(2) 解：由(1)知A1B1∥A2B2，同理可得B1C1∥B2C2，C1A1∥C2A2，‎ 所以△A1B1C1∽△A2B2C2，因此＝.‎ 又由(1)中的＝||知，＝，故＝.‎ ‎19. 解法一：（Ⅰ）设点，则，由得：‎ ‎，‎ 化简得.‎ ‎（Ⅱ）设直线的方程为.设，，又，‎ 联立方程组，消去得：，，‎ 故，‎ 由，得：‎ ‎，，整理得：，，‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎ 解法二：（Ⅰ）由得：，‎ ‎，，‎ 所以点的轨迹是抛物线，由题意，轨迹的方程为：.‎ ‎（Ⅱ）由已知，，得.则：‎ ‎.…………①‎ 过点分别作准线的垂线，垂足分别为，，‎ 则有：.…………②，‎ 由①②得：，即.‎ 化一中高三L1 圆锥曲线综合题高考常见题型与分析 第37页（共37页）‎