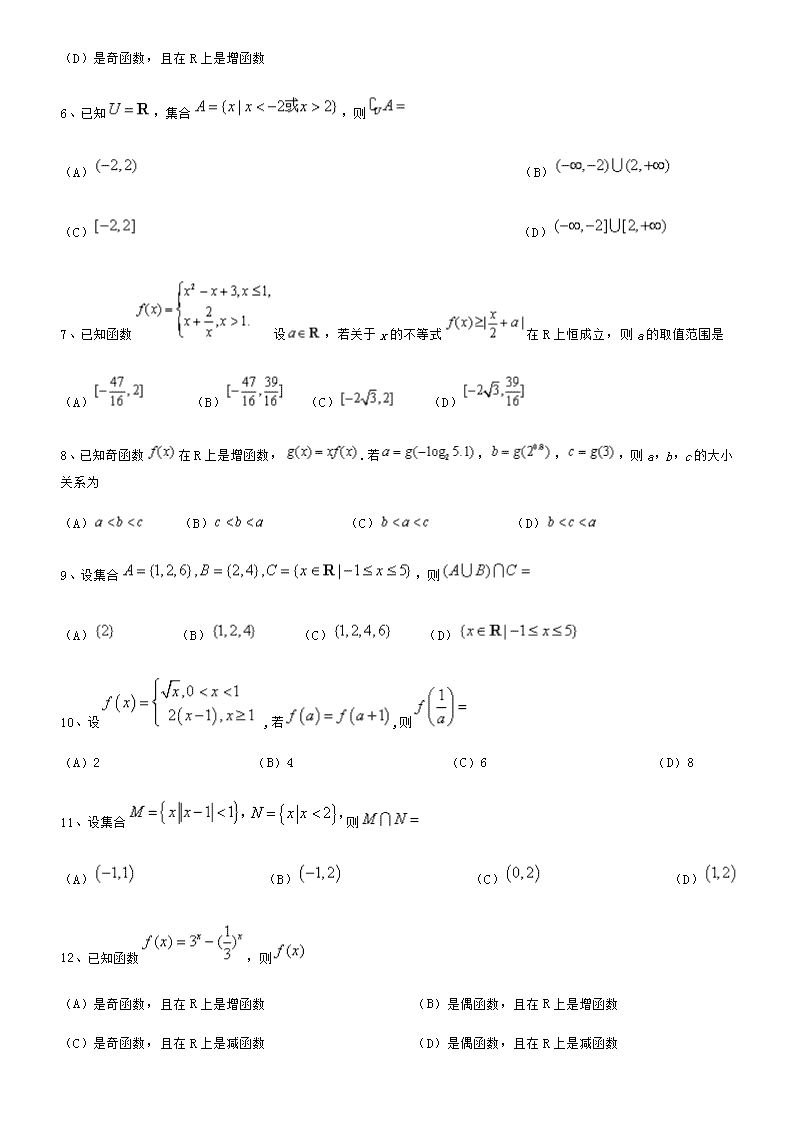数学必修一练习——精选高考题
2018年数学必修一练习——精选高考题
每个高中生都有一个共同的目标——高考,每一次考试都在为高考蓄力,考向,要求也与高考一致。本练习全部来源于2016、2017年高考真题,无论是备战期末考还是寒假提升,都是能力的拔高。
一、选择题
1、已知函数设,若关于的不等式在上恒成立,则的取值范围是
(A)(B)(C)(D)
2、已知奇函数在上是增函数.若,则的大小关系为
(A)(B)(C)(D)
3、设集合,则
(A)(B)(C)(D)
4、根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是
(参考数据:lg3≈0.48)
(A)1033 (B)1053
(C)1073 (D)1093
5、已知函数,则
(A)是偶函数,且在R上是增函数
(B)是奇函数,且在R上是增函数
(C)是偶函数,且在R上是减函数
(D)是奇函数,且在R上是增函数
6、已知,集合,则
(A) (B)
(C) (D)
7、已知函数设,若关于x的不等式在R上恒成立,则a的取值范围是
(A) (B) (C) (D)
8、已知奇函数在R上是增函数,.若,,,则a,b,c的大小关系为
(A) (B) (C) (D)
9、设集合,则
(A) (B) (C) (D)
10、设,若,则
(A)2 (B)4 (C)6 (D)8
11、设集合则
(A) (B) (C) (D)
12、已知函数,则
(A)是奇函数,且在R上是增函数 (B)是偶函数,且在R上是增函数
(C)是奇函数,且在R上是减函数 (D)是偶函数,且在R上是减函数
13、已知集合 则
A.[2,3] B.( -2,3 ] C.[1,2) D.
14、 已知函数满足:且.( )
A.若,则 B.若,则
C.若,则 D.若,则
15、已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则=( )
A.{1} B.{3,5} C.{1,2,4,6} D.{1,2,3,4,5}
16、某公司为激励创新,计划逐年加大研发奖金投入。若该公司2015年全年投入研发奖金130万元,在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是
(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30)
(A)2018年 (B) 2019年 (C)2020年 (D)2021年
17、设集合A={x11≤x≤5},Z为整数集,则集合A∩Z中元素的个数是
(A)6 (B) 5 (C)4 (D)3
二、填空题
18、已知,,且x+y=1,则的取值范围是__________.
19、已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当时,,则f(919)= .
20、已知函数是定义在R上的奇函数,当x时,,
则
21、已知点在函数的图像上,则
22、设,则不等式的解集为_______.
23、.设函数f(x)=x3+3x2+1.已知a≠0,且f(x)–f(a)=(x–b)(x–a)2,x∈R,则实数a=_____,b=______.
24、已知函数在R上单调递减,且关于x的方程恰有两个不相等的实数解,则的取值范围是_________.
25、若函数f(x)是定义R上的周期为2的奇函数,当0
1;
(2)若关于的方程+=0的解集中恰有一个元素,求的值;
(3)设>0,若对任意,函数在区间上的最大值与最小值的差不超过1,求的取值范围.
29、已知函数.
(1) 设a=2,b=.
① 求方程=2的根;
② 若对任意,不等式恒成立,求实数m的最大值;
(2)若,函数有且只有1个零点,求ab的值。
高一资料介绍
高一上期中考部分
1.2017—2018学年高一第一学期期中质量检测(物理)
2.2017—2018学年高一第一学期期中质量检测(语文)
3.2017—2018学年高一第一学期期中质量检测(数学)两份
4.2017—2018学年高一第一学期期中质量检测(化学)
物理部分
1. 高一物理运动学综合练习--基础
2. 高一物理运动学综合练习--提升
3. 高一物理牛顿定律综合练习--基础
4. 高一物理牛顿定律综合练习--提升
数学部分
1.2018年数学必修二专项练习
2.2018年数学必修三专项练习
3.2018年数学必修四专项练习
4.2018年数学必修一能力提高卷
5.2018年数学必修一练习——精选高考题
6.2018年数学必修四练习——精选高考题
高一上期末考部分
1.2017—2018学年高一第一学期期末质量检测(语文)
2.2017—2018学年高一第一学期期末质量检测(数学)必修一二
3.2017—2018学年高一第一学期期末质量检测(数学)必修一三
4.2017—2018学年高一第一学期期末质量检测(数学)必修一四
5..2017—2018学年高一第一学期期末质量检测(英语)
6.2017—2018学年高一第一学期期末质量检测(物理)
7.2017—2018学年高一第一学期期末质量检测(化学)
8.2017—2018学年高一第一学期期末质量检测(生物)
9.2017—2018学年高一第一学期期末质量检测(历史)
10.2017—2018学年高一第一学期期末质量检测(政治)
11.2017—2018学年高一第一学期期末质量检测(地理)
参考答案
一、选择题
1、
【解析】
试题分析:首先画出函数的图象,当时,的零点是,零点左边直线的斜率时,不会和函数有交点,满足不等式恒成立,零点右边,函数的斜率,根据图象分析,当时,,即成立,同理,若 ,函数的零点是,零点右边恒成立,零点左边,根据图象分析当时,,即 ,当时,恒成立,所以,故选A.
【考点】1.分段函数;2.函数图形的应用;3.不等式恒成立.
【名师点睛】一般不等式恒成立求参数1.可以选择参变分离的方法,转化为求函数最值的问题;2.也可以画出两边的函数图象,根据临界值求参数取值范围;3.也可转化为的问题,转化讨论求函数的最值求参数的取值范围.
本题中的函数 和都是比较熟悉的函数,考场中比较快速的方法是就是代入端点,画出函数的图象,快速准确,满足题意时的图象恒不在函数下方,
当时,函数图象如图所示,排除C,D选项;
当时,函数图象如图所示,排除B选项,
2、
【考点】1.指数,对数;2.函数性质的应用
【名师点睛】本题主要考查函数的奇偶性与指数、对数的运算问题,属于基础题型,首先根据奇函数的性质和对数运算法则,,再比较比较大小.
3、
【考点】集合的运算
【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示,若集合是无限集合就用描述法表示,注意代表元素是什么,集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.
4、D
5、B
【解析】
试题分析:,所以函数是奇函数,并且是增函数,
6、C
7、
当时,(*)式为,,
又(当时取等号),
(当时取等号),
所以,
综上.故选A.
【考点】不等式、恒成立问题
【名师点睛】首先满足转化为去解决,由于涉及分段函数问题要遵循分段处理原则,分别对的两种不同情况进行讨论,针对每种情况根据的范围,利用极端原理,求出对应的的范围.
8、
【考点】 指数、对数、函数的单调性
【名师点睛】比较大小是高考常见题,指数式、对数式的比较大小要结合指数函数、对数函数,借助指数函数和对数函数的图象,利用函数的单调性进行比较大小,特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小,还可以解不等式.
9、
【解析】 ,选B.
【考点】 集合的运算
【名师点睛】集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.
10、C
【解析】
试题分析:由时是增函数可知,若,则,所以,由得,解得,则,故选C.
【考点】分段函数求值
【名师点睛】求分段函数的函数值,首先要确定自变量的范围,然后选定相应关系式,代入求解;当给出函数值或函数值的取值范围求自变量的值或自变量的取值范围时,应根据每一段解析式分别求解,但要注意检验所求自变量的值或取值范围是否符合相应段的自变量的值或取值范围.
11、C
【解析】
试题分析:由得,故,故选C.
【考点】 不等式的解法,集合的运算
【名师点睛】对于集合的交、并、补运算问题,应先把集合化简再计算,对连续数集间的运算,借助数轴的直观性,进行合理转化;对已知连续数集间的关系,求其中参数的取值范围时,要注意单独考察等号能否取到,对离散的数集间的运算,或抽象集合间的运算,可借助Venn图.
12、A
【解析】
试题分析:,所以函数是奇函数,并且是增函数, 是减函数,根据增函数-减函数=增函数,所以函数是增函数,故选A.
【考点】函数的性质
【名师点睛】本题属于基础题型,根据奇偶性的定义与的关系就可以判断函数的奇偶性,判断函数单调性的方法,1.平时学习过的基本初等函数的单调性;2.函数图象判断函数的单调性;3.函数的四则运算判断,增函数+增函数=增函数,增函数-减函数=增函数,判断函数的单调性;4.导数判断函数的单调性.
13、B
【解析】根据补集的运算得.故选B.
14、B
【解析】
试题分析:由已知可设,则,因为为偶函数,所以只考虑的情况即可.若,则,所以.故选B.
考点:函数的奇偶性.
15、C
考点:补集的运算.
16、B
【解析】
试题分析:设从2015年后第年该公司全年投入的研发资金开始超过200万元,由已知得,两边取常用对数得
,故选B.
考点:1.增长率问题;2.常用对数的应用.
17、B
考点:集合中交集的运算.
二、填空题
18、
【解析】
试题分析: ,所以当时,取最大值1;当 时,取最小值;因此取值范围为
【考点】二次函数
【名师点睛】本题考查了转化与化归的能力,除了象本题的方法,转化为二次函数求取值范围,也可以转化为几何关系求取值范围,当,表示线段,那么的几何意义就是线段上的点到原点距离的平方,这样会更加简单.
19、
【解析】
【考点】函数奇偶性与周期性
【名师点睛】与函数奇偶性有关问题的解决方法:
①已知函数的奇偶性,求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解.
②已知函数的奇偶性求解析式:将待求区间上的自变量,转化到已知区间上,再利用奇偶性求出,或充分利用奇偶性构造关于f(x)的方程(组),从而得到f(x)的解析式.
③已知函数的奇偶性,求函数解析式中参数的值:常利用待定系数法,利用f(x)±f(-x)=0得到关于待求参数的恒等式,由系数的对等性得参数的值或方程求解.
④应用奇偶性画图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.
20、12
【解析】
21、
考点:反函数的概念以及指对数式的转化.
22、
【解析】试题分析:,故不等式的解集为.
考点:绝对值不等式的基本解法.
23、-2;1.
【解析】
试题分析:,
,
所以,解得.
考点:函数解析式.
24、
【解析】
试题分析:由函数在R上单调递减得,又方程恰有两个不相等的实数解,所以,因此的取值范围是
考点:函数综合
25、-2
【解析】
试题分析:因为函数是定义在上周期为2的奇函数,所以
,所以,即,,所以.
考点:1.函数的奇偶性;2.函数的周期性.
三、简答题
26、试题解析:(Ⅰ)因为
考点:函数的单调性与最值、分段函数.
27、
(2)当时,。
若,则,所以当或时,,函数单调递增;
当时,,函数单调递减;
若时,,,函数单调递增;
(Ⅱ)由(Ⅰ)知时,
,,
令,则,
由可得当且仅当时取等号;
又,设,则在上单调递减,
且,
所以在上存在使得 时,时,,
所以函数在上单调递增;在上单调递减,
由于,因此当且仅当取等号,
所以,即对于任意的恒成立。
考点:利用导函数判断单调性;分类讨论思想.
28、(1).(2)或.(3).
【解析】
试题分析:(1)由,利用得求解.
(2)转化得到,讨论当、时的情况.
(3)讨论在上单调递减.
确定函数在区间上的最大值与最小值之差.得到,对任意
成立.
试题解析: (1)由,得,解得.
(2)有且仅有一解,
等价于有且仅有一解,等价于有且仅有一解.
当时,,符合题意;
当时,,.
综上,或.
(3)当时,,,
所以在上单调递减.
考点:1.对数函数的性质;2.函数与方程;3.二次函数的性质.
29、⑴ ①;②;⑵;
5. ① ,由可得,
则,即,则,;
② 由题意得恒成立,
令,则由可得,
此时恒成立,即恒成立
∵时,当且仅当时等号成立,
因此实数的最大值为.
,,
由,可得,令,则递增,
而,因此时,
因此时,,,则;
时,,,则;
则在递减,递增,因此最小值为,
① 若,时,,,则;
logb2时,,,则;
因此且时,,因此在有零点,
且时,,因此在有零点,
则至少有两个零点,与条件矛盾;
② 若,由函数有且只有1个零点,最小值为,
可得,
由,
因此,
因此,即,即,
因此,则.