- 2021-05-13 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
统计与概率高考题
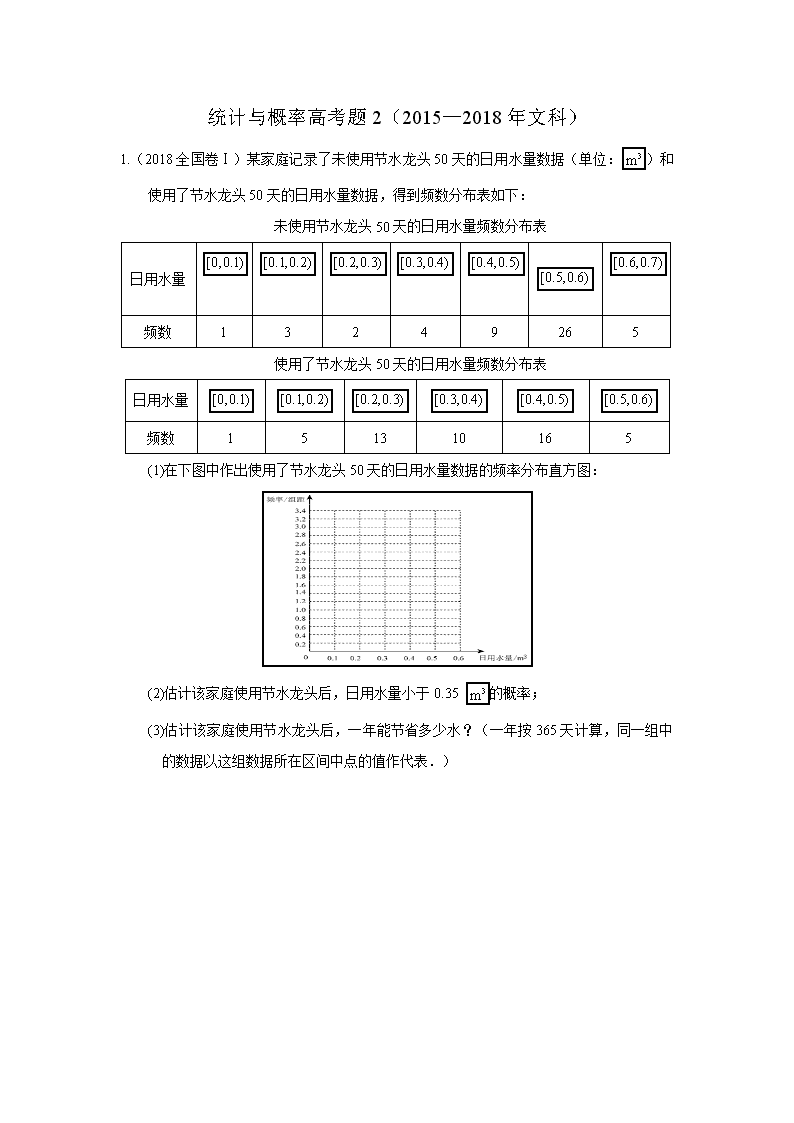
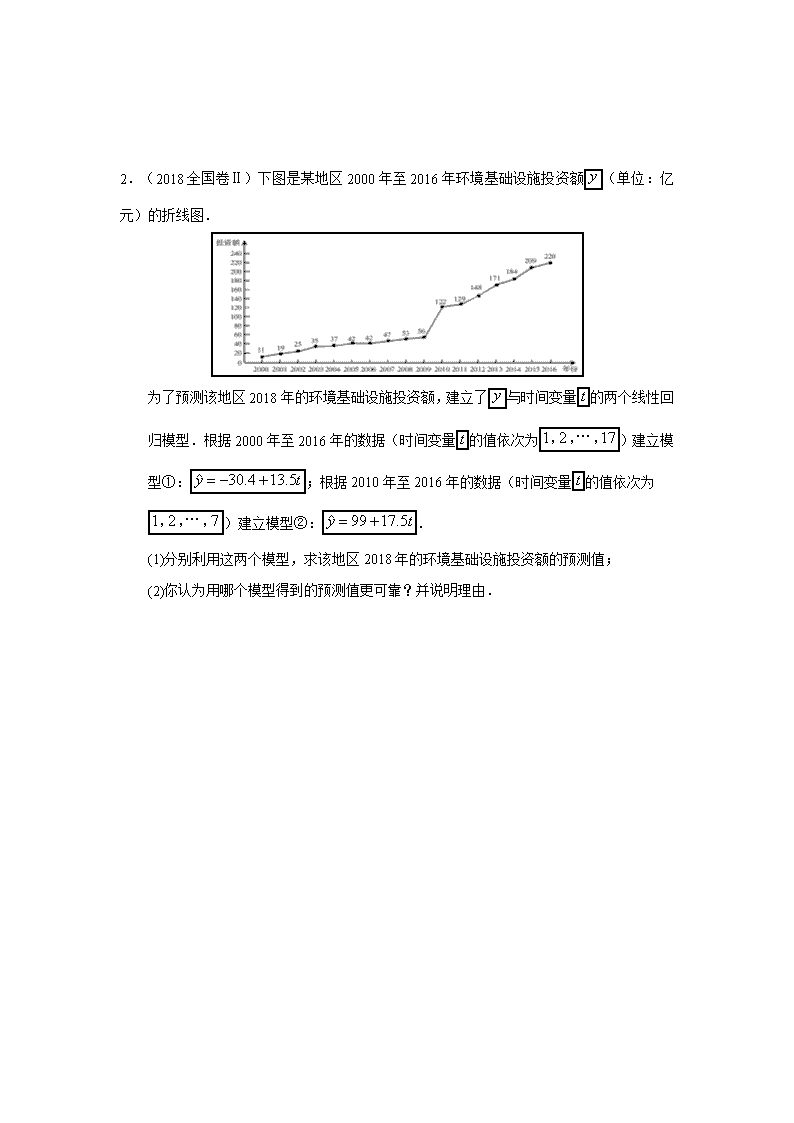
统计与概率高考题 2(2015—2018 年文科) 1.(2018 全国卷Ⅰ)某家庭记录了未使用节水龙头 50 天的日用水量数据(单位: 3m )和使 用了节水龙头 50 天的日用水量数据,得到频数分布表如下: 未使用节水龙头 50 天的日用水量频数分布表 日用水量 [0,0.1) [0.1,0.2) [0.2,0.3) [0.3,0.4) [0.4,0.5) [0.5,0.6) [0.6,0.7) 频数 1 3 2 4 9 26 5 使用了节水龙头 50 天的日用水量频数分布表 日用水量 [0,0.1) [0.1,0.2) [0.2,0.3) [0.3,0.4) [0.4,0.5) [0.5,0.6) 频数 1 5 13 10 16 5 (1)在下图中作出使用了节水龙头 50 天的日用水量数据的频率分布直方图: (2)估计该家庭使用节水龙头后,日用水量小于 0.35 3m 的概率; (3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 365 天计算,同一组中 的数据以这组数据所在区间中点的值作代表.) 2.(2018 全国卷Ⅱ)下图是某地区 2000 年至 2016 年环境基础设施投资额 y (单位:亿元) 的折线图. 为了预测该地区 2018 年的环境基础设施投资额,建立了 y 与时间变量t 的两个线性回 归模型.根据 2000 年至 2016 年的数据(时间变量t 的值依次为1 2 17, ,…, )建立模 型①: ˆ 30.4 13.5 y t ;根据 2010 年至 2016 年的数据(时间变量t 的值依次为 1 2 7, ,…, )建立模型②: ˆ 99 17.5 y t . (1)分别利用这两个模型,求该地区 2018 年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由. 3.(2018 全国卷Ⅲ)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任 务的两种新的生产方式.为比较两种生产方式的效率,选取 40 名工人,将他们随机分 成两组,每组 20 人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根 据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图: (1)根据茎叶图判断哪种生产方式的效率更高?并说明理由; (2)求 40 名工人完成生产任务所需时间的中位数 m ,并将完成生产任务所需时间超过 m 和不超过 m 的工人数填入下面的列联表: 超过 m 不超过 m 第一种生产方式 第二种生产方式 (3)根据(2)中的列联表,能否有 99%的把握认为两种生产方式的效率有差异? 附: 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d , 2( ) 0.050 0.010 0.001 3.841 6.635 10.828 P K k k ≥ 4.(2018 北京)电影公司随机收集了电影的有关数据,经分类整理得到下表: 电影类型 第一类 第二类 第三类 第四类 第五类 第六类 电影部数 140 50 300 200 800 510 好评率 0.4 0.2 0.15 0.25 0.2 0.1 好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. (1)从电影公司收集的电影中随机选取 1 部,求这部电影是获得好评的第四类电影的概 率; (2)随机选取 1 部电影,估计这部电影没有获得好评的概率; (3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生 变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加 0.1,哪类电影的好评率减少 0.1,使得获得好评的电影总部数与样本中的电影总部数 的比值达到最大?(只需写出结论) 5.(2017 新课标Ⅰ)为了监控某种零件的一条生产线的生产过程,检验员每隔 30 min 从该 生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的 16 个零件的尺寸: 抽取次序 1 2 3 4 5 6 7 8 零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 抽取次序 9 10 11 12 13 14 15 16 零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95 经计算得 16 1 1 9.9716 i i x x , 16 16 2 2 2 1 1 1 1( ) ( 16 )16 16i i i i s x x x x 0.212 , 16 2 1 ( 8.5) 18.439 i i , 16 1 ( )( 8.5) 2.78i i x x i ,其中 ix 为抽取的 第i 个零件的尺寸,i =1,2,…,16. (1)求 ( , )ix i ( 1,2, ,16)i 的相关系数 r ,并回答是否可以认为这一天生产的零件 尺寸不随生产过程的进行而系统地变大或变小(若| | 0.25r ,则可以认为零件的尺寸不 随生产过程的进行而系统地变大或变小). (2)一天内抽检零件中,如果出现了尺寸在 ( 3 , 3 )x s x s 之外的零件,就认为这 条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查. (ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查? (ⅱ)在 ( 3 , 3 )x s x s 之外的数据称为离群值,试剔除离群值,估计这条生产线当天生 产的零件尺寸的均值与标准差.(精确到 0.01) 附:样本 ( , )i ix y ( 1,2, , )i n 的相关系数 1 2 2 1 1 ( )( ) ( ) ( ) n i i i n n i i i i x x y y r x x y y , 0.008 0.09 . 6.(2017 新课标Ⅱ)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时 各随机抽取了 100 个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下: (1)记 A 表示事件“旧养殖法的箱产量低于 50kg”,估计 A 的概率; (2)填写下面列联表,并根据列联表判断是否有 99%的把握认为箱产量与养殖方法有关: 箱产量 50kg 箱产量≥50kg 旧养殖法 新养殖法 (3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较。 附: 2( )P K k≥ 0.050 0.010 0.001 k 3.841 6.635 10.828 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d 7.(2017 新课标Ⅲ)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶 4 元, 售价每瓶 6 元,未售出的酸奶降价处理,以每瓶 2 元的价格当天全部处理完.根据往年 销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于 25,需求 量为 500 瓶;如果最高气温位于区间[20,25),需求量为 300 瓶;如果最高气温低于 20, 需求量为 200 瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数 据,得下面的频数分布表: 最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40) 天数 2 16 36 25 7 4 以最高气温位于各区间的频率代替最高气温位于该区间的概率。 (1)求六月份这种酸奶一天的需求量不超过 300 瓶的概率; (2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量 为 450 瓶时,写出Y 的所有可能值,并估计Y 大于零的概率. 8.(2017 北京)某大学艺术专业 400 名学生参加某次测评,根据男女学生人数比例,使用 分层抽样的方法从中随机抽取了 100 名学生,记录他们的分数,将数据分成 7 组: [20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图: (Ⅰ)从总体的 400 名学生中随机抽取一人,估计其分数小于 70 的概率; (Ⅱ)已知样本中分数小于 40 的学生有 5 人,试估计总体中分数在区间[40,50)内的 人数; (Ⅲ)已知样本中有一半男生的分数不小于 70,且样本中分数不小于 70 的男女生人数 相等.试估计总体中男生和女生人数的比例. 9.(2016 年全国 I 卷)某公司计划购买 1 台机器,该种机器使用三年后即被淘汰.机器有一 易损零件,在购进机器时,可以额外购买这种零件作为备件,每个 200 元.在机器使用 期间,如果备件不足再购买,则每个 500 元.现需决策在购买机器时应同时购买几个易 损零件,为此搜集并整理了 100 台这种机器在三年使用期内更换的易损零件数,得下面 柱状图: 记 x 表示 1 台机器在三年使用期内需更换的易损零件数,y 表示 1 台机器在购买易损零 件上所需的费用(单位:元), n 表示购机的同时购买的易损零件数. (I)若 n =19,求 y 与 x 的函数解析式; (II)若要求“需更换的易损零件数不大于 n ”的频率不小于 0.5,求 n 的最小值; (III)假设这 100 台机器在购机的同时每台都购买 19 个易损零件,或每台都购买 20 个 易损零件,分别计算这 100 台机器在购买易损零件上所需费用的平均数,以此作为 决策依据,购买 1 台机器的同时应购买 19 个还是 20 个易损零件? 10.(2016 年全国 II 卷)某险种的基本保费为 a (单位:元),继续购买该险种的投保人称 为续保人,续保人本年度的保费与其上年度出险次数的关联如下: 上年度出险次数 0 1 2 3 4 5≥ 保费 0.85a a 1.25a 1.5a 1.75a 2a 随机调查了该险种的 200 名续保人在一年内的出险情况,得到如下统计表: 出险次数 0 1 2 3 4 5≥ 频数 60 50 30 30 20 10 (Ⅰ)记 A 为事件:“一续保人本年度的保费不高于基本保费”。求 ( )P A 的估计值; (Ⅱ)记 B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的 160%”.求 ( )P B 的估计值; (III)求续保人本年度的平均保费估计值. 11.(2016 年全国 III 卷)如图是我国 2008 年至 2014 年生活垃圾无害化处理量(单位:亿 吨)的折线图. 注:年份代码 1–7 分别对应年份 2008–2014. (Ⅰ)由折线图看出,可用线性回归模型拟合 y 与t 的关系,请用相关系数加以说明; (Ⅱ)建立 y 关于t 的回归方程(系数精确到 0.01),预测 2016 年我国生活垃圾无害化 处理量. 附注:参考数据: 7 1 9.32i i y , 7 1 40.17i i i t y , 7 2 1 ( ) 0.55i i y y , 7 ≈2.646. 参考公式:相关系数 1 2 2 1 1 ( )( ) ( ) (y y) n i i i n n i i i i t t y y r t t , 回归方程 y a bt 中斜率和截距的最小二乘估计公式分别为: 1 2 1 ( )( ) ( ) n i i i n i i t t y y b t t , = .a y bt 12.(2016 年北京)某市民用水拟实行阶梯水价.每人用水量中不超过 w 立方米的部分按 4 元/立方米收费,超出 w 立方米的部分按 10 元/立方米收费.从该市随机调查了 10000 位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图: (Ⅰ)如果 w 为整数,那么根据此次调查,为使 80%以上居民在该月的用水价格为 4 元/立方米, w 至少定为多少? (Ⅱ)假设同组中的每个数据用该组区间的右端点值代替.当 w =3 时,估计该市居民 该月的人均水费. 13.(2015 新课标 1)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 x (单 位:千元)对年销售量 y (单位:t )和年利润 z (单位:千元)的影响,对近 8 年的 年宣传费 ix 和年销售量 iy (i =1,2,···,8)数据作了初步处理,得到下面的散点图及 一些统计量的值. x y w 8 2 1 ( )i i x x 8 2 1 ( )i i w w 8 1 ( )( )i i i x x y y 8 1 ( )( )i i i w w y y 46.6 563 6.8 289.8 1.6 1469 108.8 表中 i iw x , w = 1 8 8 1 i i w . (Ⅰ)根据散点图判断,y a bx 与 y c d x 哪一个适宜作为年销售量 y 关于年 宣传费 x 的回归方程类型?(给出判断即可,不必说明理由) (Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立 y 关于 x 的回归方程; (Ⅲ)已知这种产品的年利率 z 与 x 、 y 的关系为 0.2z y x .根据(Ⅱ)的结果回 答下列问题: (ⅰ)年宣传费 49x 时,年销售量及年利润的预报值是多少? (ⅱ)年宣传费 x 为何值时,年利率的预报值最大? 附:对于一组数据 1 1( , )u v , 2 2( , )u v , ,( , )n nu v ,其回归线 v u 的斜率和截 距的最小二乘估计分别为 1 2 1 ( )( ) ˆ ( ) n i i i n i i u u v v u u , ˆˆ v u . 14.(2015 新课标Ⅱ)某公司为了解用户对其产品的满意度,从 ,A B 两地区分别随机调查了 40 个用户,根据用户对产品的满意度评分,得分 A 地区用户满意评分的频率分布直方 图和 B 地区用户满意度评分的频数分布表. B 地区用户满意度评分的频数分布表 满意度评 分分组 [50,60) [60,70) [70,80) [80,90) [90,100) 频数 2 8 14 10 6 (Ⅰ)在答题卡上作出 B 地区用户满意度评分的频数分布直方图,并通过直方图比较 两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可); (Ⅱ)根据用户满意度评分,将用户的满意度分为三个等级; 满意度评分 低于 70 分 70 分到 80 分 不低于 90 分 满意度等级 不满意 满意 非常满意 估计哪个地区用户的满意度等级为不满意的概率大?说明理由. 15.(2015 北京)某超市随机选取 1000 位顾客,记录了他们购买甲、乙、丙、丁四种商品 的情况,整理成下统计表,其中“√”表示购买,“×”表示未购买. 商品 顾客人数 甲 乙 丙 丁 100 √ × √ √ 217 × √ × √ 200 √ √ √ × 300 √ × √ × 85 √ × × × 98 × √ × × (Ⅰ)估计顾客同时购买乙和丙的概率; (Ⅱ)估计顾客在甲、乙、丙、丁中同时购买 3 种商品的概率; (Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大?查看更多