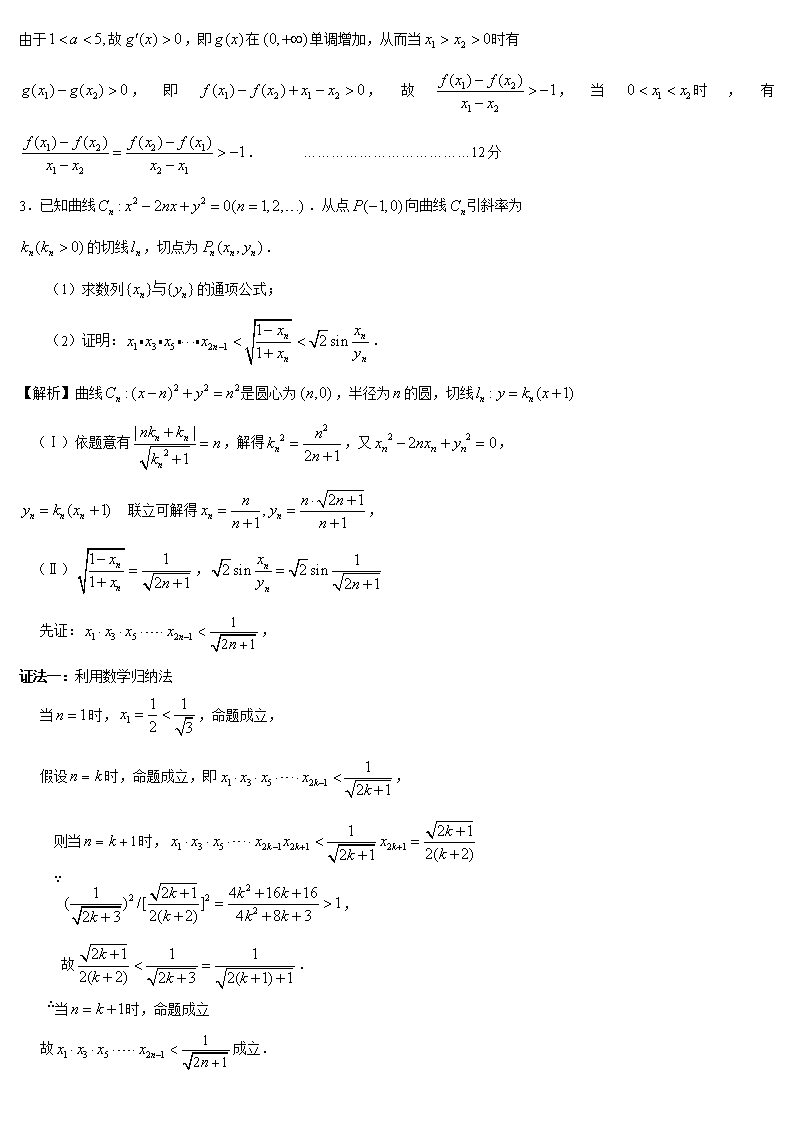新构造函数法在高考解导数和数列问题中的广泛应用
构造函数法在高考解导数和数列问题中的广泛应用
函数与方程数学思想方法是新课标要求的一种重要的数学思想方法,构造函数法便是其中的一种,下面就源于两个重要极限
的不等式利用近三年高考题举例加以说明。
1.设函数 在 R 上的导函数为 ,且 ,下面的不等式在 R 上恒成立的是
A. B. C. D.
【答案】A
【解析】由已知,首先令 得 ,排除 B,D.
令 ,则 ,
① 当 时 , 有 , 所 以 函 数 单 调 递 增 , 所 以 当 时 ,
,从而 .
② 当 时 , 有 , 所 以 函 数 单 调 递 减 , 所 以 当 时 ,
,从而 .综上 .故选 A.
【考点定位】本试题考察了导数来解决函数单调性的运用.通过分析解析式的特点,考查了分析问题和解决问题的能力.
2.已知函数 , .
(Ⅰ)讨论函数 的单调性;
(Ⅱ)证明:若 ,则对任意 , ,有 .
解:(Ⅰ) 的定义域为 .
…………………2 分
(i)若 即 ,则 ,
故 在 单调增加.
(ii)若 ,而 ,故 ,则当 时, ;
当 及 时, .故 在 单调减少,
在 单调增加.
(iii)若 ,即 ,同理可得 在 单调减少,在 单调增加.
(II)考虑函数 .
则 .
( )f x ( )f x′ 22 ( ) ( )f x xf x x′+ >
0)( >xf 0)(
)( xxf <)(
0=x 0)( >xf
2( ) ( )g x x f x= [ ]( ) 2 ( ) ( )g x x f x xf x′ ′= +
0x > 2( )2 ( ) ( ) ( ) 0g xf x xf x x g xx
′′ ′+ = > ⇒ > ( )g x 0x >
( ) (0) 0g x g> = 0)( >xf
0x < 2( )2 ( ) ( ) ( ) 0g xf x xf x x g xx
′′ ′+ = > ⇒ < ( )g x 0x <
( ) (0) 0g x g> = 0)( >xf 0)( >xf
21( ) ( 1)ln2f x x ax a x= − + − 1a >
( )f x
5a < 1 2, (0, )x x ∈ +∞ 1 2x x≠ 1 2
1 2
( ) ( ) 1f x f x
x x
− > −−
( )f x (0, )+∞
21 1 ( 1)( 1 )( ) a x ax a x x af x x a x x x
− − + − − + −′ = − + = =
1 1a − = 2a =
2( 1)( ) xf x x
−′ =
( )f x (0, )+∞
1 1a − < 1a > 1 2a< < ( 1,1)x a∈ − ' ( ) 0f x <
(0, 1)x a∈ − (1, )x∈ +∞ ' ( ) 0f x > ( )f x ( 1,1)a −
(0, 1),(1, )a − +∞
1 1a − > 2a > ( )f x (1, 1)a − (0,1),( 1, )a − +∞
( ) ( )g x f x x= + 21 ( 1)ln2 x ax a x x= − + − +
21 1( ) ( 1) 2 ( 1) 1 ( 1 1)a ag x x a x a ax x
− −′ = − − + ≥ ⋅ − − = − − −
由于 故 ,即 在 单调增加,从而当 时有
, 即 , 故 , 当 时 , 有
. ………………………………12 分
3.已知曲线 .从点 向曲线 引斜率为
的切线 ,切点为 .
(1)求数列 的通项公式;
(2)证明: .
【解析】曲线 是圆心为 ,半径为 的圆,切线
(Ⅰ)依题意有 ,解得 ,又 ,
联立可解得 ,
(Ⅱ) ,
先证: ,
证法一:利用数学归纳法
当 时, ,命题成立,
假设 时,命题成立,即 ,
则当 时,
∵ ,
故 .
∴当 时,命题成立
故 成立.
1 5,a< < ( ) 0g x′ > ( )g x (0, )+∞ 1 2 0x x> >
1 2( ) ( ) 0g x g x− > 1 2 1 2( ) ( ) 0f x f x x x− + − > 1 2
1 2
( ) ( ) 1f x f x
x x
− > −− 1 20 x x< <
1 2 2 1
1 2 2 1
( ) ( ) ( ) ( ) 1f x f x f x f x
x x x x
− −= > −− −
2 2: 2 0( 1,2, )nC x nx y n− + = = ( 1,0)P − nC
( 0)n nk k > nl ( , )n n nP x y
{ } { }n nx y与
1 3 5 2 1
1 2 sin1
n n
n
n n
x xx x x x x y−
−⋅⋅⋅ < <+
2 2 2:( )nC x n y n− + = ( ,0)n n : ( 1)n nl y k x= +
2
| |
1
n n
n
nk k n
k
+ =
+
2
2
2 1n
nk n
= +
2 22 0n n nx nx y− + =
( 1)n n ny k x= + 2 1,1 1n n
n n nx yn n
⋅ += =+ +
1 1
1 2 1
n
n
x
x n
− =+ +
12 sin 2 sin
2 1
n
n
x
y n
=
+
1 3 5 2 1
1
2 1nx x x x
n−⋅ ⋅ ⋅ ⋅ <
+
1n = 1
1 1
2 3
x = <
n k= 1 3 5 2 1
1
2 1kx x x x
k−⋅ ⋅ ⋅ ⋅ <
+
1n k= + 1 3 5 2 1 2 1 2 1
1 2 1
2( 2)2 1k k k
kx x x x x x kk− + +
+⋅ ⋅ ⋅ ⋅ < = ++
2
2 2
2
1 2 1 4 16 16( ) /[ ] 12( 2) 4 8 32 3
k k k
k k kk
+ + += >+ + ++
2 1 1 1
2( 2) 2 3 2( 1) 1
k
k k k
+ < =+ + + +
1n k= +
1 3 5 2 1
1
2 1nx x x x
n−⋅ ⋅ ⋅ ⋅ <
+
证法二: , ,
下证: .
不妨设 ,令 ,
则 在 上恒成立,故 在 上单调递减,
从而 ,即 .
综上, 成立.
4.【09 全国Ⅱ·理】22.(本小题满分 12 分)
设函数 有两个极值点 ,且 .
(I)求 的取值范围,并讨论 的单调性;
(II)证明: .
【解】(I)由题设知,函数 的定义域是
且 有两个不同的根 ,故 的判别式 ,即
且 …………………………………①
又 故 .因此 的取值范围是 .
当 变化时, 与 的变化情况如下表:
11 11
1 2 11 1
n
n
n
x n
nx n
n
−− += =+ ++ +
12
12
14
)12(
4
)12(
2
12
2
2
2
2
+
−=−
−<−=−
n
n
n
n
n
n
n
n
n
n
n x
x
nn
n
n
nxxxx +
−=+=+
−×××<−×××=⋅⋅⋅⋅ − 1
1
12
1
12
12
5
3
3
1
2
12
4
3
2
1
12531
1 12 sin
2 1 2 1n n
<
+ +
1 3(0, ]32 1
t
n
= ∈
+ ( ) 2 sinf t t t= −
( ) 1 2cos 0f t t′ = − < 3(0, ]3t ∈ ( ) 2 sinf t t t= − 3(0, ]3t ∈
( ) 2 sin (0) 0f t t t f= − < = 1 12 sin
2 1 2 1n n
<
+ +
1 3 5 2 1
1 2 sin1
n n
n
n n
x xx x x x x y−
−⋅ ⋅ ⋅ ⋅ < <+
( ) ( )2 1f x x aln x= + + 1 2x x, 1 2x x<
a ( )f x
( )2
1 2 2
4
lnf x
−>
( )f x 1,x > −
( ) 22 2 ,1
x x af x x
+ +′ = +
( ) 0f x′ = 1 2x x、 22 2 0x x a+ + = 4 8 0a∆ = − > 1 ,2a <
1 2
1 1 2 1 1 2, .2 2
a ax x
− − − − + −= =
1 1,x > − 0a > a 1(0, )2
x ( )f x ( )f x′
因此 在区间 和 是增函数,在区间 是减函数.
(II)由题设和①知
于是 .
设函数
则
当 时, ;
当 时, 故 在区间 是增函数.
于是,当 时,
因此 .
5.【2008 年山东理】 21.(本题满分 12 分)
已知函数 其中 为常数.
(I)当 时,求函数 的极值;
(II)当 时,证明:对任意的正整数 ,当 时,有
【标准答案】
(Ⅰ)解:由已知得函数 的定义域为 ,
当 时, ,所以 .
(1)当 时,由 得 , ,
此时 .
当 时, , 单调递减;
当 时, , 单调递增.
(2)当 时, 恒成立,所以 无极值.
综上所述, 时,
当 时, 在 处取得极小值,极小值为 .
当 时, 无极值.
( )f x 1( 1, )x− 2( , )x +∞ 1 2( , )x x
2 2 2
1 0, 2 (1 ),2 x a x x− < < = − +
( ) ( )2
2 2 2 2 22 (1 ) 1f x x x x ln x= − + +
( ) ( )2 2 (1 ) 1 ,g t t t t ln t= − + +
( ) ( )2 (1 2 ) 1g t t t ln t′ = − + +
1
2t = − ( ) 0g t′ =
1( ,0)2t ∈ − ( ) 0,g t′ > ( )g t 1[ ,0)2
−
1( ,0)2t ∈ − ( ) 1 1 2 2( ) .2 4
lng t g
−> − =
( )2 2
1 2 2( ) 4
lnf x g x
−= >
1( ) ln( 1),1 )nf x a xx
= + −−(
*,n N∈ a
2n = ( )f x
1a = n 2x ≥ ( ) 1.f x x≤ −
( )f x { }| 1x x >
2n = 2
1( ) ln( 1)(1 )f x a xx
= + −−
2
3
2 (1 )( ) (1 )
a xf x x
− −′ = −
0a > ( ) 0f x′ = 1
21 1x a
= + > 2
21 1x a
= − <
1 2
3
( )( )( ) (1 )
a x x x xf x x
− − −′ = −
1(1 )x x∈ , ( ) 0f x′ < ( )f x
1( )x x∈ + ∞, ( ) 0f x′ > ( )f x
0a ≤ ( ) 0f x′ < ( )f x
2n =
0a > ( )f x 21x a
= + 2 21 1 ln2
af a a
+ = +
0a ≤ ( )f x
(Ⅱ)证法一:因为 ,所以 .
当 为偶数时,
令 ,
则 ( ).
所以 当 时, 单调递增,
又 ,
因此 恒成立,
所以 成立.
当 为奇数时,
要证 ,由于 ,所以只需证 ,
令 ,
则 ( ),
所以 当 时, 单调递增,又 ,
所以当 时,恒有 ,即 命题成立.
综上所述,结论成立.
证法二:当 时, .
当 时,对任意的正整数 ,恒有 ,
故只需证明 .
令 , ,
则 ,
当 时, ,故 在 上单调递增,
因此 当 时, ,即 成立.
故 当 时,有 .
1a = 1( ) ln( 1)(1 )nf x xx
= + −−
n
1( ) 1 ln( 1)(1 )ng x x xx
= − − − −−
1 1
1 2( ) 1 0( 1) 1 1 ( 1)n n
n x ng x x x x x+ +
−′ = + − = + >− − − − 2x ≥
[ )2x∈ + ∞, ( )g x
(2) 0g =
1( ) 1 ln( 1) (2) 0( 1)ng x x x gx
= − − − − =−
≥
( ) 1f x x −≤
n
( ) 1f x x −≤ 1 0(1 )nx
<− ln( 1) 1x x− −≤
( ) 1 ln( 1)h x x x= − − −
1 2( ) 1 01 1
xh x x x
−′ = − =− −
≥ 2x ≥
[ )2x∈ + ∞, ( ) 1 ln( 1)h x x x= − − − (2) 1 0h = >
2x ≥ ( ) 0h x > ln( 1) 1x x− < −
1a = 1( ) ln( 1)(1 )nf x xx
= + −−
2x ≥ n 1 1(1 )nx−
≤
1 ln( 1) 1x x+ − −≤
( ) 1 (1 ln( 1)) 2 ln( 1)h x x x x x= − − + − = − − − [ )2x∈ + ∞,
1 2( ) 1 1 1
xh x x x
−′ = − =− −
2x ≥ ( ) 0h x′ ≥ ( )h x [ )2 + ∞,
2x ≥ ( ) (2) 0h x h =≥ 1 ln( 1) 1x x+ − −≤
2x ≥ 1 ln( 1) 1(1 )n x xx
+ − −−
≤
即 .
【试题分析】第一问对 讨论时要注意一些显而易见的结果,当 时 恒成立, 无极值.第二问需要对构
造的新函数 进行“常规处理”,即先证单调性,然后求最值 ,最后作出判断.
【高考考点】导数及其应用、构造函数证明不等式
【易错提醒】没有注意该函数定义域对问题的影响,分类讨论无目标,判断
的正负漏掉符号.
【学科网备考提示】函数类问题的解题方法要内悟、归纳、整理,使之成为一个系统,在具体运用时自如流畅,既要具有一
定的思维定向,也要谨防盲目套用.此类问题对转化能力要求很高,不能有效转化是解题难以突破的主要原因,要善于构造
函数证明不等式,从而体现导数的工具性.
6.【2007 年山东理】 (22)(本小题满分 14 分)
设函数 ,其中 .
(I)当 时,判断函数 在定义域上的单调性;
(II)求函数 的极值点;
(III)证明对任意的正整数 ,不等式 都成立.
【解】(Ⅰ)由题意知, 的定义域为 ,
设 ,其图象的对称轴为 ,
当 时, ,即 在 上恒成立,
当 时, ,
当 时,函数 在定义域 上单调递增
(Ⅱ)①由(Ⅰ)得:当 时,函数 无极值点
② 时, 有两个相同的解 ,
时, , 时, ,
时,函数 在 上无极值点
③当 时, 有两个不同解, , ,
( ) 1f x x −≤
a 0a ≤ / ( ) 0f x < ( )f x
( )h x
/ 1 2
3
( )( )( ) 1 )
a x x x xf x x
− − −= −(
2( ) ln( 1)f x x b x= + + 0b ≠
1
2b > ( )f x
( )f x
n 2 3
1 1 1ln( 1)n n n
+ > −
( )f x ( 1 )− + ∞,
22 2( ) 2 1 1
b x x bf x x x x
+ +′ = + =+ +
2( ) 2 2g x x x b= + + 1 ( 1 )2x = − ∈ − + ∞,
max
1 1( ) 2 2g x g b ∴ = − = − +
1
2b > max
1( ) 02g x b= − + > 2( ) 2 2 0g x x x b= + + > ( 1 )− + ∞,
∴ ( 1 )x∈ − + ∞, ( ) 0f x′ >
∴ 1
2b > ( )f x ( 1 )− + ∞,
1
2b > ( )f x
1
2b =
212 2( ) 01
x
f x x
+ ′ = =+
1
2x = −
11 2x ∈ − − , ( ) 0f x′ > 1
2x ∈ − + ∞ , ( ) 0f x′ >
1
2b∴ = ( )f x ( 1 )− + ∞,
1
2b < ( ) 0f x′ = 1
1 1 2
2
bx
− − −= 2
1 1 2
2
bx
− + −=
时, , ,
即 ,
时, , 随 的变化情况如下表:
极小值
由此表可知: 时, 有惟一极小值点 ,
当 时, , ,
此时, , 随 的变化情况如下表:
极大值 极小值
由此表可知: 时, 有一个极大值 和一个极小值点
;
综上所述: 时, 有惟一最小值点 ;
时, 有一个极大值点 和一个极小值点 ;
时, 无极值点
(Ⅲ)当 时,函数 ,
令函数 ,
则 .
当 时, ,所以函数 在 上单调递增,
又 时,恒有 ,即 恒成立
0b < 1
1 1 2 12
bx
− − −= < − 2
1 1 2 02
bx
− + −= >
1 ( 1 )x ∉ − + ∞, [ )2 1x ∈ − + ∞,
0b∴ < ( )f x′ ( )f x x
x 2( 1 )x− , 2x 2( )x + ∞,
( )f x′ − 0 +
( )f x
0b < ( )f x 2
1 1 2
2
bx
− + −=
10 2b< < 1
1 1 2 12
bx
− − −= > − 1 2 ( 1 )x x∴ ∈ − + ∞,
( )f x′ ( )f x x
x 1( 1 )x− , 1x 1 2( )x x, 2x 2( )x + ∞,
( )f x′ + 0 − 0 +
( )f x
10 2b< < ( )f x 1
1 1 2
2
bx
− − −=
2
1 1 2
2
bx
− + −=
0b < ( )f x 2
1 1 2
2
bx
− + −=
10 2b< < ( )f x 1 1 2
2
bx
− − −= 1 1 2bx x
− + −=
1
2b ≥ ( )f x
1b = − 2( ) ln( 1)f x x x= − +
3 3 2( ) ( ) ln( 1)h x x f x x x x= − = − + +
3 2
2 1 3 ( 1)( ) 3 2 1 1
x xh x x x x x
+ −′ = − + =+ +
∴ [ )0x∈ + ∞, ( ) 0h x′ > ( )h x [ )0 + ∞,
(0) 0h = (0 )x∴ ∈ + ∞, ( ) (0) 0h x h> = 3 2 ln( 1)x x x> − +
故当 时,有 .
对任意正整数 取 ,则有
所以结论成立.
7.【2008 年湖南理】 21.(本小题满分 13 分)
已知函数 .
(I)求函数 的单调区间;
(Ⅱ)若不等式 对任意的 都成立(其中 是自然对数的底数).
求 的最大值.
解: (Ⅰ)函数 的定义域是 ,
设 ,则
令 则
当 时, 在 上为增函数,
当 x>0 时, 在 上为减函数.
所以 在 处取得极大值,而 ,所以 ,
函数 在 上为减函数.
于是当 时,
当 时,
所以,当 时, 在 上为增函数.
当 时, 在 上为减函数.
故函数 的单调递增区间为 ,单调递减区间为 .
(Ⅱ)不等式 等价于不等式 由 知,
设 则
(0 )x∈ + ∞, 2 3ln( 1)x x x+ > −
n 1 (0 )x n
= ∈ + ∞, 2 3
1 1 1ln 1n n n
+ > −
2
2( ) ln (1 ) 1
xf x x x
= + − +
( )f x
1(1 )n a en
++ ≤ N*n∈ e
a
( )f x ( 1, )− +∞
2 2
2 2
2ln(1 ) 2 2(1 )ln(1 ) 2( ) .1 (1 ) (1 )
x x x x x x xf x x x x
+ + + + − −′ = − =+ + +
2( ) 2(1 )ln(1 ) 2g x x x x x= + + − − ( ) 2ln(1 ) 2 .g x x x′ = + −
( ) 2ln(1 ) 2 ,h x x x= + − 2 2( ) 2 .1 1
xh x x x
−′ = − =+ +
1 0x− < < ( ) 0,h x′ > ( )h x ( 1,0)−
( ) 0,h x′ < ( )h x (0, )+∞
( )h x 0x = ( ) 0h x = ( ) 0( 0)g x x′ < ≠
( )g x ( 1, )− +∞
1 0x− < < ( ) (0) 0,g x g> =
0x > ( ) (0) 0.g x g< =
1 0x− < < ( ) 0,f x′ > ( )f x ( 1,0)−
0x > ( ) 0,f x′ < ( )f x (0, )+∞
( )f x ( 1,0)− (0, )+∞
1(1 )n a en
++ ≤ 1( )ln(1 ) 1.n a n
+ + ≤ 11 1n
+ >
1 .1ln(1 )
a n
n
≤ −
+
( ]1 1( ) , 0,1 ,ln(1 )G x xx x
= − ∈+
由(Ⅰ)知, 即
所以 于是 在 上为减函数.
故函数 在 上的最小值为
所以 a 的最大值为
1.2009 潍坊文科(22)(本小题满分 14 分)
设函数 表示 的导函数.
(I)求函数 的单调递增区间;
(Ⅱ)当 k 为偶数时,数列{ }满足 ,求数列{ }的通项公式;
(Ⅲ)当 k 为奇数时, 设 ,数列 的前 项和为 ,证明不等式
对一切正整数 均成立,并比较 与 的大小.
解:(Ⅰ)函数的定义域为(0,+∞),
又 , …………1 分
当 k 为奇数时, ,
即 的单调递增区间为 . …………2 分
当 k 为偶函数时,
由 ,得 ,即 的单调递增区间为 ,
综上所述:当 k 为奇数时, 的单调递增区间为 ,
当 k 为偶数时, 的单调递增区间为 …………4 分
(Ⅱ)当 k 为偶数时,由(Ⅰ)知
2 2
2 2 2 2
1 1 (1 )ln (1 )( ) .(1 )ln (1 ) (1 )ln (1 )
x x xG x x x x x x x
+ + −′ = − + =+ + + +
2
2ln (1 ) 0,1
xx x
+ − ≤+
2 2(1 )ln (1 ) 0.x x x+ + − ≤
( ) 0,G x′ < ( ]0,1 ,x∈ ( )G x ( ]0,1
( )G x ( ]0,1 1(1) 1.ln 2G = −
1 1.ln 2
−
2( ) 2( 1) ln ( ), ( )kf x x x k N f x∗ ′= − − ∈ ( )f x
( )y f x=
na 2
1 11, ( ) 3n n na a f a a +′= = − 2
na
( )1
2nb f n n′= − { }nb n nS
( ) 1
1
1 nbnb e++ > n 2009 1S − 2009ln
21 2[ ( 1) ]( ) 2 2( 1)
k
k xy f x x x x
− −′ ′= = − − =
01
22( 1)( ) xf x x
+′ =
(0, ), ( ) 0 (0, )x f x′∈ +∞ ∴ > +∞ 在 恒成立.
( )f x′ (0, )+∞
02
22( 1) 2( 1)( 1)( ) x x xf x x x
− + −′ = =
(0, ), 0, 1 0,x x x∈ +∞ > + >又
( ) 0f x′ > 1 0, 1x x− > ∴ > ( )f x (1, )+∞
( )f x (0, )+∞
( )f x (1, ).+∞
22( 1)( ) xf x x
−′ =
所以
根据题设条件有
∴{ }是以 2 为公比的等比数列,
∴ ………………………………8 分
(Ⅲ)由(Ⅰ)知,当 k 为奇数时,
由已知要证 两边取对数,即证 …………………10 分
事实上:设 则
因此得不等式 …………………………………………①
构造函数 下面证明 在 上恒大于 0.
∴ 在 上单调递增,
即
∴ ∴
即 成立. ………………………………………………………12 分
由
得
即
当 时, ……………………………………………14 分
2.山东省日照市 2009 届高三模拟考试数学理科试题(22)(本小题满分 14 分)
已知 ,函数 .
(Ⅰ)试问在定义域上能否是单调函数?请说明理由;
(Ⅱ)若 在区间 上是单调递增函数,试求实数 的取值范围;
(Ⅲ)当 时,设数列 的前 项和为 ,求证:
( )f x [ )1,+∞ a
1a = 1
n
n
22( 1)( ) .n
n
n
af a a
−′ =
2 2 2 2 2 2
1 1 12( 1) 3, 2 1, 1 2( 1),n n n n n na a a a a a+ + +− = − ∴ = + + = +
2 1na +
2 2 1 2
11 ( 1) 2 2 , 2 1.n n n
n na a a−+ = + ⋅ = ∴ = −
12( ),f x x
′ = +
1 1 1 1 1( ) , 1 .2 2 3n nb f n n Sn n
′∴ = − = = + + +⋅⋅⋅+
111 ,
n
en
+ + >
1 1ln 1 ,1n n
+ > +
11 ,tn
+ = 1 ( 1),1n tt
= >−
1ln 1 ( 1)t tt
> − >
1( ) ln 1( 1),g t t tt
= + − > ( )g t (1, )+∞
2
1 1( ) 0,g t t t
′ = − >
( )g t (1, )+∞ ( ) (1) 0,g t g> =
1ln 1 ,t t
> −
1 1ln 1 ,1n n
+ > +
111 ,
n
en
+ + >
( ) 1
1
1 nbnb e++ >
1 1ln ,1
n
n n
+ > +
1 1 1 2 3 1ln ln ln ln( 1),2 3 1 1 2
n nn n
++ +⋅⋅⋅+ < + +⋅⋅⋅+ = ++
1 1 ln( 1),nS n+ − < +
2008n = 2009 1S − < 2009.ln
0a > 1( ) lnxf x xax
−= +
nS
解:
(Ⅰ) 的定义域为 , ,由 得 . ……2 分
当 时, , 递减;
当 时, , 递增.
所以 不是定义域上的单调函数. ……………………………4 分
(Ⅱ)若 在 是单调递增函数,则 恒成立,即 恒成立.
………………………….…6 分
即 . ……………8 分
(Ⅲ)当 时,由(Ⅱ)知, 在 上为增函数,
又 当 时, , ,即 .
令 则 ,当 时,
从而函数 在 上是递增函数,所以有 即得
综上有: ………………………………10 分
………………………………………12 分
令 时,不等式 也成立,
于是代入,将所得各不等式相加,得
即
即 ……………………14 分
3.山东省枣庄市 2009 届高三年级调研考试数学理 21.(本小题满分 12 分)
已知函数 ,如果
在其定义域上是增函数,且 存在零点( 的导函数).
(I)求 的值;
( II ) 设 是 函 数 的 图 象 上 两 点 ,
1
11 ( ) ( 2)n n
nS f n S n N nn −
−− < − < ∈ ∗ ≥且
( )f x ( )0,+∞ 2
1( ) axf x ax
−′ = ( ) 0f x′ = 1x a
=
1( , )x a a
∈ ( ) 0f x′ < ( )f x
1( , )x a
∈ +∞ ( ) 0f x′ > ( )f x
( )y f x=
( )f x x∈ [1, )+∞ ( ) 0f x′ ≥ 1a x
≥
1 max, [1, )a xx
≥ ∈ +∞
1 1x
∴ ≤ 1a∴ ≥
1a = 1( ) lnxf x xx
−= + [1, )+∞
1 1 1( ) ln ln ,n n nf n n nn n n
− − −− = + − =
1x > ( ) (1)f x f> 1 ln 0x xx
−∴ + > 1ln 1x x
> −
( ) 1 ln ,g x x x= − − 1( ) 1g x x
′ = − (1, )x∈ +∞ ( ) 0.g x′ >
( )g x [1, )+∞ ( ) (1) 0,g x g> = 1 ln .x x− >
11 ln 1,( 1).x x xx
− < < − >
1 1 1ln .1
x
x x x
+∴ < <+
1,2,..., 1,( 2)x n n N n∗= − ∈ ≥且 1 1 1ln .1
x
x x x
+∴ < <+
1 1 1 2 3 1 1... ln ln ... ln 1 ... .2 3 1 2 1 2 1
n
n n n
+ + + < + + + < + + +− −
1 1 1 1 1... ln 1 ... .2 3 2 1nn n
+ + + < < + + + −
1
11 ( ) ( 2).n n
nS f n S n N nn
∗
−
−− < − < ∈ ≥且
为常数其中且 aaaxxgxxxf a ),1,0(log)(,22
1)( 2 ≠>=−=
)()()( xgxfxh += ( )h x′ ( ) ( )h x h x′ 为
a
( , ( )), ( , ( ))( )A m g m B n g n m n< ( )y g x= 0
( ) ( )( ) g n g mg x n m
−′ = −
0( ( ) ( ) ), : .g x g x m x n′ < <为 的导函数 证明
解:(I)因为
所以
因为 上是增函数.
所以 上恒成立 ……………………………1 分
当
而 上的最小值是 1.
于是 (※)
可见
从而由(※)式即得 ① ………………..………………………… 4 分
同时,
由
解得 ②,或
由①②得
此时, 即为所求 ……………………………6 分
注:没有提到(验证) 时, 不扣分.
(II)由(I),
于是 ……………………………7 分
以下证明 (☆)
(☆)等价于 ……………………………8 分
构造函数
则 时,
上为增函数.
因此当 即
从而 得到证明. ……………………………11 分
同理可证 ……………………………12 分
注:没有“综上”等字眼的结论,扣 1 分.
).0(log22
1)( 2 >+−= xxxxxh a
.ln
12)( axxxh +−=′
),0()( +∞在xh
),0(0
ln
12 +∞≥+− 在
ax
x
.ln
120ln
12,0 2
axxaxxx −≥−⇔≥+−> 时
),0(1)1(2 22 +∞−−=− 在xxx −
.ln
11,ln
11 aa
≤−≥− 即
)1ln
1.0ln
1,10(1 矛盾这与则若 ≥<<<>
aaaa
.1ln ≤a
)0(ln
1ln2ln
ln
12)(
2
>+−=+−=′ xax
axax
axxxh
2( ) ( ) ( 2ln ) 4ln 0,h x a a′ ∆ = − − ≥存在 正 零点知
1ln ≥a ).,0ln,1(0ln 这是不可能的因为 >>≤ aaa
.1ln =a
eaxxh ==′ 故存在正零点 ,1)(
1ln =a ,1)( =′ xxh 存在正零点
,1)(,ln)(
0
0 xxgxxg =′=
.lnln,)()(1
0
0 mn
mnxmn
mgng
x −
−=−
−=
.ln ln
n mm n m
−< −
.0lnln <+−− mnmmnm
),0(lnln)( nxxnxxnxxr ≤<+−−=
),0(,lnln)( nxxnxr ∈−=′ 当
],0()(,0)( nxrxr 在所以>′
,0)()(, =<< nrmrnm 时 .0lnln <+−− mnmmnm
mx >0
.,.lnln 0 nxmmn
mnn <<−
−> 综上
4.烟台市三月诊断性检测数学理 22.(本小题满分 14 分)
设函数 ( 为自然对数的底数).
(1)求 的极值;
( 2 ) 若 存 在 实 常 数 k 和 b , 使 得 函 数 和 对 其 定 义 域 上 的 任 意 实 数 分 别 满 足 和
,则称直线 为 和 的“隔离直线”.
试问函数 和 是否存在“隔离直线”?若存在.求出此“隔离直线”方程;若不存在,请说明理由.
解:(1)∵
∴
∴当 时, .
∵当 时 此时 递减;……………………………………3’
当 时, ,此时 递增.
∴当 时, 取极小值,其极小值为 0.…………………………………6’
(2)由(1)可知,当 时, (当且仅当 时取等号).
若存在 和 的“隔离直线”,则存在实常数 和 ,
使得 和 恒成立.
∵ 和 的图象在 处有公共点,因此若存在 和 的“隔离直线”,
则该直线过这个公共点 . …………………………………………………8’
设“隔离直线”方程为 ,即
由 可得 当 时恒成立.
∵
∴由 ,得 ……………………………………………………………10’
下面证明 当 时恒成立.
令 则
当 时, ;
2( ) , ( ) 2 lnh x x x e xϕ= = e
( ) ( ) ( )F x h x xϕ= −
( )f x ( )g x x ( )f x kx b≥ +
( )g x kx b≤ + :l y kx b= + ( )f x ( )g x
( )h x ( )xϕ
2( ) ( ) ( ) 2 ln ( 0)F x h x x x e x xϕ= − = − >
2 2( )( )'( ) 2 .e x e x eF x x x x
− += − =
x e= '( ) 0F x =
0 x e< < '( ) 0F x < ( )F x
x e> '( ) 0F x > ( )F x
x e= ( )F x
0x > ( ) ( )h x xϕ≥ x e=
( )h x ( )g x k b
( )h x kx b≥ + ( ) ( 0)x kx b xϕ ≤ + >
( )h x ( )g x x e= ( )h x ( )g x
( , )e e
( )y e k x e− = − .y kx e k e= + −
( ) ( ),h x kx e k e x R≥ + − ∈ 2 0x kx e k e− − + ≥ x R∈
2( 2 )k e∆ = −
0∆ ≤ 2k e=
( ) 2x ex eϕ ≤ − 0x >
( ) ( ) 2 2 ln 2 ,G x x ex e e x ex eϕ= − + = − +
2 2 ( )'( ) 2 .e e e xG x ex x
−= − =
x e= '( ) 0G x =
当 时, ,此时 递增;
当 时, 此时 递减.
∴当 时, 取极大值.其极大值为 0.
从而
即 恒成立.………………………………………………13’
∴函数 和 存在唯一的“隔离直线” ………………………14’
5.2009 届山东省德州市高三第一次练兵(理数)21.(本小题满分 12 分)
已知函数 在 是增函数, 在(0,1)为减函数.
(1)求 、 的表达式;
(2)求证:当 时,方程 有唯一解;
(3)当 时,若 在 ∈ 内恒成立,求 的取值范围.
解:(1) 依题意 ,即 , .
∵上式恒成立,∴ ① …………………………1 分
又 ,依题意 ,即 , .
∵上式恒成立,∴ ② …………………………2 分
由①②得 . …………………………3 分
∴ …………………………4 分
(2)由(1)可知,方程 ,
设 ,
令 ,并由 得 解知 ………5 分
令 由 …………………………6 分
列表分析:
(0,1) 1 (1,+∞)
- 0 +
递减 0 递增
可知 在 处有一个最小值 0, …………………………7 分
当 时, >0,
∴ 在(0,+∞)上只有一个解.
即当 x>0 时,方程 有唯一解. …………………………8 分
(3)设 , …………9 分
0 x e< < '( ) 0G x > ( )G x
x e> '( ) 0G x < ( )G x
x e= ( )G x
( ) 2 ln 2 0,G x e x ex e= − + ≤
( ) 2 ( 0)x ex e xϕ ≤ − >
( )h x ( )xϕ 2 .y ex e= −
xaxxf ln)( 2 −= ]2,1( xaxxg −=)(
)(xf )(xg
0>x 2)()( += xgxf
1−>b 2
12)(
x
bxxf −≥ x ]1,0( b
,2)( x
axxf −=′ ]2,1(,0)( ∈>′ xxf 22xa < ]2,1(∈x
2≤a
x
axg
2
1)( −=′ )1,0(,0)( ∈<′ xxg xa 2> )1,0(∈x
.2≥a
2=a
.2)(,ln2)( 2 xxxgxxxf −=−=
2)()( += xgxf .022ln22 =−+−− xxxx即
22ln2)( 2 −+−−= xxxxxh ,1122)(
xxxxh +−−=′则
0)( >′ xh ,0>x ,0)222)(1( >+++− xxxxx .1>x
,0)( <′ xh .10,0 <<> xx 解得
x
)(xh′
)(xh
)(xh 1=x
10 ≠> xx 且 )(xh
0)( =xh
2)()( += xgxf
2 '
2 3
1 2 2( ) 2ln 2 ( ) 2 2 0x x x bx x x bx x x
ϕ ϕ= − − + = − − − <则
在 为减函数 又 ………11 分
所以: 为所求范围. …………………………12 分
6.山东省实验中学 2009 届高三第三次诊断考试(数学理)22.
已知函数 (注: )
(1)若函数 在 上为增函数,求正实数 的取值范围;
(2)当 时,若直线 与函数 的图象在 上有两个不同交点,求实数 的取值范围:
(3)求证:对大于 1 的任意正整数
解:(1)因为 所以
依题意可得,对 恒成立,
所以 对 恒成立,
所以 对 恒成立, ,即
(2)当 时, 若 , , 单调递减;
若 单调递增;
故 在 处取得极小值,即最小值
又
所以要使直线 与函数 的图象在 上有两个不同交点,
实数 的取值范围应为 ,即 ;
(3)当 时,由 可知, 在 上为增函数,
当 时,令 ,则 ,故 ,
即 所以 .
故
相加可得
又因为
所以对大于 1 的任意正整书
(二)2009 年 4 月后
7.山东省滨州市 2009 年 5 月高考模拟试题(理数)20.(本题满分 12)
1( ) lnxf x xax
−= + ln 2 0.693≈
( )f x [1, )+∞ a
1a = y b= ( )y f x= 1[ ,2]2 b
1 1 1 1,ln 2 3 4n n n
> + + + +…
1( ) lnxf x ax
−= + 2
1'( ) ( 0)axf x aax
−= >
2
1[1, ). '( ) 0axx f x ax
−∀ ∈ +∞ = ≥
[1, ). 1 0x ax∀ ∈ +∞ − ≥
1[1, ),x a x
∀ ∈ +∞ ≥ max
1( )a x
≥ 1a ≥
1a = 2
1'( ) ,xf x x
−= 1[ ,1]2x∈ '( ) 0f x ≤ ( )f x
[1,2]. '( ) 0, ( )x f x f x∈ ≥
( )f x 1x = (1) 0f =
1 1( ) 1 ln 2, (2) ln 2 ,2 2f f= − = −
31 3 ln ln16( ) (2) 2ln 2 02 2 2
ef f
−− = − = >
y b= ( )y f x= 1[ ,2]2
b ( (1), (2)]f f 10,ln 2 ]2
−
1a = (1) 1( ) lnxf x xx
−= + [1, )+∞
1n >
1
nx n
= − 1x > ( ) (1) 0f x f> =
1 11( ) ln ln 01 1 1
1
n
n n nnf nn n n n
n
− −= + = − + − >− − −
−
1ln 1
n
n n
>−
2 1 3 1 4 1 1ln ,ln ,ln , ln1 2 2 3 3 4 -1
n
n n
> > > >… ,
2 3 4 1 1 1 1ln ln ln ln1 2 3 -1 2 3 4
n
n n
+ + + > + + +…+… +
2 3 4 2 3 4ln ln ln ln ln( ) ln1 2 3 1 1 2 3 1
n n nn n
+ + + + = ⋅ ⋅ =− −… …
1 1 1 1,ln 2 3 4n n n
> + + + +…
( )xϕ∴ (0,1] min( ) (1) 1 2 1 0x bϕ ϕ∴ = = − + ≥ 1b > −
11 ≤<− b
已知函数
(Ⅰ)求 的单调区间;
(Ⅱ)当 时,设斜率为 的直线与函数 相交于两点
,求证: .
解:(Ⅰ)略
(Ⅱ)当 时,
以下先证 ,
所以只需证 ,即
设 ,则 .
所以在 时, 为减函数, .
即 .又 ,
∴ 成立,即 .
同理可证 .
∴ .
8.山东省济宁市 2009 年高三第二次摸底考试-理科数学 22.(本题满分 14 分)
设函数 .( 是自然对数的底数)
(Ⅰ)判断函数 零点的个数,并说明理由;
(Ⅱ)设数列 满足: ,且
①求证: ;
②比较 与 的大小.
解:(Ⅰ)
令
当 时, 在 上是增函数
2( ) ln .f x ax x= +
( )f x
0a = k ( )y f x= 1 1 2 2( , ) ( , )A x y B x y、
2 1( )x x> 1 2
1x xk
< <
0a = ( ) ln .f x x=
1
1 xk
> 2 1 2 1
2 1 2 1
ln ln 0,y y x xk x x x x
− −= = >− −
2 1
2 1 1
ln ln 1x x
x x x
− <−
2 2 1 2
1 1 1
ln 1.x x x x
x x x
−< = −
( ) ln 1( 1)t t t tϕ = − + > 1( ) 1 0 ( 1)t tt
ϕ′ = − < >
(1, )t ∈ +∞ ( )tϕ ( ) (1) 0 ( 1)t tϕ ϕ< = >
ln 1 ( 1)t t t< − > 2
1
1x
x
>
2 2
1 1
ln 1x x
x x
< − 1
1 xk
>
2
1 xk
<
1 2
1x xk
< <
( ) ( 1) , ( ) xf x e x g x e= − = e
( ) ( ) ( )H x f x g x= −
{ }na 1 (0,1)a ∈ 1( ) ( ), ,n nf a g a n N ∗
+ = ∈
0 1na< <
na 1( 1) ne a +−
( ) ( 1) xH x e e′ = − −
0( ) 0, ln( 1)H x x e′ = = −
0( , )x x−∞ ( ) 0,H x′ > ( )H x 0( , )x x−∞
当 时, 在 上是减函数 …………….2 分
从而 ………….4 分
注意到函数 在 上是增函数,
从而 从而
综上可知: 有两个零点. ………………………………………………….6 分
(Ⅱ)因为 即
所以 ………………………………………………….7 分
①下面用数学归纳法证明 . 当 时, ,不等式成立.
假设 时, 那么
即
这表明 时,不等式成立.
所以对 , ………………………………………………….10 分
②因为
考虑函数 …………………………………….12 分
从而 在 上是增函数
所以
即 …………………………………………………………14 分
9.山东省安丘、五莲、诸城、兰山四地 2009 届高三 5 月联考 22.(本题满分 14 分)
已知函数 在 上为增函数,且 ,
, .
(1)求 的取值范围;
(2)若 在 上为单调函数,求 的取值范围;
(3)设 ,若在 上至少存在一个 ,使得 成立,求 的取值范围.
解:
(1)由题意, 在 上恒成立,即
.故 在 上恒成立, ……………2 分
0( , )x x +∞ ( ) 0,H x′ < ( )H x 0( , )x x +∞
0
max 0( ) (0) ( 1) 1 ( 1)ln( 1) 2xH x H e x e e e e= = − + − = − − − +
( ) ln 1k t t t t= − + [ )1,+∞
( ) (1) 0, 1 1k t k e≥ = − >又 0( ) 0H x >
( )H x
1( ) ( ),n nf a g a+ = 1( 1) 1 na
ne a e+− + =
1
1 ( 1)1
na
na ee+ = −−
(0,1)na ∈ 1n = 1 (0,1)a ∈
n k= (0,1)ka ∈ 1
1 ( 1)1
ka
ka ee+ = −−
1 0 1 1k ka ae e e e< < ∴ < − < −
10 ( 1) 11
kaee
∴ < − <− 1 (0,1)ka + ∈
1n k= +
n N ∗∈ (0,1)na ∈
1( 1) 1na
n n ne a a e a+− − = − −
( ) 1 (0 1)xp x e x x= − − < <
( ) 1 0xp x e′ = − >
( )p x (0,1) ( ) (0) 0p x p> =
1( 1) 0n ne a a+− − >
1( 1) n ne a a+− >
1( ) lnsing x xxθ= +⋅ [ )1,+∞ (0, )θ π∈
1( ) lnmf x mx xx
−= − − m R∈
θ
( ) ( )f x g x− [ )1,∞ m
2( ) eh x x
= [ ]1,e 0x 0 0 0( ) ( ) ( )f x g x h x− > m
2
1 1( ) 0sing x x xθ
′ = − + ≥⋅ [ )1,+∞ 2
sin 1 0sin
x
x
θ
θ
⋅ − ≥⋅
(0, ), sin 0θ π θ∈ ∴ > sin 1 0xθ ⋅ − ≥ [ )1,+∞
只须 ,即 ,只有 .结合 得 .…4 分
(2)由(1),得
在 上为单调函数,
或者 在 恒成立. …………….. 6 分
等价于 即
而 . …………………………………8 分
等价于 即 在 恒成立,
而 .
综上, 的取值范围是 . ………………………………………10 分
(3)构造函数
当 时, , ,所以在 上不存在一个 ,
使得 成立.
当 时, …………12 分
因为 所以 , ,所以 在 恒成立.
故 在 上单调递增, ,只要 ,
解得
故 的取值范围是 ……………………………………………14 分
10.山东省烟台市 2009 届高考适应性练习(二)理综试题 22.(本小题满分 14 分)
数列 的各项均为正数, 为其前 项和,对于任意 ,总有 成等差数列.
(1)求数列 的通项公式;
(2)设数列 的前 项和为 ,且 ,求证:对任意实数 是常数, =2.71828…)和任意正整
数 ,总有 ;
(3)在正数数列 中, .求数列 中的最大项.
sin 1 1 0θ ⋅ − ≥ sin 1θ ≥ sin 1θ = (0, ),θ π∈
2
πθ =
( ) ( ) 2ln .mf x g x mx xx
− = − − ( ) 2
2
2( ) ( ) .mx x mf x g x x
− +′∴ − =
( ) ( )f x g x− [ )1,∞
2 2 0mx x m∴ − + ≥ 2 2 0mx x m∴ − + ≤ [ )1,∞
2 2 0mx x m− + ≥ 2(1 ) 2 ,m x x+ ≥ 2
2 ,1
xm x
≥ +
2
2 2 2, max 1 11 11
x mx x xx x
= = ∴ ≥ + + +
2 2 0mx x m∴ − + ≤ 2(1 ) 2 ,m x x+ ≤ 2
2
1
xm x
≤ + [ )1,∞
( ]2
2 0,1 , 01
x mx
∈ ≤+
m ( ] [ ),0 1,−∞ +∞
2( ) ( ) ( ) ( ), ( ) 2ln .m eF x f x g x h x F x mx xx x
= − − = − − −
0m ≤ [ ]1, , 0mx e mx x
∈ − ≤ 22ln 0ex x
− − < [ ]1,e 0x
0 0 0( ) ( ) ( )f x g x h x− >
0m >
2
2 2 2
2 2 2 2( ) .m e mx x m eF x m x x x x
− + +′ = + − + =
[ ]1, ,x e∈ 2 2 0e x− ≥ 2 0mx m+ > ( ) 0F x′ > [ ]1,e
( )F x [ ]1,e max
4( ) 4F x me e
= − − 4 4 0me e
− − >
2
4 .1
em e
> −
m 2
4 , .1
e
e
+∞ −
{ }na nS n n N ∗∈ 2, ,n n na S a
{ }na
{ }nb n nT 2
ln n
n
n
xb a
= (1, ](x e e∈ e
n 2nT <
{ }nc 1
1 ( ) ,( )n
n na c n N+ ∗
+ = ∈ { }nc
解:由已知:对于 ,总有 成立…(1)
…(2) ……………………………………1 分
(1)—(2)得
均为正数,
数列 是公差为 1 的等差数列 ………………………………………3 分
又 时, ,解得
……………………………………………………………5 分
(2)证明: 对任意实数 和任意正整数 ,总有 ……6 分
……………9 分
(3)解:由已知
, ,
易得
猜想 时, 是递减数列 ……………………………………………11 分
令 ,则
当 时, ,则 ,即
在 内为单调递减函数,
由 知
时, 是递减数列,即 是递减数列
又 , 数列 中的最大项为 …………………………14 分
三、2010 年模拟试题
1.山东临沂罗庄补习学校数学资料
n N ∗∈ 22 n n nS a a= +
2
1 1 12 ( 2)n n nS a a n− − −∴ = + ≥
2 2
1 12 n n n n na a a a a− −∴ = + − −
1 1 1( )( )n n n n n na a a a a a− − −∴ + = + −
1,n na a − 1 1( 2)n na a n−∴ − = ≥
∴ { }na
1n = 2
1 1 12S a a= + 1 1a =
( )na n n N ∗∴ = ∈
( ]1,x e∈ n 2 2
ln 1n
n
n
xb a n
= ≤
2 2 2
1 1 1 1 1 1... 1 ...1 2 1 2 2 3 ( 1)nT n n n
∴ ≤ + + + < + + + +⋅ ⋅ − ⋅
1 1 1 1 1 11 (1 ) ( ) ... 2 22 2 3 1n n n
= + − + − + + − = − < −
2
2 1 12 2a c c= = ⇒ =
3 3
3 2 23 3a c c= = ⇒ = 4 4
4 3 34 4 2a c c= = ⇒ = =
5 5
5 4 45 5a c c= = ⇒ =
1 2 2 3 4, ......c c c c c< > > >
2n ≥ { }nc
ln( ) xf x x
= 2 2
1 ln 1 ln( )
x x xxf x x x
⋅ − −′ = =
∴ 3x ≥ ln 1x > 1 ln 0x− < ( ) 0f x′ <
∴ ( )f x [ )3,+∞
1
1
n
n na c +
+ = ln( 1)ln 1n
nc n
+= +
2n∴ ≥ { }ln nc { }nc
1 2c c< ∴ { }nc 3
2 3c =
已知
(1)求函数 的极值点;
(2)若函数 在 上有零点,求 的最小值;
(3)证明:当 时,有 成立;
(4)若 ,试问数列 中是否存在 ?若存在,求出所有相等的两项;若不存在,
请说明理由.( 为自然对数的底数).
解:(1)由题意, 的定义域为 ……………1 分
……………………………………………………2 分
函数 的单调递增区间为 和 , 的单调递减区间为 ,
所以 为 的极大值点, ………………………………………………3 分
为 的极小值点, ………………………………………………4 分
(2) 在 上的最小值为
且
在 上没有零点,……………………………………………5 分
函数 在 上有零点,并考虑到 在 单调递增且在 单调递减,故只须 且
即可,……………………………………………6 分
易验证
当 时均有 所以函数 在 上有零点,
即函数 在 上有零点, 的最大值为 ……………9 分
(3)证明:当 时,不等式
即为:
构造函数 则
所以函数 在 上是减函数,因而 时,
即: 时, 成立,所以当 时, 成立;…11 分
23( ) ln 2, ( ) .8f x x x g x x= + + =
( ) ( ) 2 ( )F x f x g x= − ⋅
( ) ( ) 2 ( )F x f x g x= − ⋅ ), ( )te t Z +∞ ∈ t
0x > [ ] 1
( )1 ( ) g xg x e+ <
1
( 1)( ) ( )g n
nb g n n N ∗+= ∈ { }nb ( )n mb b m n= ≠
e
23( ) ln 2 28F x x x x= + + − (0, )+∞
(3 2)( 2)( ) 4
x xF x x
− −′ =
∴ ( )F x 20, 3
[ )2,+∞ ( )F x 2 ,23
2
3x = ( )F x
2x = ( )F x
( )F x 2 ,3x ∈ +∞ (2)F
23 ln 4 1(2) 2 4 2 ln 2 08 2F
−= × − + + = >
( )F x∴ 2 ,3
+∞
∴ ( )F x ),te +∞ ( )F x 20, 3
2 ,23
2
3
te < ( ) 0F t ≤
1 2 1 2 2
2
3 1 3( ) 1 2 0, ( ) 2 0,8 8F e e e F e ee
− − − − − = ⋅ + − > = ⋅ − <
2,t t Z≤ ∈ ( ) 0,tF e < ( )F x )1, ( )te e t Z− ∈
( )F x ), ( )te t Z +∞ ∈ t∴ 2−
0x > [ ] 1
( )1 ( ) g xg x e+ <
1 1(1 ) ln(1 ) 1 ln(1 )xx e x x xx
+ < ⇔ + < ⇔ + <
( ) ln(1 ) ( 0),h x x x x= + − > 1( ) 1 0,1 1
xh x x x
−′ = − = <+ +
( )h x (0, )+∞ 0x > ( ) (0) 0,h x h< =
0x > ln(1 )x x+ < 0x > [ ] 1
( )1 ( ) g xg x e+ <
(4)因为
令 ,得: ,结合 得: 时,
因此,当 时,有
所以当 时, ,即 ……………………………12 分
又通过比较 的大小知: ,
因为 且 时 所以若数列 中存在相等的两项,只能是 与后面的项可能相等,
又 ,所以数列 中存在唯一相等的两项,
即 . ……………………………………………………………………14 分
2.皖南八校 2010 届高三年级第二次联考 21.(本小题满分 13 分)
在数列 中,
(I)求证:数列 为等差数列;
(II)若 m 为正整数,当 时,求证: .
解:(I)由 变形得:
故数列 是以 为首项,1 为公差的等差数列…………(5 分)
(II)(法一)由(I)得
…………(7 分)
令
当
又
1 ( 1)( 2) 1
11
( 1)( 2) 2 2 2 2
( 1) 1 1 ( 1) 3( 1), (1 )
n n n
nnn
n n n n
n
b n n e n nb n b n n n n n
+ + +
++
+ + +
+ + + += = = ⋅ + < <
2
3( 1) 1n
n
+ < 2 3 3 0n n− − > n N ∗∈ 4n ≥
4n ≥
( 1)( 2)
1
( 1)( 2) 1,
n n
n
n n
n
b
b
+ +
+
+ + <
4n ≥ 1n nb b +> 4 5 6 ...b b b> > >
1 2 3 4b b b b、 、 、 1 2 3 4b b b b< < <
1 1,b = 1n ≠
1
1 1,n
nb n += ≠ { }nb 2 3b b、
1 1 11
3 9 64
2 8 3 52 8 , 3 5b b b b= = = = > = { }nb
2 8b b=
{ }na 1 2a = 1
1, 2 2 ( ).n
n na a n N+
+ = + ∈
}2{ n
na
2 n m≤ ≤
1 23 1( 1)( )
n
m
n
n mm n a m
⋅ −− + ≤
1
1 22 +
+ += n
nn aa 122,122 1
1
1
1 =−+= +
+
+
+
n
n
n
n
n
n
n
n aaaa 即
}2{ n
na 12
1 =a
n
n na 2⋅=
m
mnmm
m
a
nnm m
n
m
n
n 1)2
3)(1(1)3)(1(
221 −≤+−−≤⋅+− 即
m
n
m
n
nmnfnmnf
1
)2
3()()1(,)2
3()1()(
+
⋅−=+⋅+−= 则
m
nm
nm
nf
nfnm
1
)3
2(1
)1(
)(,2 ⋅−
+−=+≥> 时
mm
mnm
11
)3
2()2
11()3
2()11( ⋅−+≥⋅−+=
2
32212
11)2
11( 1 >>−+>+−⋅+=−+
m
m
mCm m
m
m
m
1
)2
3(2
11 >−+∴
则 为递减数列.
当 m=n 时, 递减数列. (9 分)
要证: 时,
故原不等式成立. (13 分)
(法二)由(I)得
(7 分)
令
上单调递减.(9 分)
∴
也即证 ,
故原不等式成立. (13 分)
)(,1)1(
)( nfnf
nf 则>+
)1()( +> nfnf )(,2 nfnm 时当 ≥≥∴
m
mmmfxf mm 1)1()4
9(),1()4
9()2()(
11
max
−≤−−==∴
2
故只需证
2,)11()1(4
91)2
3)(1(
2
≥+=+≤−≤+− mmm
m
m
mnm mmm
n
而即证
4
9
22
1
2
122
1
2
122
12
2
)1(1211)11( 22
010
=×−+≥−+=−+=
−⋅+=⋅+⋅+≥+
mm
m
mm
mmCmCCm mmm
m
n
n na 2⋅=
m
mnmm
m
a
nnm m
n
m
n
n 1)2
3)(1(1)3)(1(
221 −≤+−−≤⋅+− 即
)12
3ln1()2
3()('),2()2
3)(1()( −⋅+−=≤≤+−=
m
xmxfmxxmxf m
x
m
x
则
],2[)(0)(',11,2 mxfxfm
xmmx 在即<∴<+−∴≤≤
m
mmmfxf mm 1)1()4
9(),1()4
9()2()(
11
max
−≤−−==∴
2
故只需证
时而 2,)11(14
9 ≥+≤ mm
m
4
9
22
1
2
122
1
2
12
2
122
)1(1211)11( 22
210
=×−+≥−+
=−+=−⋅+=⋅+⋅+≥+
m
m
mmm
mmCmCCm mmm
m