高考试题——文数（江西卷）

高考试题——文数（江西卷）

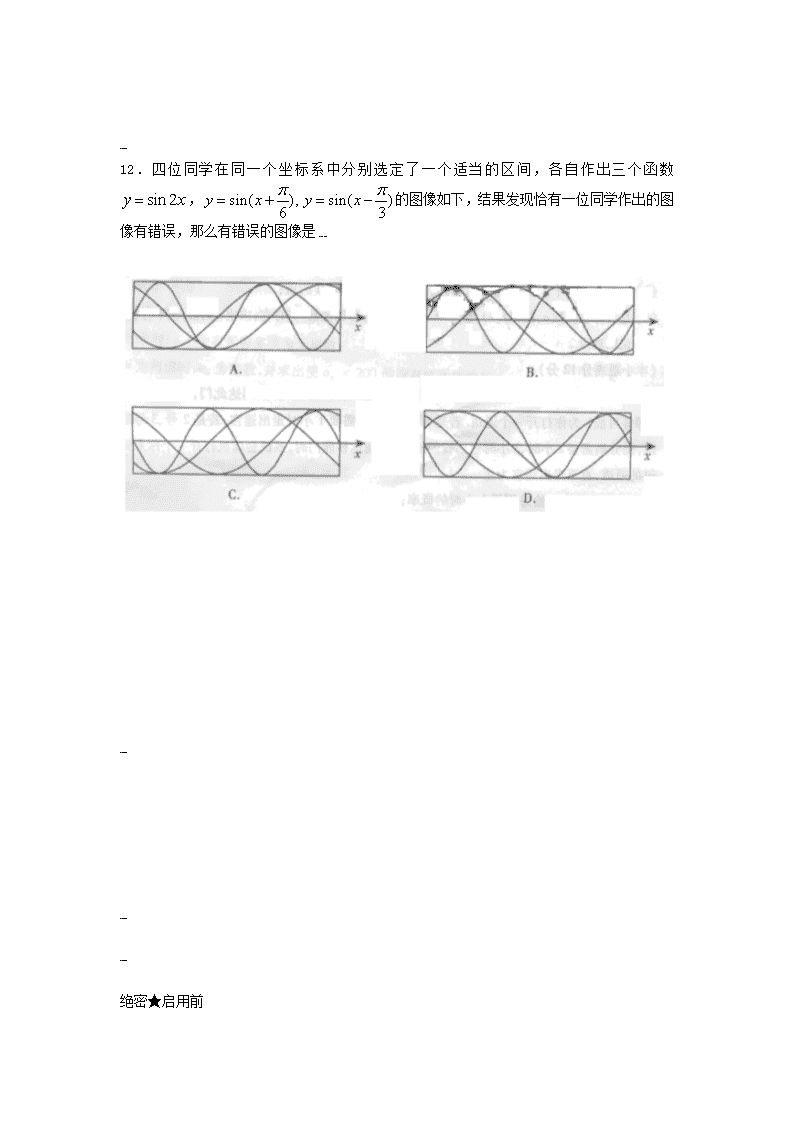
绝密★启用前 ‎2010年普通高等学校招生全国统一考试（江西卷）‎ 文科数学 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至4页，共150分．‎ 考生注意：ks5u ‎1．答题前，考生务必将自己的准考证号、姓名填写在答题卡上．考生要认真核对答题卡粘 贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．‎ ‎2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷用黑色墨水签字笔在答题卡上书写作答，在试题卷上作答，答案无效．ks5u ‎3.考试结束，监考员将试题卷、答题卡一并收回．ks5u 参考公式：‎ 如果事件互斥，那么 球的表面积公式 ‎ ‎ 如果事件相互独立，那么 其中R表示球的半径 ‎ 球的体积公式 如果事件A在一次试验中发生的概率是，那么 ‎ 次独立重复试验中事件恰好发生次的概率 其中R表示球的半径 ‎ ‎ 第Ⅰ卷 一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．对于实数，“”是“”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎2．若集合，，则 A． B．‎ C． D．‎ ‎3．展开式中项的系数为 A． B．‎720 C．120 D．‎ ‎4．若函数满足，则 A． B． C．2 D．0‎ ‎5．不等式的解集是 A． B． C． D． ‎ ‎6．函数的值域为 A． B． C． D．‎ ‎7．等比数列中，，，，则 A． B． C． D． ks5u ‎8．若函数的图像关于直线对称，则为ks5u A．1 B． C． D．任意实数 ‎9．有位同学参加某项选拔测试，每位同学能通过测试的概率都是，假设每位同学能否通过测试是相互独立的，则至少每一位同学能通过测试的概率为 A． B． C． D．‎ ‎10．直线与圆相交于两点，若，则的取值范围是 A． B． C． D．‎ ‎11．如图，是正方体的棱的中点，给出下列四个命题：‎ ‎①过点有且只有一条直线与直线都相交；‎ ‎②过点有且只有一条直线与直线都垂直；‎ ‎③过点有且只有一个平面与直线都相交；‎ ‎④过点有且只有一个平面与直线都平行．‎ 其中真命题是 A．②③④ B．①③④ C．①②④ D． ①②③‎ ks5u K#s……5&u ‎12．四位同学在同一个坐标系中分别选定了一个适当的区间，各自作出三个函数，的图像如下，结果发现恰有一位同学作出的图像有错误，那么有错误的图像是K#s……5&u K#s……5&u K#s……5&u K#s……5&u 绝密★启用前 ‎2010年普通高等学校招生全国统一考试（江西卷）‎ 文科数学 第Ⅱ卷 注意事项：‎ ‎ 第Ⅱ卷共2页，须用黑色墨水签字笔在答题卡上书写作答，在试题卷上作答，答案无效．‎ 二．填空题：本大题共4小题，每小题4分，共16分．请把答案填在答题卡上．‎ ‎13．已知向量，满足，与的夹角为60°，则在上的投影是 ．‎ ‎14．将5位志愿者分成3组，其中两组各2人，另一组1人，分赴世博会的三个不同场馆服务，不同的分配方案有 种（用数字作答）．‎ ‎15．点在双曲线的右支上，若点A到右焦点的距离等于，则 ‎ ．‎ ‎16．长方体的顶点均在同一个球面上，，，则，两点间的球面距离为 ．‎ 三．解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ 设函数．K#s……5&u ‎（1）若的两个极值点为，，且，求实数的值；K#s……5&u ‎（2）是否存在实数，使得是上的单调函数？若存在，求出的值；若不存在，说明理由．‎ ‎18．（本小题满分12分）‎ 某迷宫有三个通道，进入迷宫的每个人都要经过一扇智能门．首次到达此门，系统会随机（即等可能）为你打开一个通道．若是1号通道，则需要1小时走出迷宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门．再次到达智能门时，系统会随机打开一个你未到过的通道，直至走出迷宫为止．‎ ‎（1）求走出迷宫时恰好用了l小时的概率；‎ ‎（2）求走出迷宫的时间超过3小时的概率．‎ ‎19．（本小题满分12分）‎ 已知函数．‎ ‎（1）若，求；‎ ‎（2）若，求的取值范围．‎ ‎20．（本小题满分12分）‎ 如图，与都是边长为2的正三角形，平面平面，平面，．‎ ‎（1）求直线与平面所成角的大小；‎ ‎（2）求平面与平面所成二面角的正弦值．‎ ‎21．（本小题满分12分）‎ 如图，已知抛物线：经过椭圆：的两个焦点．‎ ‎（1）求椭圆的离心率；‎ ‎（2）设点，又，为与不在轴上的两个交点，若的重心在抛物线上，求和的方程．‎ K#s……5&u ‎22．（本小题满分14分）‎ 正实数数列中，，，且成等差数列．‎ ‎（1）证明数列中有无穷多项为无理数；‎ ‎（2）当为何值时，为整数，并求出使的所有整数项的和．‎