打印高考数学一轮总复习阶段性测试题三角函数与三角形

打印高考数学一轮总复习阶段性测试题三角函数与三角形

阶段性测试题四(三角函数与三角形) 第Ⅰ卷(选择题　共 60 分) 一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四 个选项中，只有一项是符合题目要求的．) 1．(2014·威海期中)角 α 的终边经过点 P(sin10°，－cos10°)，则 α 的可能取值 为(　　) A．10° B．80° C．－10° D．－80° [答案]　D [解析]　由条件知 tanα＝ －cos10° sin10° ＝－tan80° ＝tan(－80°)，故选 D. 2．(文)(2014·北京海淀期中)在△ABC 中，若 tanA＝－2，则 cosA＝(　　) A. 5 5 B．－ 5 5 C.2 5 5 D．－2 5 5 [答案]　B [解析]　在△ABC 中，若 tanA＝－2，则 A∈(π 2，π)， cosA＝－ 1 1＋tan2A ＝－ 1 5 ＝－ 5 5 ， 故选 B. (理)(2014·三亚市一中月考)若 tanα＝2，则 cos2α＋sin2α 的值为(　　) A．0 B.1 5 C．1 D.5 4 [答案]　B [解析]　∵tanα＝2， ∴cos2α＋sin2α＝cos2α－sin2α＋2sinαcosα sin2α＋cos2α ＝1－tan2α＋2tanα tan2α＋1 ＝1 5. 3．(文)(2014·江西临川十中期中)已知 sin(θ＋π 2)＝3 5，则 cos2θ 等于(　　) A.12 25 B．－12 25 C．－ 7 25 D. 7 25 [答案]　C [解析]　∵sin(θ＋π 2)＝cosθ＝3 5， ∴cos2θ＝2cos2θ－1＝－ 7 25. (理)(2014·枣庄市期中)化简 cos(π＋α)cos(π 2＋α)cos(11π 2 －α) cos(π－α)sin(－π－α)sin(9π 2 ＋α) 的结果是(　　) A．－1 B．1 C．tanα D．－tanα [答案]　C [解析]　原式＝ －cosα·(－sinα)·(－sinα) －cosα·sinα·cosα ＝tanα，故选 C. 4．(2014·山东省菏泽市期中)要得到 y＝sin(2x－2π 3 )的图象，只要将函数 y＝ sin(2x＋π 3)的图象向右平移(　　)个单位即可(　　) A.π 3 B．π C.2π 3 D.π 2 [答案]　D [解析]　∵sin[2(x－π 2)＋π 3]＝sin(2x－2π 3 )， ∴只需将 y＝sin(2x＋π 3)的图象向右平移π 2个单位可得到 y＝sin(2x－2π 3 )的图 象． 5．(2014·九江市七校联考)在△ABC 中，AC＝7，∠B＝2π 3 ，△ABC 的面积 S＝ 15 3 4 ，则 AB＝(　　) A．5 或 3 B．5 C．3 D．5 或 6 [答案]　A [解析]　设 AB＝x，BC＝y，则 x>0，y>0， 由条件得，Error!即Error! 则Error!或Error!∴AB＝3 或 5. 6．(2014·山东省菏泽市期中)已知弧度数为 2 的圆心角所对的弦长也是 2，则 这个圆心角所对的弧长是(　　) A．2 B．2sin1 C．2sin－11 D．sin2 [答案]　C [解析]　设圆半径为 R，由条件知 sin1＝1 R， ∴R＝ 1 sin1，∴l＝2R＝ 2 sin1，故选 C. 7．(文)(2014·辽宁师大附中期中)在△ABC 中，角 A、B 均为锐角，且 cosA>sinB，则△ABC 的形状是(　　) A．直角三角形 B．锐角三角形 C．钝角三角形 D．等腰三角形 [答案]　C [解析]　∵cosA＝sin(π 2－A)>sinB,0<π 2－A<π 2，0B，∴A＋B<π 2，∴ C>π 2，故选 C. (理)(2014·安徽程集中学期中)在△ABC 中，“sin(A－B)cosB＋cos(A－ B)sinB≥1”是“△ABC 是直角三角形”的(　　) A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 [答案]　A [解析]　由条件式得 sinA≥1，∴sinA＝1，∴A 为直角，但△ABC 为直角三角 形时，不一定 A 为直角，故选 A. 8．(2014·浙江省五校联考)函数 y＝2sin(π 4－x 2)sin(π 4＋x 2)的图象的一条对称轴为 (　　) A．x＝－π 2 B．x＝π 2 C．x＝π D．x＝3π 2 [答案]　C [解析]　y＝2sin(π 4－x 2)sin(π 4＋x 2)＝2sin(π 4－x 2)cos(π 4－x 2)＝sin(π 2－x)＝cosx，其对 称轴方程为 x＝kπ，k∈Z. 9．(文)(2014·江西白鹭洲中学期中)函数 y＝cos2x 在下列哪个区间上是减函数 (　　) A．[0，π 2] B．[π 4，3π 4 ] C．[－π 4，π 4] D．[π 2，π] [答案]　A [解析]　由 2kπ≤2x≤2kπ＋π 得 kπ≤x≤kπ＋π 2(k∈Z)，令 k＝0 知选 A. (理)(2014·福州市八县联考)已知 ω>0，函数 f(x)＝sin(ωx＋π 4)在(π 2，π)上单调递 减，则 ω 的取值范围是(　　) A．[1 2，5 4] B．[1 2，3 4] C．(0，1 2] D．(0,2] [答案]　A [解析]　由 2kπ＋π 2≤ωx＋π 4≤2kπ＋3π 2 及 ω>0 得， 2kπ ω ＋ π 4ω≤x≤2kπ ω ＋5π 4ω，k∈Z. ∵f(x)在(π 2，π)上单调递减， ∴(π 2，π)⊆[2kπ ω ＋ π 4ω，2kπ ω ＋5π 4ω]， ∴k＝0，Error!∴1 2≤ω≤5 4，故选 A. 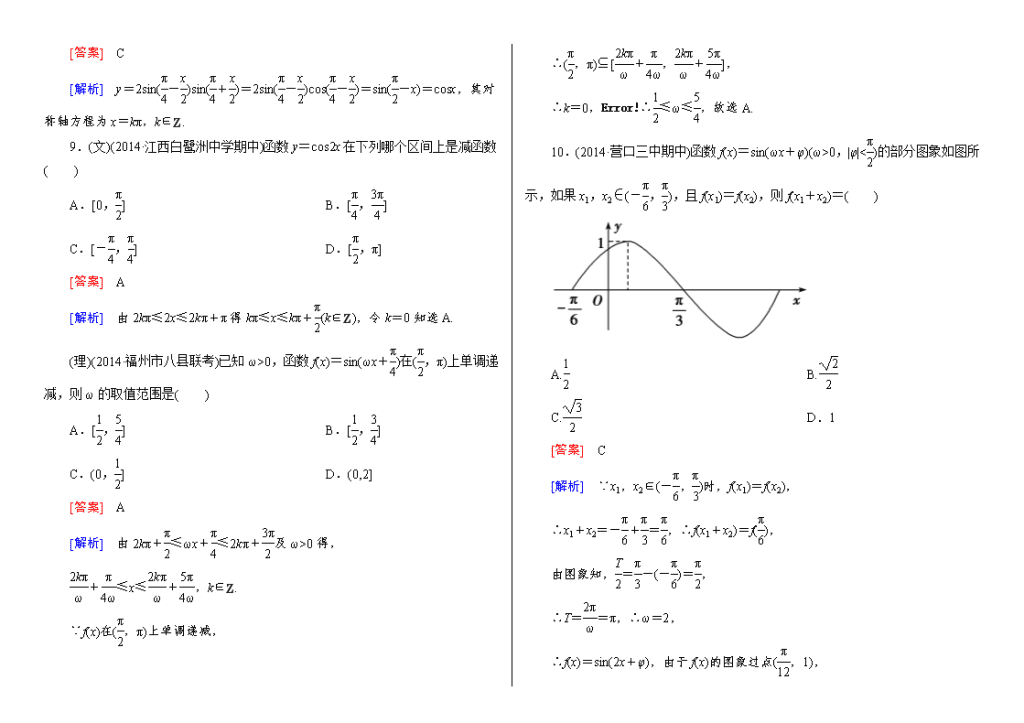10．(2014·营口三中期中)函数 f(x)＝sin(ωx＋φ)(ω>0，|φ|<π 2)的部分图象如图所 示，如果 x1，x2∈(－π 6，π 3)，且 f(x1)＝f(x2)，则 f(x1＋x2)＝(　　) A.1 2 B. 2 2 C. 3 2 D．1 [答案]　C [解析]　∵x1，x2∈(－π 6，π 3)时，f(x1)＝f(x2)， ∴x1＋x2＝－π 6＋π 3＝π 6，∴f(x1＋x2)＝f(π 6)， 由图象知，T 2＝π 3－(－π 6)＝π 2， ∴T＝2π ω＝π，∴ω＝2， ∴f(x)＝sin(2x＋φ)，由于 f(x)的图象过点( π 12，1)， ∴sin(π 6＋φ)＝1，∴φ＝π 3， ∴f(π 6)＝sin(2×π 6＋π 3)＝sin2π 3 ＝ 3 2 ，故选 C. 11．(2014·哈六中期中) 2sin225°－1 sin20°cos20°的值为(　　) A．－1 B．－2 C．1 D．2 [答案]　B [解析]　原式＝ －cos50° 1 2sin40° ＝－2. 12．(文)(2014·威海期中)函数 f(x)＝sinx＋cos2x 的图象为(　　) [答案]　B [解析]　f(0)＝sin0＋cos0＝1，排除 A、D；f(－π)＝sin(－π)＋cos(－2π)＝1， 排除 C，故选 B. (理)(2014·山东省菏泽市期中)函数 f(x)＝2x－tanx 在(－π 2，π 2)上的图象大致为 (　　) [答案]　C [解析]　∵f(－x)＝－2x－tan(－x)＝－(2x－tanx)＝－f(x)， ∴f(x)为奇函数，排除 A、B； f ′(x)＝(2x－sinx cosx)′＝2－ 1 cos2x， 令 f ′(x)≥0 得，cos2x≥1 2， ∴cosx≥ 2 2 或 cosx≤－ 2 2 ， ∵x∈(－π 2，π 2)，∴－π 4≤x≤π 4，故选 C. 第Ⅱ卷(非选择题　共 90 分) 二、填空题(本大题共 4 个小题，每小题 4 分，共 16 分，把正确答案填在题中 横线上．) 13．(2014·华安、连城、永安、漳平、泉港一中、龙海二中六校联考)在△ABC 中，三边 a、b、c 所对的角分别为 A、B、C，若 a2＋b2－c2＋ 2ab＝0，则角 C 的 大小为________． [答案]　135° [解析]　∵a2＋b2－c2＋ 2ab＝0， ∴cosC＝a2＋b2－c2 2ab ＝－ 2 2 ， ∵0°0，b>0，∴a＋b＝5. 20．(本小题满分 12 分)(文)(2014·马鞍山二中期中)已知 A，B，C 的坐标分别 为 A(3,0)，B(0,3)，C(cosα，sinα)，α∈(π 2，3π 2 )． (1)若|AC → |＝|BC → |，求角 α 的值； (2)若AC → ·BC → ＝－1，求2sin2α＋sin2α 1＋tanα 的值． [解析]　(1)∵AC → ＝(cosα－3，sinα)，BC → ＝(cosα，sinα－3)， ∴AC → 2＝(cosα－3)2＋sin2α＝10－6cosα， BC → 2＝cos2α＋(sinα－3)2＝10－6sinα， 由|AC → |＝|BC → |，可得 AC → 2＝BC → 2， 即 10－6cosα＝10－6sinα，得 sinα＝cosα. 又∵α∈(π 2，3π 2 )，∴α＝5π 4 . (2)由AC → ·BC → ＝－1，得(cosα－3)cosα＋sinα(sinα－3)＝－1，∴sinα＋cosα＝2 3.① 又2sin2α＋sin2α 1＋tanα ＝2sin2α＋2sinαcosα 1＋sinα cosα ＝2sinαcosα. 由①式两边分别平方，得 1＋2sinαcosα＝4 9， ∴2sinαcosα＝－5 9.∴2sin2α＋sin2α 1＋tanα ＝－5 9. (理)(2014·辽宁师大附中期中)已知向量 a＝(2sinx，sinx－cosx)，b＝(cosx， 3 (cosx＋sinx))，函数 f(x)＝a·b＋1. (1)当 x∈[π 4，π 2]时，求 f(x)的最大值和最小值； (2)求 f(x)的单调区间． [解析]　(1)f(x)＝sin2x－ 3cos2x＋1＝2sin(2x－π 3)＋1. ∵π 4≤x≤π 2，∴π 2≤2x≤π，∴π 6≤2x－π 3≤2π 3 ， ∴1 2≤sin(2x－π 3)≤1，∴1≤2sin(2x－π 3)≤2， 于是 2≤2sin(2x－π 3)＋1≤3， ∴f(x)的最大值是 3，最小值是 2. (2)由 2kπ－π 2≤2x－π 3≤2kπ＋π 2，k∈Z 得 2kπ－π 6≤2x≤2kπ＋5π 6 ，k∈Z， ∴kπ－ π 12≤x≤kπ＋5π 12，k∈Z， 即 f(x)的单调递增区间为[kπ－ π 12，kπ＋5π 12]，k∈Z， 同理由 2kπ＋π 2≤2x－π 3≤2kπ＋3π 2 ，k∈Z 得， f(x)的单调递减区间为[kπ＋5π 12，kπ＋11π 12 ]，k∈Z. 21．(本小题满分 12 分)(2014·马鞍山二中期中)如图 A、B 是海面上位于东西方 向相距 5(3＋ 3)n mile 的两个观测点，现位于 A 点北偏东 45°，B 点北偏西 60°的 D 点有一艘轮船发出求救信号，位于 B 点南偏西 60°且与 B 点相距 20 3n mile 的 C 点的救援船立即前往营救，其航行速度为 30n mile/h，该救援船到达 D 点需要多 长时间？ [解析]　由题意知 AB＝5(3＋ 3)n mile，∠DBA＝90°－60°＝30°，∠DAB＝90° －45°＝45°， ∴∠ADB＝180°－(45°＋30°)＝105°， 在△DAB 中，由正弦定理得， DB sin∠DAB＝ AB sin∠ADB ∴DB＝AB·sin∠DAB sin∠ADB ＝5(3＋ 3)·sin45° sin105° ＝ 5(3＋ 3)·sin45° sin45°·cos60°＋sin60°·cos45° ＝5 3( 3＋1) 3＋1 2 ＝10 3(n mile)． 又∠DBC＝∠DBA＋∠ABC＝30°＋(90°－60°)＝60°， BC＝20 3(n mile)， 在△DBC 中，由余弦定理得， CD2＝BD2＋BC2－2BD·BC·cos∠DBC ＝300＋1200－2×10 3×20 3×1 2＝900， ∴CD＝30(n mile)，则需要的时间 t＝30 30＝1(h)． 答：救援船到达 D 点需要 1h. 22．(本小题满分 14 分)(文)(2014·安徽程集中学期中)已知函数 f(x)＝Acos(ωx＋ φ)(A>0，ω>0,0<φ<π 2)的图象过点(0，1 2)，最小正周期为2π 3 ，且最小值为－1. (1)求函数 f(x)的解析式； (2)若 x∈[π 6，m]，f(x)的值域是[－1，－ 3 2 ]，求 m 的取值范围． [解析]　(1)由函数的最小值为－1，可得 A＝1，因为最小正周期为2π 3 ，所以 ω ＝3.可得 f(x)＝cos(3x＋φ)， 又因为函数的图象过点(0，1 2)，所以 cosφ＝1 2，而 0<φ<π 2，所以 φ＝π 3，故 f(x)＝ cos(3x＋π 3)． (2)由 x∈[π 6，m]，可知5π 6 ≤3x＋π 3≤3m＋π 3，因为 f(π 6)＝cos5π 6 ＝－ 3 2 ，且 cosπ ＝－1，cos7π 6 ＝－ 3 2 ， 由余弦曲线的性质知，π≤3m＋π 3≤7π 6 ，得2π 9 ≤m≤5π 18，即 m∈[2π 9 ，5π 18]． (理)(2014·浙江省五校联考)已知函数 f(x)＝( 3sinωx＋cosωx)cosωx－1 2，其中 ω>0，f(x)的最小正周期为 4π. (1)求函数 f(x)的单调递增区间； (2)在△ABC 中，角 A、B、C 的对边分别是 a、b、c，且满足(2a－c)cosB＝ bcosC，求函数 f(A)的取值范围． [解析]　f(x)＝ 3sinωx·cosωx＋cos2ωx－1 2 ＝ 3 2 sin2ωx＋1 2cos2ωx＝sin(2ωx＋π 6)． (1)∵2π 2ω＝4π，∴ω＝1 4，f(x)＝sin(x 2＋π 6)． 由 2kπ－π 2≤x 2＋π 6≤2kπ＋π 2(k∈Z)得： 4kπ－4π 3 ≤x≤4kπ＋2π 3 . ∴f(x)的单调递增区间是[4kπ－4π 3 ，4kπ＋2π 3 ](k∈Z)． (2)由正弦定理得，(2sinA－sinC)cosB＝sinB·cosC， ∴2sinAcosB＝sin(B＋C)， ∵sin(B＋C)＝sin(π－A)＝sinA>0， ∴cosB＝1 2，∵0sinB，则△ABC 的形状是(　　) A．直角三角形 B．锐角三角形 C．钝角三角形 D．等腰三角形 (理)(2014·安徽程集中学期中)在△ABC 中，“sin(A－B)cosB＋cos(A－ B)sinB≥1”是“△ABC 是直角三角形”的(　　) A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 8．(2014·浙江省五校联考)函数 y＝2sin(π 4－x 2)sin(π 4＋x 2)的图象的一条对称轴为 (　　) A．x＝－π 2 B．x＝π 2 C．x＝π D．x＝3π 2 9．(文)(2014·江西白鹭洲中学期中)函数 y＝cos2x 在下列哪个区间上是减函数 (　　) A．[0，π 2] B．[π 4，3π 4 ] C．[－π 4，π 4] D．[π 2，π] (理)(2014·福州市八县联考)已知 ω>0，函数 f(x)＝sin(ωx＋π 4)在(π 2，π)上单调递 减，则 ω 的取值范围是(　　) A．[1 2，5 4] B．[1 2，3 4] C．(0，1 2] D．(0,2] 10．(2014·营口三中期中)函数 f(x)＝sin(ωx＋φ)(ω>0，|φ|<π 2)的部分图象如图所 示，如果 x1，x2∈(－π 6，π 3)，且 f(x1)＝f(x2)，则 f(x1＋x2)＝(　　) A.1 2 B. 2 2 C. 3 2 D．1 11．(2014·哈六中期中) 2sin225°－1 sin20°cos20°的值为(　　) A．－1 B．－2 C．1 D．2 12．(文)(2014·威海期中)函数 f(x)＝sinx＋cos2x 的图象为(　　) (理)(2014·山东省菏泽市期中)函数 f(x)＝2x－tanx 在(－π 2，π 2)上的图象大致为 (　　) 第Ⅱ卷(非选择题　共 90 分) 二、填空题(本大题共 4 个小题，每小题 4 分，共 16 分，把正确答案填在题中 横线上．) 13．(2014·华安、连城、永安、漳平、泉港一中、龙海二中六校联考)在△ABC 中，三边 a、b、c 所对的角分别为 A、B、C，若 a2＋b2－c2＋ 2ab＝0，则角 C 的 大小为________． 14．(文)(2014·甘肃临夏中学期中)函数 f(x)＝3sin(2x－π 3)的图象为 C，则如下结 论中正确的序号是________． ①图象 C 关于直线 x＝11 12π 对称； ②图象 C 关于点(2π 3 ，0)对称； ③函数 f(x)在区间(－ π 12，5π 12)内是增函数； ④由 y＝3sin2x 的图象向右平移π 3个单位长度可以得到图象 C. (理)(2014·威海期中)将函数 y＝sin(x－π 3)，x∈[0,2π]的图象上各点的纵坐标不变 横坐标伸长到原来的 2 倍，再向左平移π 6个单位，所得函数的单调递增区间为 ____________． 15．(文)(2014·吉林省实验中学一模)设 α 为锐角，若 cos(α＋π 6)＝4 5，则 sin(2α＋ π 3)＝________. (理)(2014·吉林延边州质检)设△ABC 的三个内角 A、B、C 所对的三边分别为 a、b、c，若△ABC 的面积为 S＝a2－(b－c)2，则 sinA 1－cosA＝________. 16．(2014·浙江省五校联考)已知 O(0,0)，A(cosα，sinα)，B(cosβ，sinβ)， C(cosγ，sinγ)，若 kOA → ＋(2－k)OB → ＋OC → ＝0(00，ω>0,0<φ<π 2)的图象过点(0，1 2)，最小正周期为2π 3 ，且最小值为－1. (1)求函数 f(x)的解析式； (2)若 x∈[π 6，m]，f(x)的值域是[－1，－ 3 2 ]，求 m 的取值范围． (理)(2014·浙江省五校联考)已知函数 f(x)＝( 3sinωx＋cosωx)cosωx－1 2，其中 ω>0，f(x)的最小正周期为 4π. (1)求函数 f(x)的单调递增区间； (2)在△ABC 中，角 A、B、C 的对边分别是 a、b、c，且满足(2a－c)cosB＝ bcosC，求函数 f(A)的取值范围．