高考数学模拟题及答案解析

高考数学模拟题及答案解析

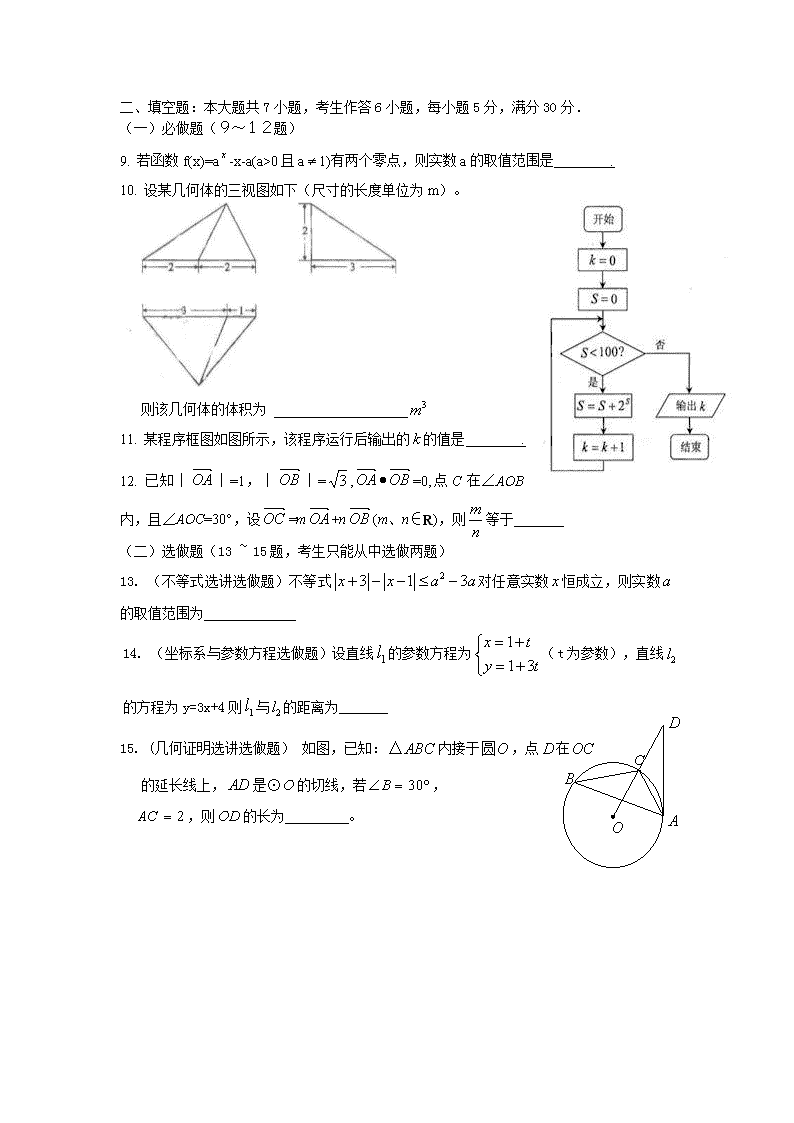
三轮复习精编模拟套题（七）‎ A. 选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 定义集合运算：．设 ‎，则集合的所有元素之和为（ ）‎ A．0；B．2；C．3；D．6‎ ‎2. 复数等于（ ）‎ A.1+i B.－1+i C.1－i D.－1－i ‎3. 把曲线ycosx+2y－1=0先沿x轴向右平移个单位，再沿y轴向下平移1个单位，得到的曲线方程是（ ）‎ A.（1－y）sinx+2y－3=0 B.（y－1）sinx+2y－3=0‎ C.（y+1）sinx+2y+1=0 D.－(y+1)sinx+2y+1=0‎ ‎4. 在区间上随机取一个数,的值介于0到之间的概率为（ ）‎ A． B． C． D． ‎ ‎5. 等差数列的前n项和为，且 =6，=4， 则公差d等于 A．1 B C.- 2 D 3‎ ‎6. 若a＜0，＞1，则 ( )‎ A．a＞1,b＞0 B．a＞1,b＜0 C. 0＜a＜1, b＞0 D. 0＜a＜1, b＜0‎ ‎7. 若且，则下列不等式恒成立的是 （ ） ‎ A． B． C． D． ‎ ‎8. 若函数的零点与的零点之差的绝对值不超过0.25， 则可以是 A. B. ‎ C. D. ‎ 二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．‎ ‎（一）必做题（９～１２题）‎ ‎9. 若函数f(x)=a-x-a(a>0且a1)有两个零点，则实数a的取值范围是 . ‎ ‎10. 设某几何体的三视图如下（尺寸的长度单位为m）。 ‎ ‎ 则该几何体的体积为 ‎ ‎11. 某程序框图如图所示，该程序运行后输出的的值是 . ‎ ‎12. 已知︱︱=1，︱︱=,=0,点C在∠AOB内，且∠AOC=30°，设=m+n(m、n∈R)，则等于 ‎ ‎（二）选做题（13 ~ 15题，考生只能从中选做两题）‎ ‎13. （不等式选讲选做题）不等式对任意实数恒成立，则实数的取值范围为 ‎ ‎14. （坐标系与参数方程选做题）设直线的参数方程为（t为参数），直线的方程为y=3x+4则与的距离为_______ ‎ ‎15. (几何证明选讲选做题） 如图，已知：内接于，点在 的延长线上，是⊙的切线，若，‎ ‎，则的长为 。‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤.‎ ‎16. （本题满分12分）‎ 已知函数为偶函数，且其图像上相邻的一个最高点和最低点之间的距离为。‎ ‎（1）求函数f(x)的解析式；‎ ‎（2）若 的值。‎ ‎17．（本题满分12分）‎ 某商场准备在节日期间举行促销活动，根据市场调查，该商场决定从3种服装商品、2种家电商品、4种日用商品中，选出3种商品进行促销活动。‎ ‎ （1）试求选出的3种商品中至少有一种日用商品的概率；‎ ‎ （2）商场对选出的商品采用有奖促销，即在该商品现价的基础上价格提高180元，同时允许顾客每购买1件促销商品有3次抽奖的机会，若中奖，则每次中奖都可获得奖金100元，假设顾客每次抽奖时中奖与否是等可能的，试分析此种有奖促销方案对商场是否有利。‎ ‎18. （本小题满分14分）‎ 一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.‎ ‎（Ⅰ）请画出该几何体的直观图，并求出它的体积；‎ ‎（Ⅱ）用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼？试证明你的结论；‎ 正视图 侧视图 俯视图 ‎（Ⅲ）在（Ⅱ）的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.‎ ‎19. （本小题满分14分）‎ 已知，，数列满足，， ．‎ ‎（Ⅰ）求证：数列是等比数列； ‎ ‎（Ⅱ）当n取何值时，取最大值，并求出最大值；‎ ‎（III）若对任意恒成立，求实数的取值范围．‎ ‎20. （本小题满分14分）‎ 函数 ‎（Ⅰ）若。‎ ‎（Ⅱ）的切线斜率的取值范围记为集合A，曲线连线斜率取值范围记为集合B，你认为集合A、B之间有怎样的关系，（真子集、相等），并证明你的结论。‎ ‎（Ⅲ）的图象关于轴对称。你认为三次函数的图象是否具有某种对称性，并证明你的结论。‎ ‎21. （本小题满分14分）‎ ‎ 设直线与椭圆相交于A、B两个不同的点，与x轴相交于点C，记O为坐标原点.‎ ‎ （I）证明：；‎ ‎ （II）若的面积取得最大值时的椭圆方程.‎ ‎2010三轮复习精编模拟套题（七）参考答案及详细解析 ‎1-8 DBCACDDA 9. 10. 4 11. 4 12.3 ‎ ‎13. 14. 15.4‎ 一、选择题 ‎1.答案：D ‎【解析】[解题思路]根据的定义，让在中逐一取值，让在中逐一取值，在值就是的元素 ‎[解析]：正确解答本题,必需清楚集合中的元素，显然，根据题中定义的集合运算知=，故应选择D ‎ ‎2.答案： B ‎【解析】解法一：，‎ 故（2+2i）4=26（cosπ+isinπ）=－26，1－，‎ 故.‎ 于是,‎ 所以选B.‎ 解法二：原式=‎ ‎∴应选B 解法三：2+2i的辐角主值是45°，则（2+2i）4的辐角是180°；1－i的一个辐角是－60°，则（1－i）5的辐角是－300°，所以的一个辐角是480°，它在第二象限，从而排除A、C、D，选B.‎ ‎3. 答案：C ‎【解析】将原方程整理为：y=，因为要将原曲线向右、向下分别移动个单位和1个单位，因此可得y=－1为所求方程.整理得（y+1）sinx+2y+1=0.‎ 评述：本题考查了曲线平移的基本方法及三角函数中的诱导公式.如果对平移有深刻理解，可直接化为：（y+1）cos（x－）+2（y+1）－1=0，即得C选项.‎ ‎4.答案：A ‎【解析】在区间[-1，1]上随机取一个数x,即时,要使的值介于0到之间,需使或∴或，区间长度为，由几何概型知的值介于0到之间的概率为.故选A.‎ ‎5.答案：C ‎【解析】∵且.故选C ‎ ‎6.答案：D ‎ ‎【解析】由得由得，所以选D项。‎ ‎7．答案：D ‎ ‎8.答案：A ‎【解析】的零点为x=,的零点为x=1, 的零点为x=0, 的零点为x=.现在我们来估算的零点，因为g(0)= -1,g()=1,所以g(x)的零点x(0, ),又函数的零点与的零点之差的绝对值不超过0.25，只有的零点适合，故选A。‎ A. 填空题 ‎9.答案： ‎ ‎【解析】设函数且和函数,则函数f(x)=a-x-a(a>0且a1)有两个零点, 就是函数且与函数有两个交点,由图象可知当时两函数只有一个交点,不符合,当时,因为函数的图象过点(0,1),而直线所过的点（0，a）一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是. ‎ ‎10答案：4www.xkb1.com ‎11.答案：4‎ ‎【解析】对于，而对于，则 ，后面是，不 符合条件时输出的．‎ ‎12.答案：3‎ ‎【解析】点C在AB上，且。 设A点坐标为(1，0)，B点的坐标为(0，)，C点的坐标为(x，y)=(，)，，则∴ m=，n=，=3‎ ‎13．答案：‎ ‎【解析】因为对任意x恒成立，所以 ‎14.答案：‎ ‎【解析】由题直线的普通方程为，故它与与的距离为。‎ ‎15.答案：4www .xk b1.com ‎【解析】连结，则，且由知为正三角形，所以。又因为是⊙的切线，即，所以 A. 解答题 ‎16.‎ ‎17.本小题考查随机变量的分布列、数学期望及在实际问题中的应用 解：（1）从3种服装商品、2种家电商品、4种日用商品中，选出3种商品，一共有 种不同的选法，选出的3种商品中，没有日用商品的选法有种，所以选出的3种商品中至少有一种日用商品的概率为 ……（4分）‎ ‎（2）顾客在三次抽奖中所获得的奖金总额是一随机变量ξ，其所有可能的取值为0，100，200，300。（单元：元）‎ ξ=0表示顾客在三次抽奖中都没有获奖，所以，‎ 同理可得 ‎ 于是顾客在三次抽奖中所获得的奖金总额的期望值是 ‎ …………（11分）‎ 故促销方案对商场有利。‎ ‎18. 解：（Ⅰ）该几何体的直观图如图1所示，它是有一条 侧棱垂直于底面的四棱锥. 其中底面ABCD 是边长为6的正方形，高为CC1=6，故所求 体积是 ‎ ------------------------4分 A B C D D1‎ A1‎ B1‎ C1‎ 图2‎ ‎ （Ⅱ）依题意，正方体的体积是原四棱锥体积的3倍，‎ 故用3个这样的四棱锥可以拼成一个棱长为6的 正方体，其拼法如图2所示. ------------6分 ‎ 证明:∵面ABCD、面ABB1A1、面AA1D1D为全等的 正方形，于是 ，‎ 故所拼图形成立.---8分新课标第一网 ‎（Ⅲ）以C为原点，CD、CB、CC1所在直线分别为x、y、‎ z轴建立直角坐标系（如图3），‎ ‎∵正方体棱长为6，‎ 则E（0，0，3），B1（0，6，6），A（6，6，0）.‎ A B C D D1‎ A1‎ B1‎ C1‎ E H x y z G 图3‎ 设向量n=（x，y，z），满足n⊥，n⊥，‎ 于是，解得. ---12分 ‎ 取z=2，得n=（2，-1，2）. 又（0，0，6），‎ 故平面AB1E与平面ABC所成二面角的余弦值为.------14分 ‎19. 解：（I）∵，，，‎ ‎ ∴． 即．‎ 又，可知对任何，，所以．…………2分 ‎∵，‎ ‎ ∴是以为首项，公比为的等比数列．………4分 ‎（II）由（I）可知= （）．‎ ‎ ∴．‎ ‎ ．……………………………5分 ‎ 当n=7时，，；‎ ‎ 当n<7时，，；‎ ‎ 当n>7时，，．‎ ‎∴当n=7或n=8时，取最大值，最大值为．……8分 ‎ （III）由，得 （*）‎ ‎ 依题意（*）式对任意恒成立，‎ ‎ ①当t=0时，（*）式显然不成立，因此t=0不合题意．…………9分 ‎　　　　 　②当t<0时，由，可知（）．‎ ‎　　　　　　 而当m是偶数时，因此t<0不合题意．…………10分 ‎　　　　 　③当t>0时，由（）,‎ ‎∴　∴． （）……11分 ‎　　　　　　 设 （）‎ ‎　　　　　　∵ =,‎ ‎　　　　　　∴．‎ ‎　　　　　　∴的最大值为．‎ ‎　　　　　　所以实数的取值范围是．…………………………………13分 ‎20. （Ⅰ） （1分）‎ 若时 对于 （3分）‎ 若时 ‎ 对于 故f(x)在R上单调递增 （4分）‎ 若△> 0，显然不合 综合所述， （5分）‎ ‎（Ⅱ） (6分) ‎ 证明： 有 （7分）‎ 设PQ斜率K，则 ‎ = （8分）‎ ‎ （9分）‎ ‎ 若 ‎ ‎ ‎ 得 ‎ 故 （10分）‎ ‎（Ⅲ） （11分）‎ 证明1，由 ‎ 现证 （12分）‎ 设 ‎ 则 得 ‎ ‎ 故M关于点 ‎ （14分）‎ 证明2： 设 ‎ 则把 ‎ (12分 )‎ ‎ ‎ ‎ 是奇函数的充要条件是 ‎ ‎ ‎ （14分）‎ ‎21. （I）解：依题意，直线l显然不平行于坐标轴，故 将，得 ‎ ① ………………………… 3分 由直线l与椭圆相交于两个不同的点，得 ‎，‎ 即 …………………………………………………… 5分 ‎ （II）解：设由①，得 因为，代入上式，得 ……………8分 于是，△OAB的面积 ‎ ‎ ………………11分 其中，上式取等号的条件是 ……………………12分 由 将这两组值分别代入①，均可解出 所以，△OAB的面积取得最大值的椭圆方程是 ………………14分