中考总复习专题二次函数与相似的结合

中考总复习专题二次函数与相似的结合

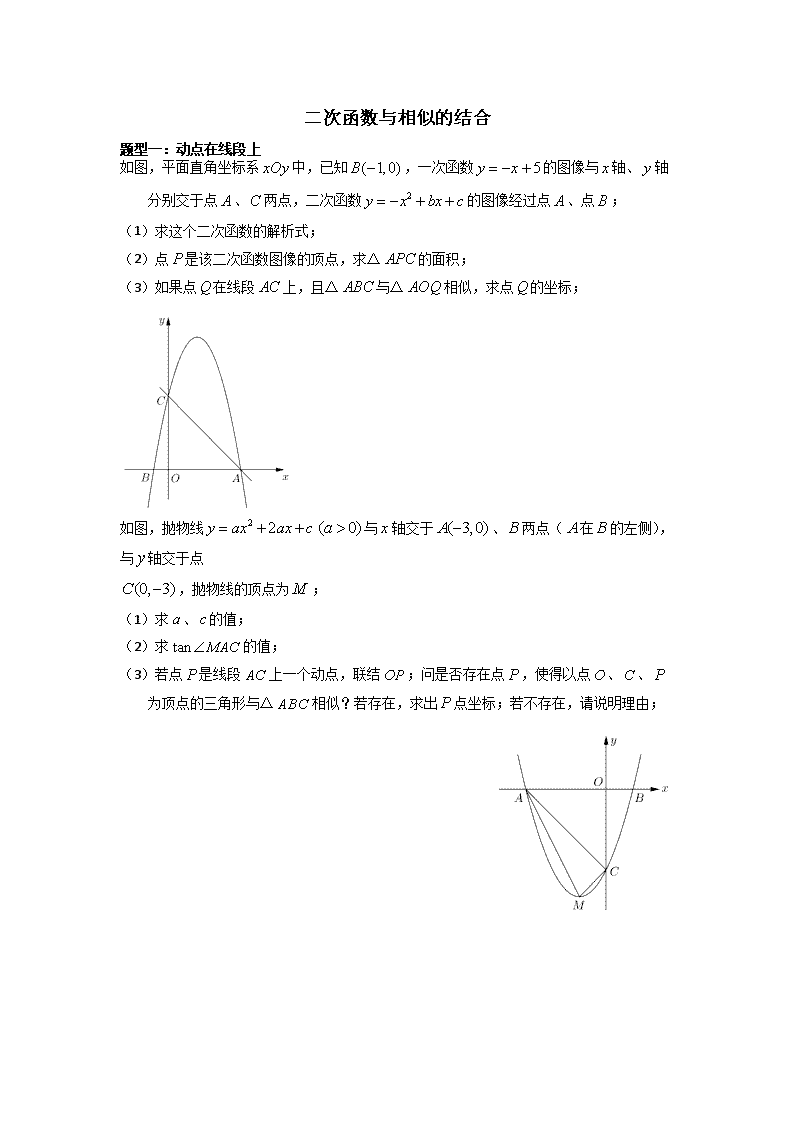
二次函数与相似的结合 题型一：动点在线段上 如图，平面直角坐标系中，已知，一次函数的图像与轴、轴分别交于点、两点，二次函数的图像经过点、点；‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）点是该二次函数图像的顶点，求△的面积；‎ ‎（3）如果点在线段上，且△与△相似，求点的坐标；‎ 如图，抛物线与轴交于、两点（在的左侧），与轴交于点 ‎，抛物线的顶点为；‎ ‎（1）求、的值；‎ ‎（2）求的值；‎ ‎（3）若点是线段上一个动点，联结；问是否存在点，使得以点、、为顶点的三角形与△相似？若存在，求出点坐标；若不存在，请说明理由；‎ 如图，已知抛物线的对称轴为直线x=1，与x轴的一个交点为A（-1，0），顶点为B. 点C（5，m）在抛物线上，直线BC交x轴于点E.‎ （1） 求抛物线的表达式及点E的坐标；‎ （2） 联结AB，求∠B的正切值；‎ x y A B E C O ‎（第24题图）‎ （3） 点G为线段AC上一点，过点G作CB的垂线交x轴于点M（位于点E右侧），‎ 当△CGM与△ABE相似时，求点M的坐标. ‎ ‎【参考答案】24．（本题满分12分，第（1）小题4分，第（2）小题3分，第（3）小题5分）‎ 解：（1）∵抛物线的对称轴为直线x=1，∴.‎ ‎∵抛物线与x轴的一个交点为A（-1，0），∴.‎ ‎∴抛物线的表达式为.………………………………………………（2分）‎ ‎∴顶点B（1，-2）.…………………………………………………………………（1分）‎ ‎∵点C（5，m）在抛物线上，∴. ∴C点坐标为（5，6）. ‎ 设直线BC的表达式为y=kx+b（k≠0），‎ 则，∴即BC的表达式为y=2x-4. ‎ ‎∴E（2,0）.……………………………………………………………………………（1分）‎ ‎（2）作CH⊥x轴，垂足为H，作BP⊥x轴，垂足为P，‎ ‎∵C（5，6），A（-1，0），∴CH=6=AH. ∴∠CAH=45°.‎ ‎∵B（1，-2），A（-1，0），∴BP=2=AP.∴∠BAP=45°.‎ ‎∴∠CAB=90°. …………………………………………………………………………（1分）‎ ‎∵CH=6=AH，CH⊥x轴，∴‎ ‎∵BP=2=AP，BP⊥x轴，∴‎ ‎∴…………………………………………………………………（2分）‎ ‎（3）∵∠CAB=90°，∴∠B+∠ACB=90°.‎ ‎∵GM⊥BC，∴∠CGM+∠ACB=90°.∴∠CGM=∠B. ………………………………（1分）‎ ‎∵△CGM与△ABE相似，∴∠BAE=∠CMG或∠BAE=∠MCG.‎ 情况1：当∠BAE=∠CMG时，‎ ‎∵∠BAE=45°，∴∠CMG=45°. ∵GM⊥BC，∴∠MCE=45°.∴∠MCE=∠EAB.‎ ‎∵∠AEB=∠CEM，∴△ABE∽△CME. ……………………………………………（1分）‎ ‎∴.即.∴EM=5. ∴M（7，0）. ……………………………（1分）‎ 情况2：当∠BAE=∠MCG时，‎ ‎∵∠BAE=∠CAM，∴∠MCG=∠CAM.∴MC=MA. ………………………………（1分）‎ 设M（x，0），∵C（5，6），A（-1，0），∴∴x=5.‎ ‎∴M（5，0）. …………………………………………………………………………（1分）‎ 题型二：动点在线段的延长线上 如图7，已知抛物线与轴交于点和点（点在点的左侧），与轴交于点，且,点是抛物线的顶点，直线和交于点。‎ （1） 求点的坐标；‎ （2） 联结，求的余切值；‎ （3） 设点在线段延长线上，如果和相似，求点的坐标。‎ ‎【答案】（1）（2）3（3）‎ ‎【解析】（1）∵抛物线与轴的交于点和点（点在点的左侧） ，‎ 与轴交于点，,且,‎ ‎∴‎ ‎∴‎ ‎（2）‎ ‎ ‎ ‎ ‎ ‎(3)由，可得,在AOC和BCD中， ,‎ ‎，‎ 又;‎ ‎;‎ 当相似时，可知;‎ 又点在线段的延长线上，,可得;‎ ‎;‎ 由题意，得直线的表达式为;设.‎ ‎,解得（舍去）‎ 点M的坐标是 题型三：动点在对称轴上 如图，抛物线经过点,，为抛物线的顶点。‎ ‎（1）求抛物线的解析式及顶点坐标；‎ ‎（2）点关于抛物线的对称点为点，联结，，求的正切值；‎ ‎（3）点是抛物线对称轴上一点，且△和△相似，求点的坐标。‎ ‎【答案】（1）；（2）（3） 或 ‎【解析】（1）∵抛物线经过点,‎ ‎ ∴ 可解得 ‎ ‎ ∴ 顶点坐标 ‎ （2）过点作垂直于交于点 ‎ ∵点与点关于对称轴对称 ‎ ∴,,平行于轴 ‎ ∵‎ ‎ ∴,‎ ‎ 在等腰直角三角形中,‎ ‎ ∴‎ ‎ 在直角三角形中,, ‎ ‎ ∴‎ ‎ ∴的正切值为 ‎ （3） 设抛物线对称轴交轴与点 ‎ ∵在直角三角形中，,‎ ‎ ∴ , ‎ ‎ ∴点在点的下方 ‎ ∴当与相似时，有下列两种情况：‎ ‎ 当 时，即 可解得 ‎ ‎ ∴‎ ‎ ‚当 时，即 可解得 ‎ ‎ ∴‎ 综上所述： 或 ‎2）动点在平移后的对称轴上 在平面直角坐标系中，点是抛物线上的一点，将此抛物线向下平移个单位以后经过点，平移后的新抛物线的顶点记为，新抛物线的对称轴和线段的交点记为。‎ （1） 求平移后得到的新抛物线的表达式，并求出点C的坐标；‎ （2） 求的正切值；‎ （3） 如果点是新抛物线对称轴上的一点，且和相似，试求点的坐标。‎ ‎【答案】（1）；（2）（3）或 ‎【解析】‎ ‎（1）∵点是抛物线上的一点，代入得：①‎ 又∵抛物线向下平移个单位以后经过点，平移后的抛物线解析式为：。‎ 代入得：②，由①②得：‎ 平移后得到的新抛物线的表达式：，顶点 （2） ‎∵、、，易得 由勾股定理逆定理得是直角三角形，‎ （3） 设抛物线对称轴与轴相交于点 ‎，，‎ 易得，‎ ‎∴点只能在对称轴点的下方，和相似，有以下两种情况：‎ ‎①，，，‎ ‎②，，，‎ 综上，或 题型四：动点在某直线上 y A O C B x ‎（第24题图）‎ ‎　如图，已知抛物线经过的三个顶点，其中点，点，轴．‎ ‎（1）求这条抛物线的解析式；‎ ‎（2）求的值；‎ ‎（3）若点D为抛物线的顶点，点E是直线AC上一点，‎ 当与相似时，求点E的坐标．‎ ‎【参考答案】24．解：（1）∵抛物线经过点和点 ‎∴……………………………………………………1分 解得………………………………………………………………2分 ‎∴这条抛物线的解析式为………………………………1分 ‎（2）过点作，垂足为 ‎，，‎ 又 是等腰直角三角形 ‎………………………………………………………1分 ‎，，点也在该抛物线上 过点作，垂足为点 ‎……………………………………………1分 又∵在Rt△中，‎ ‎∴…………………………………………………1分 ‎∴在Rt△中，……………………………1分 ‎（3）过点D作，垂足为 ‎∵点是抛物线的顶点∴………………1分 ‎∴‎ ‎∴又∵∴是等腰直角三角形 ‎∴‎ 又∵‎ ‎∴………………………………………………………1分 ‎∴当△CDE与△ABC相似时，存在以下两种情况：‎ ‎……………1分 ‎…………1分 题型五：动点在轴上 如图9，在平面直角坐标系中，顶点为的抛物线经过点和轴正半轴上的点，= 2，．‎ ‎（1）求这条抛物线的表达式；‎ ‎（2）联结，求的大小；‎ ‎（3）如果点在轴上，且△与△相似，求点的坐标．‎ 图9‎ ‎2017年青浦一模24】已知，如图8，在平面直角坐标系中，抛物线与轴正半轴交于点和点，与轴交于点，且，点是第一象限内的点，联结，△是以为斜边的等腰直角三角形.‎ （1） 求这个抛物线的表达式；‎ （2） 求点的坐标；‎ （3） 点在轴上，若以为顶点的三角形与以点为顶点的三角形相似，求点的坐标.‎ ‎【答案】（1）（2）（3）点坐标为或 ‎【解析】（1）由题意可得 代入得 ‎ （2） 过点作 为等腰直角三角形 可证四边形为正方形 ,解得在第一象限内 （3） ‎，可得为等腰直角三角形 ‎，则点在轴左侧 i. ，‎ ii. 若点在轴右侧，不存在 综上所述：点坐标为或 在平面直角坐标系中，抛物线与轴相交点和点,与轴相交于点,抛物线的顶点为点，联结,,。‎ （1） 求这条抛物线的表达式及顶点的坐标；‎ （2） 求证：‎ （3） 如果点在轴上，且在点的右侧，,求点的坐标。‎ ‎【答案】（1）；（2）略（3）‎ ‎【解析】(1)∵抛物线过点A()和点,‎ ‎ ∴将两点坐标代入解析式可得:‎ ‎ 可解得 ‎ ∴ ‎ ‎ 根据顶点公式可得 ‎ （2） 代入到求得，，所以有 可以求得：,,‎ ‎,‎ 在和中，有,‎ （3） 在OC上取一点F使得OF=OA，‎ 由（2）得B(3,0)，C(0,3)，OB=OC，∠OBC=45°，∠CBE=135°‎ OA=OF，∠AFO=45°，∠AFC=135°，∠AFC=∠CBE，又∠BCE=∠ACO，‎ ‎△AFC∽△BCE ‎,‎ ‎,‎ 题型六：动点在抛物线上 如图1，已知抛物线的方程C1： (m＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．‎ ‎（1）若抛物线C1过点M(2, 2)，求实数m的值；‎ ‎（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．‎ 图1‎ ‎【解析】（1）将M(2, 2)代入，得．解得m＝4．‎ ‎（4）①如图3，过点B作EC的平行线交抛物线于F，过点F作FF′⊥x轴于F′．‎ 由于∠BCE＝∠FBC，所以当，即时，△BCE∽△FBC．‎ 设点F的坐标为，由，得．‎ 解得x＝m＋2．所以F′(m＋2, 0)．由，得．所以．‎ 由，得．整理，得0＝16．此方程无解．‎ 图2 图3 图4‎ ‎②如图4，作∠CBF＝45°交抛物线于F，过点F作FF′⊥x轴于F′，‎ 由于∠EBC＝∠CBF，所以，即时，△BCE∽△BFC．‎ 在Rt△BFF′中，由FF′＝BF′，得．‎ 解得x＝2m．所以F′．所以BF′＝2m＋2，．‎ 由，得．解得．‎ 综合①、②，符合题意的m为．‎ ‎2）动点在直线下方的抛物线 ‎24. 如图，在平面直角坐标系中，二次函数的图像与轴交于、两点，点的坐标为，与轴交于点，点是直线下方抛物线上的任意一点；‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）联结、，并将△沿轴对折，得到四边形 ‎，如果四边形为菱形，求点的坐标；‎ ‎（3）如果点在运动过程中，能使得以、、为顶点的 三角形与△相似，请求出此时点的坐标；‎ ‎【正确答案】‎ 3） 动点在直线上方的抛物线 如图11所示，已知抛物线与轴交于A、B两点，与轴交于点C．‎ ‎（1）求A、B、C三点的坐标．‎ ‎（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．‎ ‎（3）在轴上方的抛物线上是否存在一点M，过M作MG轴 于点G，使以A、M、G三点为顶点的三角形与PCA相似．‎ 图11‎ C P B y A 若存在，请求出M点的坐标；否则，请说明理由．‎ ‎【解析:】（1）令，得 解得 令，得 ‎∴ A B C （2分）‎ ‎（2）∵OA=OB=OC= ∴BAC=ACO=BCO=‎ ‎∵AP∥CB， ∴PAB=‎ ‎ 过点P作PE轴于E，则APE为等腰直角三角形 令OE=，则PE= ∴P ‎∵点P在抛物线上 ∴ ‎ 解得，（不合题意，舍去） ∴PE= 4分）‎ ‎∴四边形ACBP的面积=AB•OC+AB•PE ‎= 6分）‎ ‎(3)． 假设存在 ‎∵PAB=BAC = ∴PAAC ‎∵MG轴于点G， ∴MGA=PAC =‎ 在Rt△AOC中，OA=OC= ∴AC=‎ G M 第28题图2‎ C B y P A 在Rt△PAE中，AE=PE= ∴AP= 7分） ‎ 设M点的横坐标为，则M ‎ ‎①点M在轴左侧时，则 ‎(ⅰ) 当AMG PCA时，有=‎ ‎∵AG=，MG=‎ 即 ‎ 解得（舍去） （舍去）‎ ‎(ⅱ) 当MAG PCA时有=‎ 即 ‎ 解得：（舍去） ‎ G M 第28题图3‎ C B y P A ‎∴M （10分）‎ ‎② 点M在轴右侧时，则 ‎ ‎(ⅰ) 当AMG PCA时有=‎ ‎∵AG=，MG= ‎ ‎∴ ‎ 解得（舍去） ‎ ‎ ∴M ‎ ‎(ⅱ) 当MAGPCA时有= ‎ 即 ‎ 解得：（舍去） ∴M ‎∴存在点M，使以A、M、G三点为顶点的三角形与PCA相似 M点的坐标为，， （13分）‎