中考数学模拟试题汇编统计与概率

中考数学模拟试题汇编统计与概率

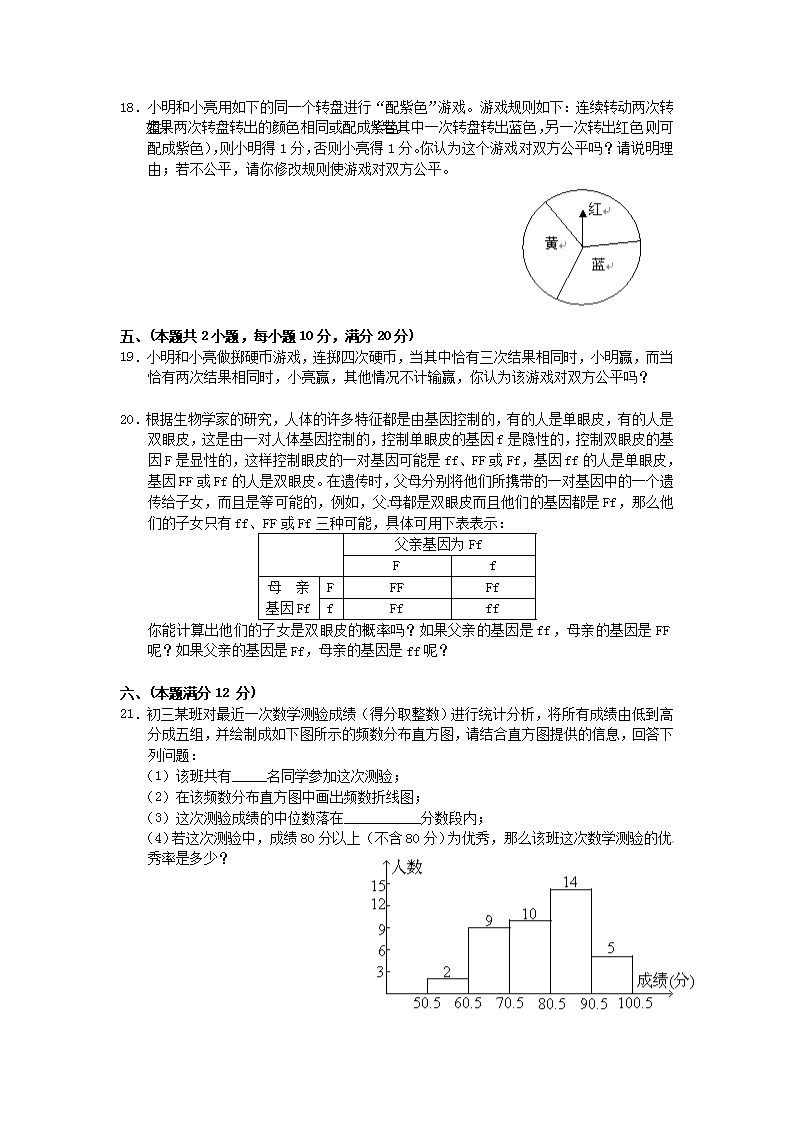
‎ 中考数学模拟试题汇编 统计与概率 一、选择题(本题共10 小题，每小题4 分，满分40分)‎ ‎1．若一组数据1，2，3，x的极差为6，则x的值是（ ）。‎ A．7 B．‎8 ‎ C．9 D．7或－3‎ ‎2．样本X1、X2、X3、X4的平均数是，方差是S2，则样本X1+3，X2+3，X3+3，X4+3的平均数和方差分别是（ ）。‎ ‎ A．+3，S2+3 B． +3， S‎2 C． ，S2+3 D． ， S2‎ ‎3．刘翔在出征北京奥运会前刻苦进行‎110米跨栏训练，教练对他20次的训练成绩进行统计分析，判断他的成绩是否稳定，则教练需要知道刘翔这20次成绩的（ ）。‎ ‎　 A、方差　　 B．平均数　　　　C．频数　　　 　D． 众数 ‎4．盒中装有5个大小相同的球，其中3个白球，2个红球，从中任意取两个球，恰好取到一个红球和一个白球的概率是（ ）。‎ A． B． C． D．‎ ‎5．如图所示的两个圆盘中，指针落在每一个数上的机会均等，‎ ‎ 那么两个指针同时落在偶数上的概率是（ ）。‎ A．； B．； C．； D． ‎ ‎6．其市气象局预报称：明天本市的降水概率为70%，这句话指的是（ ）。‎ A． 明天本市70%的时间下雨，30%的时间不下雨 ‎ B． 明天本市70%的地区下雨，30%的地区不下雨 ‎ C． 明天本市一定下雨 ‎ D． 明天本市下雨的可能性是70%‎ ‎7．某校男生中，若随机抽取若干名同学做“是否喜欢足球”的问卷调查，抽到喜欢足球的同学的概率是，这个的含义是（ ）。‎ A．只发出5份调查卷，其中三份是喜欢足球的答卷 B．在答卷中，喜欢足球的答卷与总问卷的比为3∶8‎ C．在答卷中，喜欢足球的答卷占总答卷的 D．发出100份问卷，有60份答卷是不喜欢足球 ‎8．一个袋中装有2个黄球和2个红球，任意摸出一个球后放回，再任意摸出一个球，则两次都摸到红球的概率为（ ）。‎ A． B． C． D．‎ ‎9．袋中有5个红球，有m个白球，从中任意取一个球，恰为白球的机会是，则m为（ ）。‎ ‎ A．10 B．‎16 C．20 D．18‎ ‎10．现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为、小明掷B立方体朝上的数字为来确定点P（），那么它们各掷一次所确定的点P落在已知抛物线上的概率为（ ）。‎ ‎ A． B． C． D． ‎ 二、填空题(本题共 4 小题，每小题 5 分，满分 20 分)‎ ‎11．袋中有红、黄、蓝3球，从中摸出一个，放回，共摸3次，摸到二黄一蓝的机会是 。 ‎ ‎12．晓明玩转盘游戏，当他转动如图所示的转盘，转盘停止时指针指向2的概率是 。‎ ‎13．某地区有80万人口，其中各民族所占比例如图所示，则该地区少数民族人口共有 万人。 ‎ ‎ ‎ ‎14．一只不透明的布袋中有三种小球（除颜色以外没有任何区别），分别是2 个红球，3个白球和5个黑球，每次只摸出一只小球，观察后均放回搅匀．在连续9次摸出的都是黑球的情况下，第10次摸出红球的概率是 。 ‎ 三、(本题共2小题，每小题8分，满分 16 分)‎ ‎15．某校有A、B两个餐厅，甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐。‎ ‎(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率；‎ ‎(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率。‎ ‎16．将分别标有数字2，3，5的三张质地、大小完全一样的卡片背面朝上放在桌面上。‎ ‎（1）随机抽取一张，求抽到奇数的概率；‎ ‎（2）随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的 数字，能组成哪些两位数？并求出抽取到的两位数恰好是35的概率。‎ 四、(本题共2小题，每小题8分，满分16分)‎ ‎17．甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示。游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜。‎ ‎（1）用列表法（或画树状图）求甲获胜的概率；‎ ‎（2）你认为这个游戏规则对双方公平吗？请简要说明理由。‎ ‎18．小明和小亮用如下的同一个转盘进行“配紫色”游戏。游戏规则如下：连续转动两次转盘，如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则可配成紫色），则小明得1分，否则小亮得1分。你认为这个游戏对双方公平吗？请说明理由；若不公平，请你修改规则使游戏对双方公平。‎ 五、(本题共2小题，每小题10分，满分20分)‎ ‎19．小明和小亮做掷硬币游戏，连掷四次硬币，当其中恰有三次结果相同时，小明赢，而当恰有两次结果相同时，小亮赢，其他情况不计输赢，你认为该游戏对双方公平吗？‎ ‎20．根据生物学家的研究，人体的许多特征都是由基因控制的，有的人是单眼皮，有的人是双眼皮，这是由一对人体基因控制的，控制单眼皮的基因f是隐性的，控制双眼皮的基因F是显性的，这样控制眼皮的一对基因可能是ff、FF或Ff，基因ff的人是单眼皮，基因FF或Ff的人是双眼皮。在遗传时，父母分别将他们所携带的一对基因中的一个遗传给子女，而且是等可能的，例如，父母都是双眼皮而且他们的基因都是Ff，那么他们的子女只有ff、FF或Ff三种可能，具体可用下表表示：‎ 父亲基因为Ff F f 母 亲 基因Ff F FF Ff f Ff ff 你能计算出他们的子女是双眼皮的概率吗？如果父亲的基因是ff，母亲的基因是FF呢？如果父亲的基因是Ff，母亲的基因是ff呢？‎ 六、(本题满分12 分)‎ ‎21．初三某班对最近一次数学测验成绩（得分取整数）进行统计分析，将所有成绩由低到高分成五组，并绘制成如下图所示的频数分布直方图，请结合直方图提供的信息，回答下列问题：‎ ‎（1）该班共有_____名同学参加这次测验；‎ ‎（2）在该频数分布直方图中画出频数折线图；‎ ‎（3）这次测验成绩的中位数落在___________分数段内；‎ ‎（4）若这次测验中，成绩80分以上（不含80分）为优秀，那么该班这次数学测验的优秀率是多少？‎ 七、(本题满分12分)‎ ‎22．有一种笔记本原售价为每本8元。甲商场用如下办法促销：每次购买1～8本打九折、9～16本打八五折、17～25本打八折、超过25本打七五折 乙商场用如下办法促销：‎ ‎（1）、请仿照乙商场的促销表，列出甲商场促销笔记本的购买本数与每本价格对照表；‎ ‎（2）、某学校有A、B两个班都需要购买这种笔记本。A班要8本，B班要15本。问他们到哪家商场购买花钱较少？‎ ‎（3）、设某班需购买这种笔记本的本数为x，且9≤x≤40，总花钱为y元，从最省钱的角度出发，写出y与x 的函数关系式 八、(本题满分14 分)‎ ‎23．某商场设立了一个可以自由转动的转盘(如图)，并规定：顾客购买10元以上物品就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是活动进行中的一组统计数据：‎ ‎(1)计算并完成表格：‎ 转动转盘的次数n ‎ ‎100 ‎ ‎150 ‎ ‎200 ‎ ‎500 ‎ ‎800 ‎ ‎1000 ‎ 落在“铅笔”的次数m ‎ ‎68 ‎ ‎111 ‎ ‎136 ‎ ‎345 ‎ ‎564 ‎ ‎701 ‎ 落在“铅笔”的频率 ‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　 (2)请估计，当n很大时，频率将会接近多少？‎ ‎　(3)假如你去转动该转盘一次，你获得铅笔的概率约是多少？‎ ‎　(4)在该转盘中，标有铅笔区域的扇形的圆心角大约是多少(精确到1°)？‎ 参考答案 一、1、D　　2、C　　3、A　　4、C　　5、C　　6、D 7、C 8、B ‎9、A 10、B ‎ 二、11、；12、（或0.5，50%）；13、12；14、。‎ 三、15、（1）1/4，（2）7/8；‎ ‎16、（1）抽到奇数的概率P= ；‎ ‎ （2）能组成6个不同的两位数：32, 52，23，53，25，35。 ‎ ‎ 其中恰好为35的概率为 。‎ 四、17. ⑴（法1）画树状图 由上图可知，所有等可能的结果共有12种，指针所指的两个数字之和为奇数的结果有6种。 ‎ ‎∴P（和为奇数）=0.5 ‎ ‎（法2）列表如下：‎ 盘 A 和 B 盘 转 转 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎1+5=6‎ ‎2+5=7‎ ‎3+5=8‎ ‎4+5=9‎ ‎6‎ ‎1+6=7‎ ‎2+6=8‎ ‎3+6=9‎ ‎4+6=10‎ ‎7‎ ‎1+7=8‎ ‎2+7=9‎ ‎3+7=10‎ ‎4+7=11‎ 由上表可知，所有等可能的结果共有12种，指针所指的两个数字之和为奇数的结果有6种。 ∴P（和为奇数）=0.5 ‎ ‎⑵∵P（和为奇数）=0.5‎ ‎∴P（和为偶数）=0.5 ‎ ‎∴这个游戏规则对双方是公平的。 ‎ ‎18．‎ ‎ 第二次 第一次 红 黄 蓝 红 ‎（红，红）‎ ‎（红，黄）‎ ‎（红，蓝）‎ 黄 ‎（黄，红）‎ ‎（黄，黄）‎ ‎（黄，蓝）‎ 蓝 ‎（蓝，红）‎ ‎（蓝，黄）‎ ‎（蓝，蓝）‎ 从表中可以得到：P（小明获胜）＝，P（小亮获胜）＝。‎ ‎∴小明的得分为×1＝ ， 小亮的得分为 ×1＝ 。‎ ‎∵ ＞ ，∴游戏不公平。‎ 修改规则不惟一。如若两次转出颜色相同或配成紫色，则小明得4分，否则小亮得5分。 ‎ 五、19． 概率为。‎ 若父亲的基因是ff，母亲的基因是FF时，‎ 子女的基因会出现Ff、Ff、Ff、Ff．‎ 子女出现双眼皮的概率为=100% ， ‎ 若父亲的基因是Ff，母亲的基因是ff时， ‎ 子女出现双眼皮的概率为（50%） 。 ‎ ‎20、对双方公平利用树状图.‎ 如第一次为正面，则有 其中恰好三次相同数为6,‎ 其中恰好两次相同数为6,‎ 恰有三次相同的概率为,‎ 恰有两次相同的概率为,‎ ‎∴该游戏对双方是公平的。‎ 六、21、（1）40，（2）略，（3）70.5-80.5，（4）47.5℅。‎ 七、22、（1）甲商场的促销办法列表为： ‎ 购买本数（本）‎ ‎1～8‎ ‎9～16‎ ‎17～25‎ 超过25‎ 每本价格（元）‎ ‎7.20‎ ‎6.80‎ ‎6.40‎ ‎6.00‎ ‎ （2）若A班在甲商场购买至少需57．6元，而在乙简场购买也至少需要57．6元，所以A班在甲商场购买、乙商场购买花钱一样多。‎ ‎ 若B班在甲商场购买至少需102元，而在乙商场购买至少需要96元，所以B班在乙商场购买花钱较少。 ‎ ‎ （3）由题意知，从最省钱的角度出发，可得y与x的函数关系式为：‎ ‎ ‎ ‎（若学生分别写成三种情况列出，不扣分）‎ 八、23、 （1）‎ 转动转盘的次数n ‎ ‎100 ‎ ‎150 ‎ ‎200 ‎ ‎500 ‎ ‎800 ‎ ‎1000 ‎ 停在“铅笔”的次数m ‎ ‎68 ‎ ‎111 ‎ ‎136 ‎ ‎345 ‎ ‎564 ‎ ‎701 ‎ 停在“铅笔”的频率 ‎ ‎0.68 ‎ ‎0.74 ‎ ‎0.68 ‎ ‎0.69 ‎ ‎0.705 ‎ ‎0.701 ‎ ‎　　（2）当n很大时，停在“铅笔”的频率将会接近0.7；‎ ‎　　（3）获得铅笔的概率是0.7；‎ ‎　　（4）圆心角的度数为0.7×360°＝252°。‎