- 2021-05-10 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年广西省玉林市防城港市中考试题
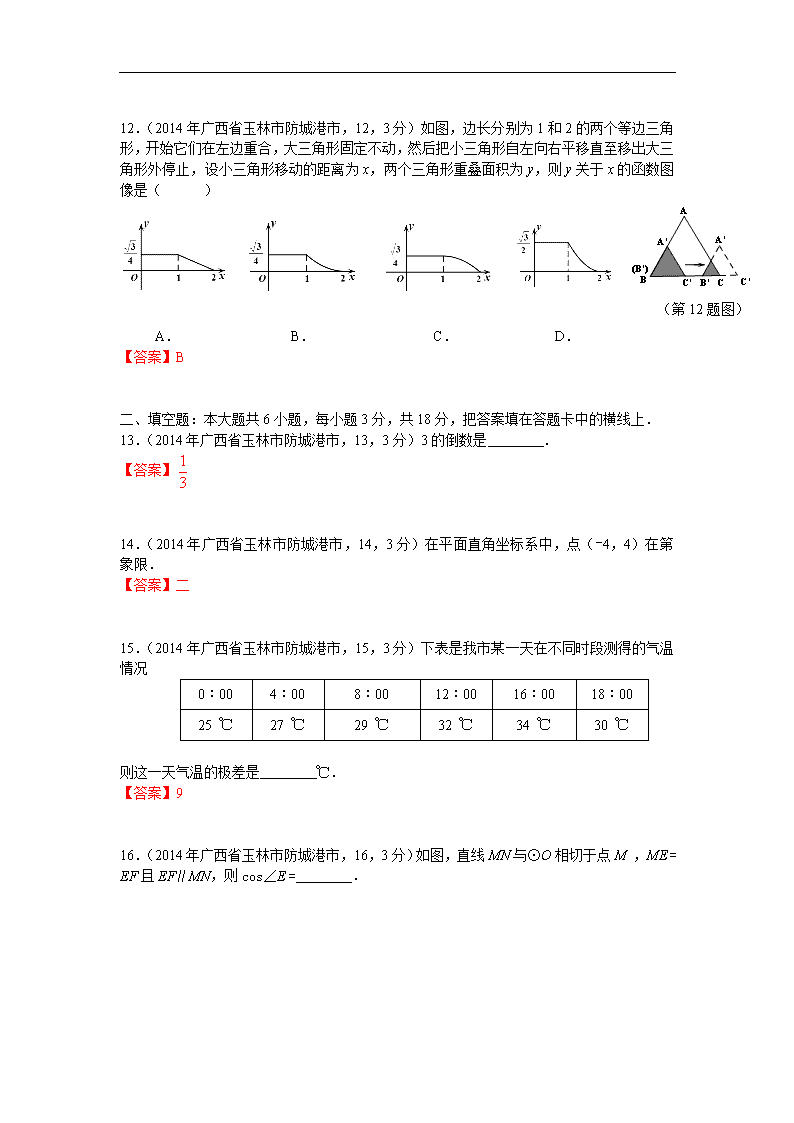
2014年广西省玉林市防城港市中考试题 数 学 (满分120分,考试时间120分钟) 一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上. 1.(2014年广西省玉林市防城港市,1,3分)下面的数与-2的和为0的是( ) A.2 B.-2 C. D. 【答案】A 2.(2014年广西省玉林市防城港市,2,3分)将6.18×10-3化为小数是( ) A.0.000618 B.0.00618 C.0.0618 D.0.618 【答案】B 3.(2014年广西省玉林市防城港市,3,3分)计算的结果是( ) A.2a5 B.6a6 C.8a6 D.8a5 【答案】C 4.(2014年广西省玉林市防城港市,4,3分)下面的多项式在实数范围内能因式分解的是( ) A.x2 + y B.x2 - y C.x2 + x + 1 D.x2 - 2x + 1 【答案】D (第5题图) 5.(2014年广西省玉林市防城港市,5,3分)右图的几何体的三视图是( ) A. B. C. D. 【答案】C 6.(2014年广西省玉林市防城港市,6,3分)下列命题是假命题的是( ) A.四个角相等的四边形是矩形 B.对角线相等的平行四边形是矩形 C.对角线垂直的四边形是菱形 D.对角线垂直的平行四边形是菱形 【答案】C 7.(2014年广西省玉林市防城港市,7,3分)△ABC与△是位似图形,且△ABC与△的位似比是1︰2,已知△ABC的面积是3,则△的面积是( ) A.3 B.6 C.9 D.12 【答案】D 8.(2014年广西省玉林市防城港市,8,3分)一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( ) A. B. C. D. 【答案】C 9.(2014年广西省玉林市防城港市,9,3分)x1,x2是关于x的一元二次方程x2 –mx + m - 2 = 0的两个实数根,是否存在实数m使成立?则正确的结论是( ) A.m = 0 时成立 B.m = 2 时成立 C.m = 0 或2时成立 D. 不存在 【答案】A 10.(2014年广西省玉林市防城港市,10,3分)在等腰△ABC中,AB = AC,其周长为20cm,则AB边的取值范围是( ) A.1cm<AB<4cm B.5cm<AB<10cm C.4cm<AB<8cm D.4cm<AB<10cm 【答案】B 11.(2014年广西省玉林市防城港市,11,3分)蜂巢的构造非常美丽、科学.右图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如右图所示,则△ABC是直角三角形的个数有( ) (第11题图) A.4个 B.6个 C.8个 D.10个 【答案】D 12.(2014年广西省玉林市防城港市,12,3分)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止,设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图像是( ) (第12题图) A. B. C. D. 【答案】B 二、填空题:本大题共6小题,每小题3分,共18分,把答案填在答题卡中的横线上. 13.(2014年广西省玉林市防城港市,13,3分)3的倒数是 . 【答案】 14.(2014年广西省玉林市防城港市,14,3分)在平面直角坐标系中,点(-4,4)在第 象限. 【答案】二 15.(2014年广西省玉林市防城港市,15,3分)下表是我市某一天在不同时段测得的气温情况 0︰00 4︰00 8︰00 12︰00 16︰00 18︰00 25 ℃ 27 ℃ 29 ℃ 32 ℃ 34 ℃ 30 ℃ 则这一天气温的极差是 ℃. 【答案】9 16.(2014年广西省玉林市防城港市,16,3分)如图,直线MN与⊙O相切于点M ,ME = EF且EF∥MN,则cos∠E = . (第16题图) 【答案】 17.(2014年广西省玉林市防城港市,17,3分)如图,在直角梯形ABCD中,AD∥BC,∠C =90°,∠A =120°,AD =2,BD平分∠ABC,则梯形ABCD的周长是 . (第17题图) 【答案】 18.(2014年广西省玉林市防城港市,18,3分)如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线和的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下的结论:① ;② 阴影部分面积是;③ 当∠AOC=90°时,;④ 若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称. 其中正确的结论是 (把所有正确的结论的序号都填上). (第18题图) 【答案】① ④ 三、解答题:本大题共8小题,满分共66分.解答过程写在答题卡上,解答应写出文字说明,证明过程或演算步骤. 19.(2014年广西省玉林市防城港市,19,6分)(满分6分)计算: 【答案】解: 原式==3 20.(2014年广西省玉林市防城港市,20,6分)(满分6分)先化简,再求值:,其中. 【答案】解: 原式= = = = 当时,原式= = 21.(2014年广西省玉林市防城港市,21,6分)(满分6分)如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC ≌ △CDE,并且△CDE可由△ABC逆时针旋转而得到。请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 . (第21题图) 【答案】解: 如图所示,点O就是所要做的旋转中心;其中旋转角度是90°. 22.(2014年广西省玉林市防城港市,22,8分)(满分8分)第一次模拟考试后,数学科陈老师把一班的数学成绩制成如右图的统计图,并给了几个信息:① 前两组的频率和是0.14;② 第一组的频率是0.02;③ 自左至右第二、三、四组的频数比为3︰9︰8.然后布置学生(也请你一起)结合统计图完成下列问题: (1)全班学生是多少人? (2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少? (3)若不少于100分可以得到A+ 等级,则小明得到A+ 的概率是多少? (第22题图) 【答案】解: (1)0.14-0.02 =0.12,6÷0.12 =50(人) 答:全班学生是50人. (2)50×0.02 =1(人), 设第三组有x人,则 ,得:x =18 ∴ 50-(1+6+18)=25(人) ∴ 答:全班成绩的优秀率是50%. (3)设第四组有y人,则 ,得:y =16 ∴ 25-16 =9(人) ∴ 答:小明得到A+ 的概率是18%. 23.(2014年广西省玉林市防城港市,23,9分)(满分9分)如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D,A分别作⊙O的切线交于点G,并与AB延长线交于点E. (1)求证:∠1=∠2; (2)已知:OF︰OB =1︰3,⊙O的半径为3,求AG的长. (第23题图) 【答案】解: (1)如图,连结OD, ∵ GE切⊙O于点D, ∴ OD⊥GE,即∠ODE =90°, ∴ ∠ODF +∠2 =90°, ∵ OC⊥AB, ∴ ∠OCF +∠CFO =90°, ∵ OC =OD, ∴ ∠ODF =∠OCF, ∴ ∠2=∠CFO(等角的余角相等) ∵ ∠CFO=∠1(对顶角相等) ∴ ∠1=∠2(等量代换) (2)∵ OB =3,OF︰OB =1︰3, ∴ OF =1, ∵ ∠1=∠2, ∴ EF = ED =x, 在Rt△ODE中,∠ODE =90°, ∴ OD2 +DE2 =OE2,即:9 + x2 =(x +1)2,得:x=4 ∴ EF = ED =4, 在Rt△ODE中,tan∠E = = ∵ AE =AO + OF + EF =3 +1 +4 =8, 又∵ GA切⊙O于点A, ∴ AE⊥AG,即∠EAG =90°, ∴ tan∠E = = = ∴ AG =6 24.(2014年广西省玉林市防城港市,24,9分)(满分9分)我市市区去年年底电动车拥有量是10万辆,为了缓解城区交通拥堵状况,今年年初,市交通部门要求我市到明年年底控制电动车拥有量不超过11.9万辆,估计每年报废的电动车数量是上一年年底电动车拥有量的10%,假定每年新增电动车数量相同,问: (1)从今年年初起每年新增电动车数量最多是多少万辆? (2)在(1)的结论下,今年年底到明年年底电动车拥有量的年增长率是多少?(结果精确到0.1%) 【答案】解: (1)设从今年年初起每年新增电动车数量是x万辆,则: 今年:10(1-10%)+ x,即(9 + x)万辆; 明年:(9 + x)(1-10%) + x,即(8.1+1.9 x)万辆; 令8.1+1.9x ≤11.9 得:x≤2 答:从今年年初起每年新增电动车数量最多是2万辆. (2)由上题可得:今年年底车辆数:9 +2 =11(万辆) 则: 答:今年年底到明年年底电动车拥有量的年增长率是8.2%. 25.(2014年广西省玉林市防城港市,25,10分)(满分10分)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P,使CP = BM,连接NP,BP. (1)求证:四边形BMNP是平行四边形; (2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由. (第25题图) 【答案】解: (1)在正方形ABCD中, AB=BC,∠ABM =∠BCP =90°, ∵ BM = CP, ∴ △ABM≌△BCP ∴ AM =BP ,∠BAM =∠CBP ∵ AM =MN, ∴ BP =MN(等量代换) ∵ ∠AMN =90°, ∴ ∠NMC +∠AMB =90°, ∵ ∠BAM +∠AMB =90°, ∴ ∠BAM =∠NMC(同角的余角相等) ∵ ∠BAM =∠CBP(已证) ∴ ∠NMC =∠CBP,∴ MN∥BP ∵ BP =MN(已证) ∴四边形BMNP是平行四边形. (2)BM = MC,其中理由如下: 作MG⊥AQ交AQ于点G(如图所示) ∵ △MCQ ∽△AMQ, ∴ ∠MQC =∠AQM,∠QMC =∠QAM , ∵ ∠BAM =∠QMC ∴ ∠BAM =∠QAM,即AM平分∠BAG, ∵ MB⊥AB,MG⊥AQ , ∴ BM =MG ∵ ∠MQC =∠AQM ,即MQ平分∠GQC, 同理可得:MC =MG ∴ BM =MC. 26.(2014年广西省玉林市防城港市,26,12分)(满分12分)给定直线l:y =kx,抛物线C:y =ax2 +bx +1. (1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值; (2)若把直线l向上平移k2 +1个单位长度得到直线l’,则无论非零实数k取何值,直线l’与抛物线C都只有一个交点. ① 求此抛物线的解析式; ② 若P是此抛物线上任一点,过P作PQ∥y轴且与直线y =2交于Q点,O为原点,求证:OP = PQ. 第26题备用图(1) 第26题备用图(2) 【答案】解: (1)当b=1时,抛物线为:y =ax2 + x +1, 令kx =ax2 + x +1,即:ax2 +(1-k)x +1=0, 由韦达定理得:x1+x2 =,因为直线l与抛物线C的两交点关于原点对称, 则x1+x2 =0,∴ =0,∴ k =1, ∴ 直线l :y =x, ∵ 抛物线顶点A在直线l 上, ∴ ,得:a =, 经检验:a =符合方程. (2)① 由题意得:直线l’解析式:y =kx +k2+1 令ax2 +bx +1 =kx +k2+1 即:ax2 +(b-k)x -k2 =0 ∵无论非零实数k取何值,直线l’与抛物线C都只有一个交点, 即不论k取任何非零实数,△=(b-k)2 +4ak2 =0恒成立, 亦即为:(1+4a)k2 -2bk +b2 =0, 令 得: ∴ 抛物线的解析式: ② 如图所示,PQ与x轴相交于点E, 不妨设点P(,),则Q(,2),OE =,PE =, ∴ PQ =2 -()=,则PQ2 ==, 而OP2 =OE2 +PE2 =, ∴ PQ2 = OP2 ,∴ OP = PQ.查看更多