遵义市2013年中考数学卷

遵义市2013年中考数学卷

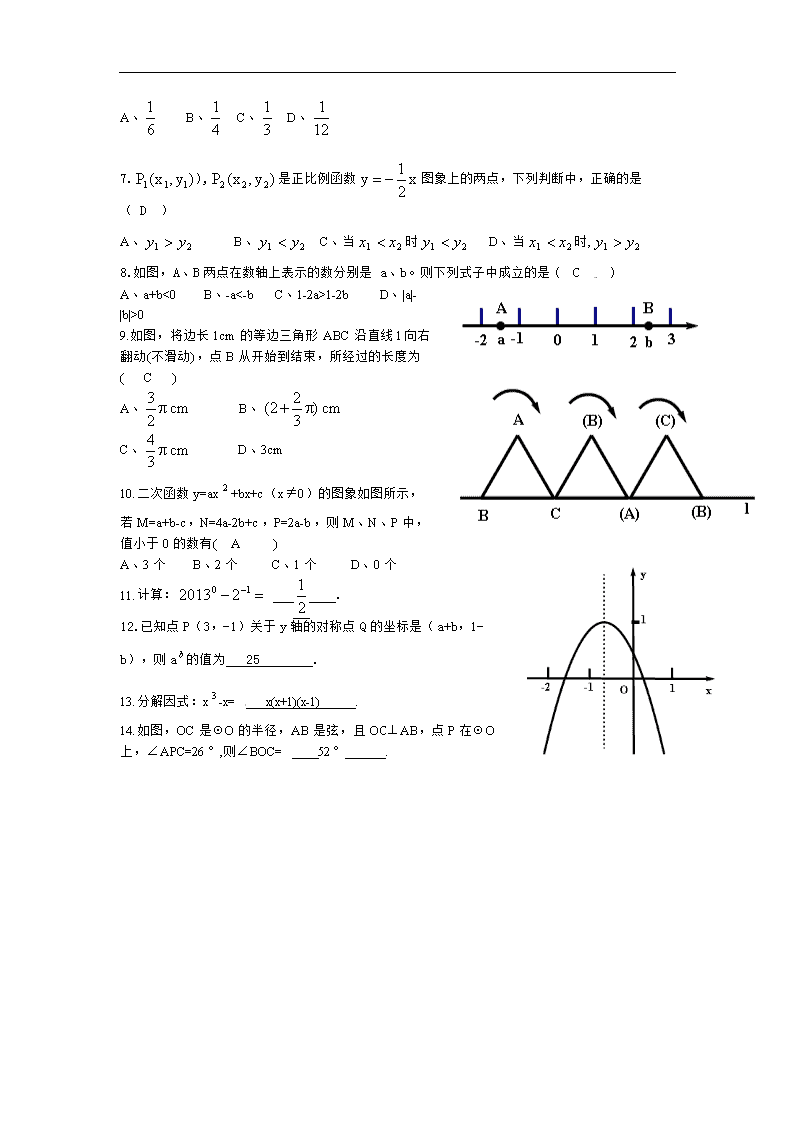
‎1.如果+‎30m表示向东走‎30m，那么向西走‎40米表示为（ B ）‎ A．+‎40m B.‎-40m C.+‎30m D.‎‎-30m ‎2.一个几何体的三视图如图所示，则这个几何体是（ D ）‎ ‎3.遵义市是国家级红色旅游市，每年都吸引众多海内外游客前来观光、旅游，据有关部门统计报道:2012年全市共接待游客3354万人次，将3354万用科学计数法表示为（ B ）‎ A、 B、 C、 D、‎ ‎4.如图，直线∥，若∠1=140°,∠2=70°，则∠3的度数是（ A ）‎ A、70° B、80° C、65° D、60°‎ ‎5.计算(-)的结果是（ D ）‎ A、 B、 C、 D、‎ ‎6.如图,在4×4正方形网格中，任取一个白色的小正方形并涂黑，使图中黑色部分的图形构成一个轴对称图形的概率是（ A ）‎ A、 B、 C、 D、‎ ‎7.),是正比例函数图象上的两点，下列判断中，正确的是（ D ）‎ A、 B、 C、当时 D、当时,‎ ‎8.如图，A、B两点在数轴上表示的数分别是a、b。则下列式子中成立的是( C )‎ A、a+b<0 B、-a<-b C、1-2a>1-2b D、|a|-|b|>0‎ ‎9.如图，将边长1cm的等边三角形ABC沿直线l向右翻动(不滑动)，点B从开始到结束，所经过的长度为( C )‎ A、 ‎ B、‎ C、 D、3cm 10. 二次函数y=ax+bx+c（x≠0）的图象如图所示，若M=a+b-c，N=4a-2b+c，P=2a-b，则M、N、P中，值小于0的数有( A )‎ A、3个 B、2个 C、1个 D、0个 ‎11.计算： .‎ ‎12.已知点P（3，-1）关于y轴的对称点Q的坐标是（a+b，1-b），则a的值为 25 .‎ ‎13.分解因式：x-x= x(x+1)(x-1) .‎ ‎14.如图，OC是⊙O的半径，AB是弦，且OC⊥AB，点P在⊙O上，∠APC=26°,则∠BOC= 52° .‎ ‎15.已知x=-2是方程x+mx-6=0的一个根，则方程的另一个根是 x=3 .‎ ‎16.如图，在矩形ABCD中，对角线AC，BD相交于点O，点E,F分别是AO,AD的中点，若AB=6cm，BC=8cm，则△AEF的周长= 9 .‎ ‎17.如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，E为BC边上的一点，以A为圆心，AE为半径的圆弧交于点D，交AC的延长线于点F，若图中两个阴影部分的面积相等，则AF的长为 .‎ C ‎18.如图，已知直线与双曲线（k＞0）交于点A,B两点，点B的坐标为（-4，-2）C为双曲线（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为 (2,4)或( 8,1) 。‎ ‎19.解方程组 解：由（1）得：x=4+2y (3)‎ 把（3）代入（2）得：2（4+2y)+y-3=0,解得y=,把y=代入（3）得x=‎ 所以是原方程组的解。‎ 20. 已知实数a满足，求的值.‎ 解 ‎=‎ ‎=‎ ‎=‎ ‎∵，∴，‎ 当a=3时，原式=;当a=-5时，原式=‎ ‎∴原式的值为。‎ ‎21.我市某中学在创建“特色校园”的活动中，将本校的办学理念做成宣传牌（AB），放置在教学楼的顶部（如图所示）。小明在操场上的点D处，用1m高的测角仪CD，从点C测得宣传牌的底部B的仰角为37º，然后向教学楼正方向走了4米到达点F处，又从点E测得宣传牌顶部A仰角为45º.已知教学楼高BM=17米，且点A、B、M在同一直线上，求宣传牌AB高度（结果精确到0.1米。参考数据：，sin37º≈0.60,cos37º≈0.81,tan37º≈0.75).‎ 解：延长CE到N与AM相交于N，在RtΔCNB中，tan∠BCN=,∵∠BCN=37º,BN=17-1=16,CE=4,∴tan37º=,解得EN=；在RtΔENA中，tan∠AEN=,∵∠AEN=45º,BN=16,EN=14,∴tan45º=,解得AB=≈1.3‎ 答：宣传牌AB高度约为1.3米.‎ 22. ‎“校园安全”受到全社会的广泛关注，某校政教处对部分学生及家长就校园安全知识的了解程度，进行了随机抽样调查，并绘制成如图所示的两幅统计图，请根据统计图中的信息，解答下列问题：‎ （1） 参与调查的学生及家长共有 400 人；‎ （2） 在扇形统计图中，“基本了解”所对应的圆心角的度数是 135 度；‎ （3） 在条形统计图中，“非常了解”所对应的学生人数是 62 人；‎ （4） 若全校有1200名学生，请估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人？885人 解：‎ ‎186+219=405（人）‎ 所以，“非常了解”和“基本了解”的学生人数共有405人。‎ 23. 一个不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出一个球是红球的概率为.‎ （1） 求口袋中黄球的个数.‎ （2） 甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用“树状图”或“列表法”，求两次摸出都是红球的概率.‎ （3） 现规定：摸到红球得5分，摸到黄球得3分，摸到蓝球得2分（每次摸后不放回），乙同学在一次摸球游戏中，第一次随机摸到一个红球，第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学第三次摸球所得分数之和不低于10分的概率.‎ 解：（1）设袋中有黄球x个，由题意得 ‎ ‎ ‎ 解得：‎ ‎ 经检验：是原方程的解，符合题意 ‎ 故袋中共有黄球1个.‎ ‎（2）画树状图如下：‎ 第一次 红1 红2 黄 蓝 第二次 红2 黄 蓝 红1 黄 蓝 红1 红2 蓝 红1 红2 蓝 ‎ 由树状图可知，共有12种等可能结果，其中两次都摸出红球有2种。‎ ‎ ‎ ‎ （3）第三次从袋子里摸球共有4种等可能结果，而满足3次摸得的总分不低于10分的结果有3种，所以，符合题意的概率是.‎ ‎24.如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N.‎ （1） 求证：CM=CN；‎ （2） 若ΔCMN的面积与ΔCDN的面积比为3：1，求的值 解：（1）证明：∵ 四边形AMNE是由四边形CMND折叠而得，且点C 与点A重合.‎ ‎ ∴ ‎ ‎ 四边形ABCD是矩形 ‎ ∴AD//BC.‎ ‎ ‎ ‎ ∴‎ ‎ ∴CM=CN.‎ (2) 过点N作NH┴BC,垂足为H,则四边形NHCD是矩形，∴HC=DN，NH＝DC。‎ ‎∵ΔＣＭＮ的面积与ΔCDN的面积比是３：１，∴‎ ‎∴MC＝３ND＝３HC，MH＝２HC。设DN＝x，则HC=x，MH=2x,∴CM=3x=CN;在RtΔCDN中，，∴HN=。同理：，∴。‎ ‎25.‎2013年4月20日，四川雅安发生7.0级地震，给雅安人民的生命财产带来巨大损失，某市民政部门将租用甲、乙两种货车共16辆，把粮食266吨、副食品169吨全部运到灾区。已知一辆甲种货车同时可装粮食18吨、副食品10吨；一辆乙种货车同时可装粮食16吨、副食品11吨.‎ （1） 若将这批货物一次性运到灾区，有哪几种租车方案？‎ （2） 若甲种货车每辆需付燃油费1500元；乙种货车每辆需付燃油费1200元，应选择（1）中的哪种租车方案，才能使所付的费用最少？最少费用是多少元？‎ 解：设租用甲种货车x辆，则甲种货车为（16-x）辆，由题意得：‎ ‎，解不等式组得5≤x≤7‎ ‎∵x为正整数，∴x=5或6或7‎ 因此，有3种租车方案，即：‎ 方案一：租甲种货车5辆，乙种货车11辆；‎ 方案二：租甲种货车6辆，乙种货车10辆；‎ 方案三：租甲种货车7辆，乙种货车9辆.‎ 26. 如图，在RtΔABC中，∠C=90º，AC=4cm,BC=3cm.动点M、N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A、B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t（单位：秒，00,∴S有最小值，当t=时，S最小值为 答：当t=时，四边形APNC的面积最小，S的最小值是.‎ ‎27.如图，已知抛物线 （a≠0）的顶点坐标为（4，），且与y轴交于点C（0，2），与x轴交于A、B两点（点A在点B的左边）.‎ （1） 求抛物线的解析式及A、B两点的坐标；‎ （1） 在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小，若存在，求AP+CP的最小值;若不存在，请说明理由；‎ （2） 在以AB为直径的⊙M中，CE与⊙M相切于点E，CE交x轴于点D，求直线CE的解析式.‎ 解：（1）由题意，设抛物线的解析式为（a≠0）.‎ ‎∵抛物线经过点C（0,2）‎ ‎∴解得a=‎ ‎∴，即当y=0时，解得 ∴A（2,0）B（6,0）‎ （2） 存在 ‎ 由（1）知，抛物线的对称轴l为x=4,因为A、B两点关于l 对称，连接CB交l于点P，则AP=BP，所以，AP+CP=BC的值最小，∵B（6,0），C（0,2），∴OB=6，OC=2 ∴BC== ∴AP+CP=BC= ∴AP+CP的最小值为.‎ (3) 连接ME ‎ ∵CE是⊙O的切线 ∴ME⊥CE,CEM=90º ∴COD=DEM=90º 由题意，得OC=ME=2，ODC=MDE ∴ΔCOD≌ΔMED ∴OD=DE,DC=DM 设OD=x，则CD=DM=OM-OD=4-x， 在RtΔCOD中， ∴ ∴x=,∴D(,0) 设直线CE的解析式为y=kx+b(k≠0),∵直线CE过C（0,2），D（，0）两点，则解得 ∴直线CE的解析式为y=.‎