山东省东营市2010年中考数学试题(含答案)

山东省东营市2010年中考数学试题(含答案)

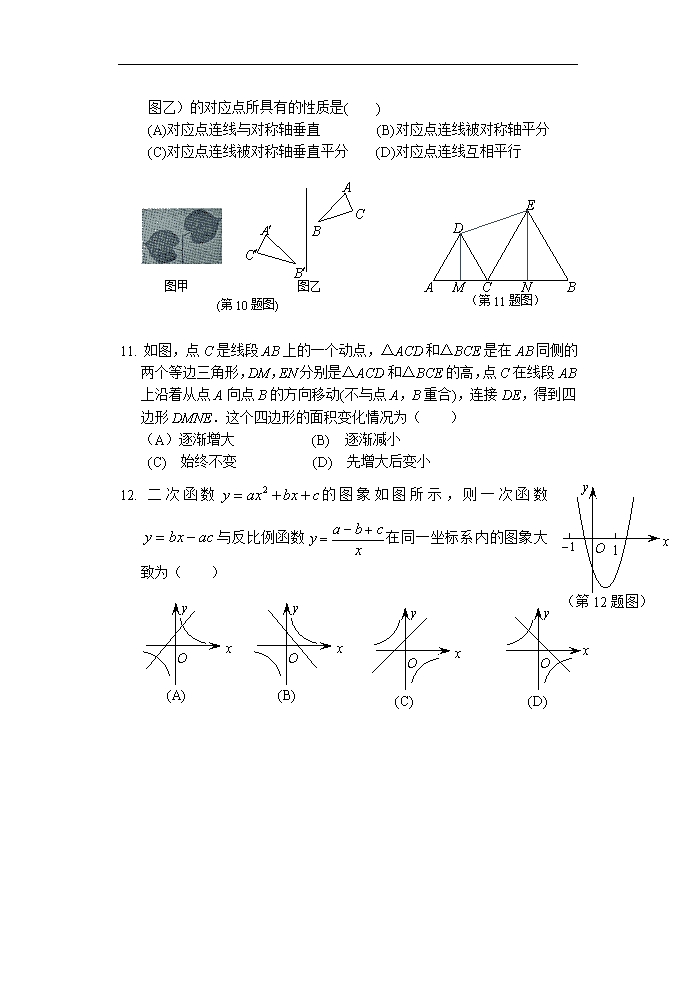
绝密★启用前 试卷类型:A 二○一○年东营市初中学生学业考试 数 学 试 题 ‎（总分120分 考试时间120分钟） ‎ 注意事项：‎ ‎1. 本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷3页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共11页．‎ ‎2. 答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．‎ ‎3. 第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．‎ ‎4. 考试时，不允许使用科学计算器．‎ 第Ⅰ卷（选择题 共36分） ‎ 一、选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分． ‎ ‎1．下列运算中，正确的是（ ）‎ ‎(A) (B) (C) (D)‎ ‎2. 64的立方根是( )‎ ‎ （A）4 （B）－4 （C）8 （D）－8‎ ‎3. 一次函数的图象不经过（ ）‎ ‎ (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限 ‎4．分式方程的解是（ ）‎ ‎，‎ ‎ (A)－3 (B) ‎2 ‎ (C)3 (D)－2‎ ‎5. 不等式组 的解集为( )‎ ‎(A)－1< x≤1 (B) －1≤x <1 (C) －1< x <1 (D) x <－1或x≥1‎ ‎6．如图，将三角尺的直角顶点放在直尺的一边上，，则的度数等于（ ）‎ ‎(A) (B) (C) (D)‎ ‎1‎ ‎2‎ ‎3‎ ‎（第6题图）‎ y ‎1‎ ‎2‎ ‎2‎ ‎1‎ A y2‎ y1‎ x ‎(第7题图)‎ O ‎ ‎ ‎7. 如图所示，反比例函数与正比例函数的图象的一个交点是，若，则的取值范围在数轴上表示为（ ）‎ ‎1‎ ‎2‎ ‎0‎ ‎（A）‎ ‎1‎ ‎2‎ ‎0‎ ‎(B)‎ ‎1‎ ‎2‎ ‎0‎ ‎(C)‎ ‎1‎ ‎2‎ ‎0‎ ‎(D)‎ A B C m ‎(第8题图)‎ ‎8. 如图，小明为了测量其所在位置A点到河对岸B点之间 的距离，沿着与AB垂直的方向走了m米，到达点C，‎ 测得∠ACB＝，那么AB等于（ ）‎ ‎(A) m·sin米 (B) m·tan米 ‎ ‎(C) m·cos米 (D) 米 ‎9. 有20张背面完全一样的卡片，其中8张正面印有天鹅湖风光，7张正面印有黄河入海口自然风景，5张正面印有孙武湖景色．把这些卡片的背面朝上，搅匀后从中随机抽出一张卡片，抽到正面是天鹅湖风光卡片的概率是（ ）‎ ‎(A) (B) (C) (D)‎ ‎10. 把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换（如图甲）．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换 过程中，两个对应三角形（如图乙）的对应点所具有的性质是( )‎ ‎(A)对应点连线与对称轴垂直 (B)对应点连线被对称轴平分 ‎(C)对应点连线被对称轴垂直平分 (D)对应点连线互相平行 A C B ‎(第10题图)‎ 图乙 图甲 A B C D E M N ‎（第11题图）‎ ‎11. 如图，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着从点A向点B的方向移动(不与点A，B重合)，连接DE，得到四边形DMNE．这个四边形的面积变化情况为（ ）‎ ‎（A）逐渐增大 (B) 逐渐减小 ‎ ‎ (C) 始终不变 (D) 先增大后变小 ‎1‎ O x y ‎（第12题图）‎ ‎12. 二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）‎ y x O ‎(B)‎ y x O ‎(A)‎ y x O ‎(C)‎ y x O ‎(D)‎ 绝密★启用前 试卷类型:A ‎ 二○一○年东营市初中学生学业考试 数 学 试 题 第Ⅱ卷（非选择题 共84分）‎ 注意事项：‎ ‎　1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．‎ ‎2．答卷前将密封线内的项目填写清楚．‎ 题号 二 三 总分 ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 得 分 评 卷 人 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13．上海世博会主题馆屋面太阳能板面积达3万多平方米，年发电量可达280万度.这里的280万度用科学记数法表示（保留三个有效数字）为_________________________度. ‎ ‎14．把分解因式，结果为________________________________.‎ ‎15．有一组数据如下: 3, a, 4, 6, 7. 它们的平均数是5，那么这组数据的方差为_________．‎ ‎16．将一直径为‎17cm的圆形纸片（图①）剪成如图②所示形状的纸片，再将纸片沿虚线折叠得到正方体（图③）形状的纸盒，则这样的纸盒体积最大为 cm3．‎ ‎（第16题图）‎ ‎①‎ ‎②‎ ‎③‎ ‎17. 观察下表，可以发现: 第_________个图形中的“△”的个数是“○”的个数的5倍.‎ 序号 ‎1‎ ‎2‎ ‎3‎ ‎…‎ 图形 ‎○‎ ‎○‎ ‎△‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎△‎ ‎△‎ ‎○‎ ‎△‎ ‎△‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎△‎ ‎△‎ ‎△‎ ‎○‎ ‎△‎ ‎△‎ ‎△‎ ‎○‎ ‎○‎ ‎△‎ ‎△‎ ‎△‎ ‎○‎ ‎○‎ ‎○‎ ‎○‎ ‎…‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ 得 分 评 卷 人 ‎18． (本题满分7分) 先化简，再求值：‎ ‎，其中 .‎ 座号 得 分 评 卷 人 ‎19． (本题满分9分) ‎ 如图，在平行四边形ABCD中，点E，F分别是AD，BC的中点.‎ A E D C F B ‎（第19题图）‎ 求证：（1）△ABE≌△CDF；‎ ‎　　 （2）四边形BFDE是平行四边形.‎ 得 分 评 卷 人 ‎20． (本题满分9分) ‎ 光明中学组织全校1 000名学生进行了校园安全知识竞赛．为了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的成绩（得分取正整数，满分为100分），并绘制了如图的频数分布表和频数分布直方图（不完整）．‎ 分组 频数 频率 ‎50.5~60.5‎ ‎10‎ a ‎60.5~70.5‎ b ‎70.5~80.5‎ ‎0.2‎ ‎80.5~90.5‎ ‎52‎ ‎0.26‎ ‎90.5~100.5‎ ‎0.37‎ 合计 c ‎1‎ 频数 ‎80‎ ‎70‎ ‎60‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎0‎ 成绩/分 ‎50.5 60.5 70.5 80.5 90.5 100.5‎ 请根据以上提供的信息，解答下列问题：‎ ‎（1）直接写出频数分布表中a，b ，c 的值，补全频数分布直方图；‎ ‎（2）上述学生成绩的中位数落在哪一组范围内？‎ ‎（3）学校将对成绩在90.5~100.5分之间的学生进行奖励，请估计全校1 000名学生中约有多少名获奖？‎ 得 分 评 卷 人 ‎21． (本题满分9分)‎ 如图，AB是⊙O的直径，点D在AB的延长线上，点C在⊙O上， CA＝CD，‎ ‎∠CDA＝30°．‎ ‎(1)试判断直线CD与⊙O的位置关系，并说明理由；‎ O ‎(第21题图)‎ A B D C ‎(2)若⊙O的半径为5，求点A到CD所在直线的距离．‎ 得 分 评 卷 人 ‎22． (本题满分10分)‎ 如图所示的矩形包书纸中，虚线是折痕，阴影是裁剪掉的部分，四个角均为大小相同的正方形，正方形的边长为折叠进去的宽度.‎ ‎（1）设课本的长为a cm，宽为b cm，厚为c cm，如果按如图所示的包书方式，将封面和封底各折进去‎3cm，用含a，b，c的代数式，分别表示满足要求的矩形包书纸的长与宽；‎ ‎（2）现有一本长为‎19cm，宽为‎16cm，厚为‎6cm的字典，你能用一张长为‎43cm，宽为‎26cm的矩形纸，按图所示的方法包好这本字典，并使折叠进去的宽度不小于‎3cm吗？请说明理由.‎ ‎（第22题图）‎ 封面 封底 得 分 评 卷 人 ‎23． (本题满分10分) ‎ 如图，已知二次函数的图象与坐标轴交于点A（-1， 0）和点 B（0，-5）．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）已知该函数图象的对称轴上存在一点P，使得△ABP的周长最小．请求出点P的坐标．‎ x O A ‎（第23题图）‎ B y 得 分 评 卷 人 ‎24． (本题满分10分) ‎ 如图，在锐角三角形ABC中，，△ABC的面积为48，D，E分别是边AB，AC上的两个动点（D不与，重合），且保持DE∥BC，以DE为边，在点的异侧作正方形DEFG.‎ ‎（1）当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；‎ B ‎（第24题图）‎ A D E F G C B ‎（备用图（1））‎ A C B ‎（备用图（2））‎ A C ‎（2）设DE = x，△ABC与正方形DEFG重叠部分的面积为，试求关于的函数关系式，写出x的取值范围，并求出y的最大值.‎ 绝密★启用前 试卷类型:A ‎2010年东营市初中学生学业考试 数学试题参考答案与评分标准 评卷说明：‎ ‎1. 选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2. 解答题中的每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．本答案对每小题只给出一种解法，对考生的其他解法，请参照评分意见进行评分．‎ ‎3. 如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一.选择题：本大题共12小题,共３６分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分． ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C A B C A C D B C B C B 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13． 2.80×106； 14．； 15． 2； 　16．； 17. 20.‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ ‎18． (本题满分7分) ‎ 解：‎ ‎ …………………………………3分 ‎. 5分 把代入上式，得 原式=.………………7分 ‎19． (本题满分9分) ‎ A E D C F B ‎（第19题图）‎ 证明:（1）在平行四边形ABCD中，AB=CD，AD=CB.‎ ‎ 又点E，F分别是AD，BC的中点. ………1分 ‎ AE=CF, …………………………3分 ‎ ,…………………4分 ‎ △ABE≌△DCF (边，角，边) ……5分 ‎（2）在平行四边形BFDE中，‎ ‎∵△ABE≌△DCF ,‎ ‎ BE=DF. ………………………………………6分 ‎ 又点E，F分别是AD，BC的中点.‎ DE=BF, ……………………………………………8分 四边形BFDE是平行四边形. …………………9分 ‎20． (本题满分9分) ‎ 解：（1）…………………………………3分 作图略. …………………………………………………………4分 ‎（2）80.5~90.5； …………………………………………………6分 ‎（3）370人． …………………………………………………9分 O ‎(第21题图)‎ A B D C E ‎21． (本题满分9分)‎ 解：（1）△ACD是等腰三角形，∠D＝30°．‎ ‎ ∠CAD=∠CDA=30°. ‎ 连接OC, AO=CO,‎ ‎ △AOC是等腰三角形． ………………………2分 ‎ ∠CAO=∠ACO=30°,‎ ‎ ∠COD=60°．…………………………………3分 ‎ 在△COD中，又∠CDO=30°，‎ ‎∠DCO=90°．………………………………4分 CD是⊙O的切线，即直线CD与⊙O相切．……………5分 ‎（2）过点A 作AE⊥CD，垂足为E. ………………………6分 在Rt△COD中， ‎ ‎∠CDO=30°，‎ ‎ OD=2OC=10． AD=AO+OD=15…………………7分 ‎ 在Rt△ADE中，‎ ‎ ∠EDA=30°，‎ 点A到CD边的距离为：．…9分 ‎22． (本题满分10分) ‎ 解：（1）矩形包书纸的长为：（2b+c+6）cm，…………………………………………2分 矩形包书纸的宽为（a+6）cm. ……………………4分 ‎(2)设折叠进去的宽度为xcm，……………………………5分 ‎（第22题图）‎ 封面 封底 分两种情况：‎ ‎≤‎ ‎≤‎ ‎①当字典的长与矩形纸的宽方向一致时，根据题意，得………………………………7分 解得x≤2.5. ‎ 所以不能包好这本字典. …………………8分 ‎②当字典的长与矩形纸的长方向一致时，同理可得 x≤-6. 所以不能包好这本字典. ……………………9分 综上，所给矩形纸不能包好这本字典. …………10分 x O A ‎（第23题图）‎ B y C P x=2‎ ‎23． (本题满分10分)‎ 解：（1）根据题意，得…2分 解得 ……………………3分 ‎∴二次函数的表达式为．……4分 ‎（2）令y=0，得二次函数的图象与x轴 的另一个交点坐标C（5, 0）.……………5分 由于P是对称轴上一点，‎ 连结AB，由于，‎ 要使△ABP的周长最小，只要最小.……………6分 由于点A与点C关于对称轴对称，连结BC交对称轴于点P，则= BP+PC =BC，根据两点之间，线段最短，可得的最小值为BC.‎ 因而BC与对称轴的交点P就是所求的点.………………8分 设直线BC的解析式为，根据题意，可得解得 所以直线BC的解析式为.……………………9分 B ‎（第24题图(1)）‎ A D E F G C M N 因此直线BC与对称轴的交点坐标是方程组的解，解得 所求的点P的坐标为（2，-3）.…………………10分 ‎24． (本题满分10分) ‎ 解：（1）当正方形DEFG的边GF在BC上时，如图 ‎（1），过点A作BC边上的高AM，交DE于N，垂足为M.‎ ‎∵S△ABC=48，BC=12，∴AM=8.‎ ‎∵DE∥BC，△ADE∽△ABC, ………1分 ‎∴，‎ 而AN=AM－MN=AM－DE，∴. ………2分 解之得.‎ ‎∴当正方形DEFG的边GF在BC上时，正方形DEFG的边长为4.8.…3分 B ‎（第24题图（2））‎ A D E F G C ‎（2）分两种情况：‎ ‎①当正方形DEFG在△ABC的内部时，如图（2），△ABC 与正方形DEFG重叠部分的面积为正方形DEFG的面积，‎ ‎∵DE=x，∴，此时x的范围是≤4.8…4分 ‎②当正方形DEFG的一部分在△ABC的外部时，‎ 如图（2），设DG与BC交于点Q，EF与BC交于点P，‎ ‎△ABC的高AM交DE于N，‎ ‎∵DE=x，DE∥BC，∴△ADE∽△ABC, …………5分 M B ‎（第24题图(3)）‎ A D E F G C N P Q 即，而AN=AM－MN=AM－EP, ‎ ‎∴，解得.………6分 所以, 即.………7分 由题意，x>4.8，x<12,所以.‎ 因此△ABC与正方形DEFG重叠部分的面积为 ‎(0< x≤4.8)‎ ‎ ……………………8分 当≤4.8时，△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04‎ 当时，因为，所以当时，‎ ‎△ABC与正方形DEFG重叠部分的面积的最大值为.‎ 因为24>23.04，‎ 所以△ABC与正方形DEFG重叠部分的面积的最大值为24. …10分