中考数学概率统计大题专题复习

中考数学概率统计大题专题复习

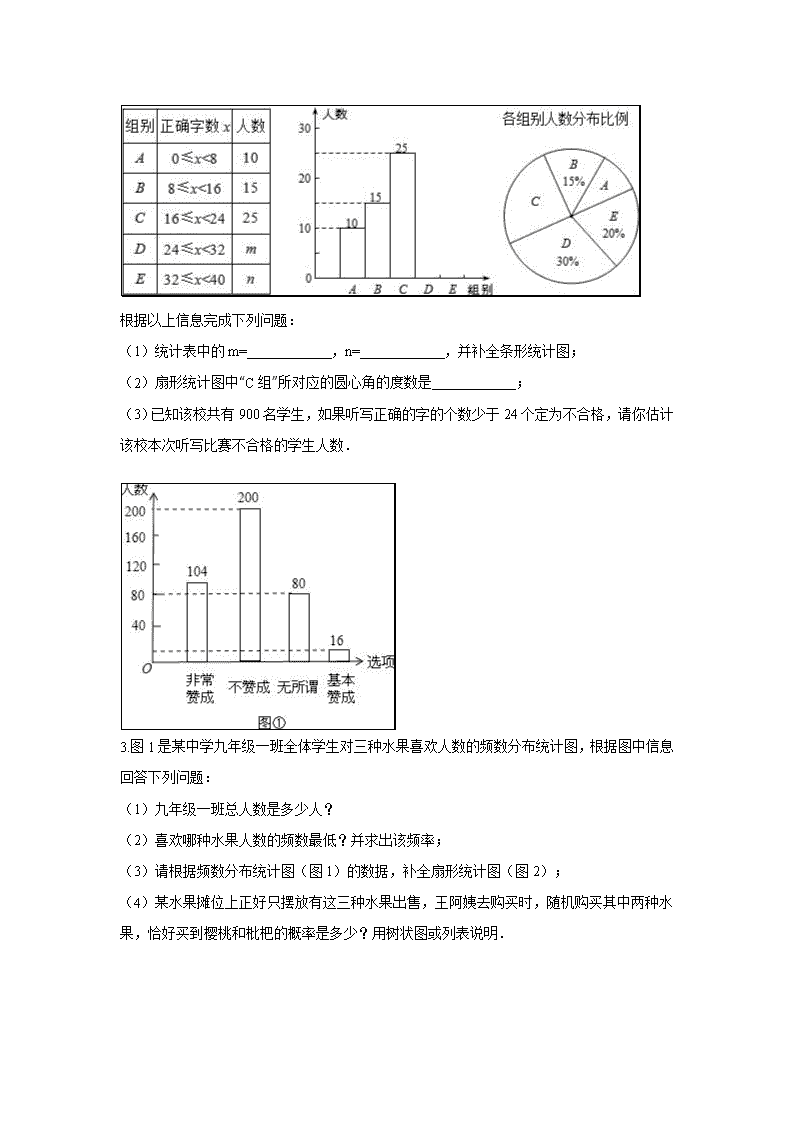
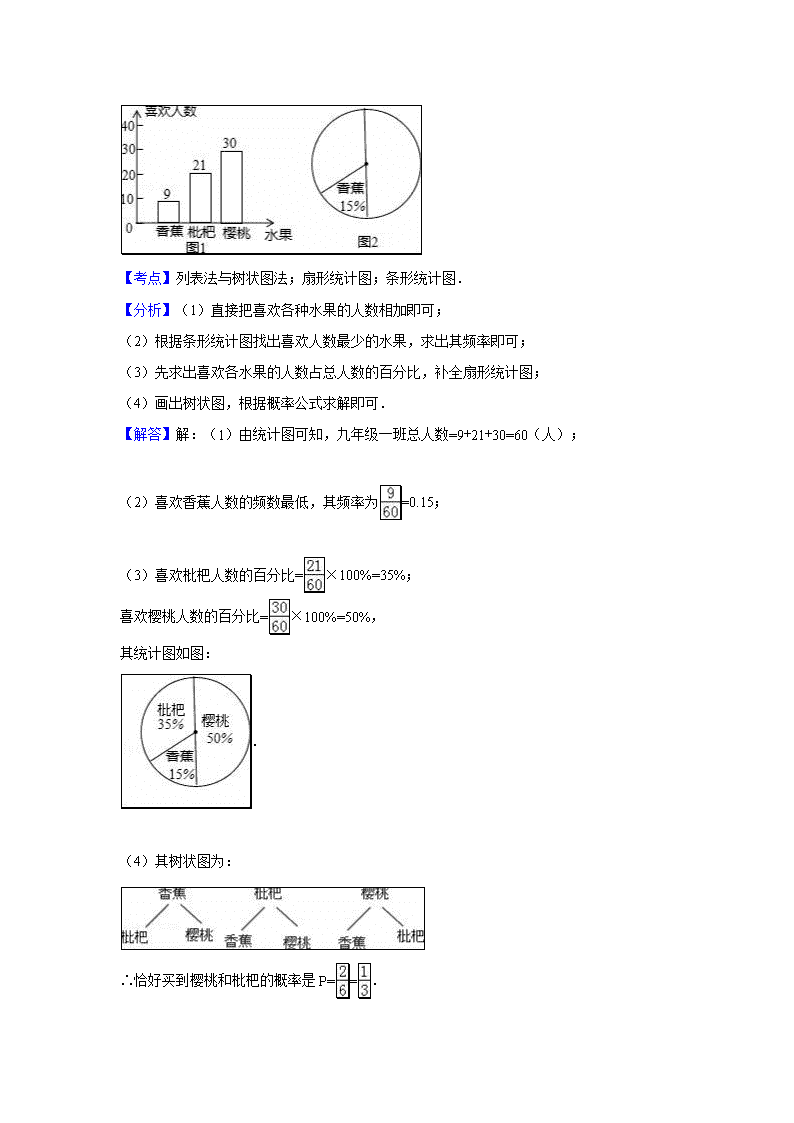
中考数学概率统计大题专题复习 ‎1.“校园手机”现象越来越受到社会的关注．小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法，统计整理并制作了如下的统计图：‎ ‎（1）求这次调查的家长总数及家长表示“无所谓”的人数，并补全图①；‎ ‎（2）求图②中表示家长“无所谓”的圆心角的度数；‎ ‎（3）若该学校有2000名家长，请根据该统计结果估算表示“基本赞成”的家长有多少人？‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）根据不赞成的有200人，占50%，可求出总人数，求出无所谓所占的百分比就可求出总人数×无所谓所占的百分比，然后补全图就可以．‎ ‎（2）360°×无所谓所占的百分比就是圆心角的度数．‎ ‎（3）2000乘以基本赞成所占的百分比就是所求．‎ ‎【解答】解：（1）家长总数：200÷50%=400人 家长表示“无所谓”的人数：400﹣200﹣16﹣400×26%=80人．‎ ‎（2）表示家长“无所谓”的圆心角的度数：；‎ ‎（3）恰好是“基本赞成”态度的家长的概率是：，‎ 人数大约有：2000×4%=80人．‎ ‎2.某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．‎ 根据以上信息完成下列问题：‎ ‎（1）统计表中的m=　　　　　　，n=　　　　　　，并补全条形统计图；‎ ‎（2）扇形统计图中“C组”所对应的圆心角的度数是　　　　　　；‎ ‎（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．‎ ‎3.图1是某中学九年级一班全体学生对三种水果喜欢人数的频数分布统计图，根据图中信息回答下列问题：‎ ‎（1）九年级一班总人数是多少人？‎ ‎（2）喜欢哪种水果人数的频数最低？并求出该频率；‎ ‎（3）请根据频数分布统计图（图1）的数据，补全扇形统计图（图2）；‎ ‎（4）某水果摊位上正好只摆放有这三种水果出售，王阿姨去购买时，随机购买其中两种水果，恰好买到樱桃和枇杷的概率是多少？用树状图或列表说明．‎ ‎【考点】列表法与树状图法；扇形统计图；条形统计图．‎ ‎【分析】（1）直接把喜欢各种水果的人数相加即可；‎ ‎（2）根据条形统计图找出喜欢人数最少的水果，求出其频率即可；‎ ‎（3）先求出喜欢各水果的人数占总人数的百分比，补全扇形统计图；‎ ‎（4）画出树状图，根据概率公式求解即可．‎ ‎【解答】解：（1）由统计图可知，九年级一班总人数=9+21+30=60（人）；‎ ‎（2）喜欢香蕉人数的频数最低，其频率为=0.15；‎ ‎（3）喜欢枇杷人数的百分比=×100%=35%；‎ 喜欢樱桃人数的百分比=×100%=50%，‎ 其统计图如图：‎ ‎．‎ ‎（4）其树状图为：‎ ‎∴恰好买到樱桃和枇杷的概率是P==．‎ ‎【点评】本题考查的是列表法与树状法，熟知条形统计图与扇形统计图的意义是解答此题的关键．‎ ‎4.某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动，现从中随机抽取部分作品，按A，B，C，D四个等级进行评价，并根据结果绘制了如下两幅不完整的统计图．‎ ‎（1）求抽取了多少份作品；‎ ‎（2）此次抽取的作品中等级为B的作品有　48　，并补全条形统计图；‎ ‎（3）若该校共征集到800份作品，请估计等级为A的作品约有多少份．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【专题】计算题．‎ ‎【分析】（1）根据C的人数除以占的百分比，得到抽取作品的总份数；‎ ‎（2）由总份数减去其他份数，求出B的份数，补全条形统计图即可；‎ ‎（3）求出A占的百分比，乘以800即可得到结果．‎ ‎【解答】解：（1）根据题意得：30÷25%=120（份），‎ 则抽取了120份作品；‎ ‎5.每年5月的第二周为我国城市节约用水宣传周。某社区为了做好今年居民节约用水的宣传，从本社区6000户家庭中随机抽取200户，调查他们家庭今年三月份的用水量，并将调查的结果绘制成如下的两幅不完整的统计图表：‎ 请根据上面的统计图表，解答下列问题：‎ ‎（1）在频数分布表中：m=________，n=________；‎ ‎（2）根据题中数据补全频数直方图；‎ ‎（3）如果自来水公司将基本月用水量定为每户12吨，不超过基本月用水量的部分享受基本价格，超出基本月用水量的部分实行加价收费。请估计该社区约有多少户家庭三月份的用水量超过基本月用水量？‎ 解：（1）40 0.25 ……………………2分（每空1分）‎ ‎ （2）补全频数直方图如图……………………4分 ‎（3）6 000×（0.25+0.09）=2040 ……………………7分 答：该社区约有2040户家庭三月份的用水量超过基本月用水量. …………8分 ‎6.垃圾的分类处理与回收利用，可以减少污染，节省资源，生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理，某城市环保部门为了提高宣传实效，抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况，并将调查统计结果绘制成如下两幅不完整的统计图表：‎ 根据图表解答下列问题：‎ ‎（1）请将条形统计图补充完整；‎ ‎（2）在抽样数据中，产生的有害垃圾共　3　吨；‎ ‎（3）调查发现，在可回收物中塑料类垃圾占，每回收1吨塑料类垃圾可获得0.7吨二级原料．假设该城市每月产生的生活垃圾为5000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？‎ ‎【考点】条形统计图；统计表；扇形统计图．‎ ‎【分析】（1）根据D类垃圾量和所占的百分比即可求得垃圾总数，然后乘以其所占的百分比即可求得每个小组的频数从而补全统计图；‎ ‎（2）求得C组所占的百分比，即可求得C组的垃圾总量；‎ ‎（3）首先求得可回收垃圾量，然后求得塑料颗粒料即可．‎ ‎【解答】解：（1）观察统计图知：D类垃圾有5吨，占10%，‎ 垃圾总量为5÷10%=50（吨），‎ 故B类垃圾共有50×30%=15（吨），‎ 如图所示：‎ ‎（2）∵C组所占的百分比为：1﹣10%﹣30%﹣54%=6%，‎ ‎∴有害垃圾为：50×6%=3（吨），‎ 故答案为：3；‎ ‎（3）5000×54%××0.7=378（吨），‎ 答：每月回收的塑料类垃圾可以获得378吨二级原料．‎ ‎【点评】本题考查条形统计图、用样本估计总体、扇形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键，条形统计图能清楚地表示出每个项目的数据．‎ ‎7.小明对所在班级的“小书库”进行了分类统计，并制作了如下的统计图表：根据上述信息，完成下列问题：‎ ‎（1）图书总册数是　100　册，a=　14　册；‎ ‎（2）请将条形统计图补充完整； ‎ 类别 语文 数学 英语 物理 化学 其他 数量（册）‎ ‎22‎ ‎20‎ ‎18‎ a ‎12‎ ‎14‎ 频率 ‎0.14‎ ‎（3）数据22，20，18，a，12，14中的众数是　14　，极差是　10　；‎ ‎（4）小明从这些书中任意拿一册来阅读，求他恰好拿到数学或英语书的概率．‎ ‎【考点】条形统计图；众数；极差；概率公式．‎ ‎【专题】数形结合．‎ ‎【分析】（1）用其他类的册数除以频率即可求出总本数，再减去已知的本书即可求出a的值．‎ ‎（2）根据上题求出的结果将统计图补充完整即可．‎ ‎（3）根据众数与极差的概念直接解答即可．‎ ‎（4）根据概率的求法，用数学与英语书的总本数除以总本数即可解答．‎ ‎【解答】解：（1）总本数=14÷0.14=100本，a=100﹣22﹣20﹣18=12﹣14=14本．‎ ‎（2）如图：‎ ‎（3）数据22，20，18，a，12，14中a=14，所以众数是 14，极差是22﹣12=10；‎ ‎（4）（20+18）÷100=0.38，即恰好拿到数学或英语书的概率为0.38．‎ 故答案为100，14，14，10．‎ ‎【点评】本题考查的是条形统计图和统计表的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．‎ ‎8.八年级（1）班学生在完成课题学习“体质健康测试中的数据分析”后，利用课外活动时间积极参加体育锻炼，每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练，训练后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图．‎ 请你根据上面提供的信息回答下列问题：‎ ‎（1）扇形图中跳绳部分的扇形圆心角为　36　度，该班共有学生　40　人，训练后篮球定时定点投篮平均每个人的进球数是　5　．‎ ‎（2）老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试，请用列表或画树形图的方法求恰好选中两名男生的概率．‎ ‎【考点】列表法与树状图法；扇形统计图；条形统计图．‎ ‎【分析】（1）跳绳部分的圆心角的度数用周角乘以跳绳部分所占的百分比即可；总人数用用篮球的总人数除以其所占的百分比即可求得总人数；‎ ‎（2）列树状图将所有等可能的结果列举出来后利用概率公式求解即可．‎ ‎【解答】解：（1）扇形图中跳绳部分的扇形圆心角为360°×（1﹣50%﹣20%﹣10%﹣10%）=36度；‎ 该班共有学生（2+5+7+4+1+1）÷50%=40人；‎ 训练后篮球定时定点投篮平均每个人的进球数是=5，‎ 故答案为：36，40，5．‎ ‎（2）三名男生分别用A1，A2，A3表示，一名女生用B表示．根据题意，可画树形图如下：‎ 由上图可知，共有12种等可能的结果，选中两名学生恰好是两名男生（记为事件M）的结果有6种，‎ ‎∴P（M）==．‎ ‎【点评】此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验；注意概率=所求情况数与总情况数之比 ‎9.某学习小组由3名男生和1名女生组成，在一次合作学习后，开始进行成果展示．‎ ‎（1）如果随机抽取1名同学单独展示，那么女生展示的概率为　　；‎ ‎（2）如果随机抽取2名同学共同展示，求同为男生的概率．‎ ‎【考点】列表法与树状图法．‎ ‎【分析】（1）4名学生中女生1名，求出所求概率即可；‎ ‎（2）列表得出所有等可能的情况数，找出同为男生的情况数，即可求出所求概率．‎ ‎【解答】解：（1）如果随机抽取1名同学单独展示，那么女生展示的概率为；‎ ‎（2）列表如下：‎ 男 男 男 女 男 ‎﹣﹣﹣‎ ‎（男，男）‎ ‎（男，男）‎ ‎（女，男）‎ 男 ‎（男，男）‎ ‎﹣﹣﹣‎ ‎（男，男）‎ ‎（女，男）‎ 男 ‎（男，男）‎ ‎（男，男）‎ ‎﹣﹣﹣‎ ‎（女，男）‎ 女 ‎（男，女）‎ ‎（男，女）‎ ‎（男，女）‎ ‎﹣﹣﹣‎ 所有等可能的情况有12种，其中同为男生的情况有6种，‎ 则P==．‎ ‎【点评】此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．‎ ‎10.九年级某班组织班团活动，班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品，已知钢笔2元／支，笔记本1元／本，且每样东西至少买一件.‎ ‎⑴ 有多少种购买方案？请列举所有可能的结果；‎ ‎⑵ 从上述方案中任选一种方案购买，求买到的钢笔与笔记本数量相等的概率.‎ ‎【答案】解：（1）设买钢笔x支，笔记本y本，则2x+y=15，所以y=15-2x。当x=1时，y=13；x=2时，y=11；x=3时，y=9；x=4时，y=7；x=5时，y=5；x=6时，y=3；x=7时，y=1；所以共有7种购买方案.‎ ‎（2）在这7种方案中，买到的钢笔与笔记本数量相等的只有一种，所以P（买到的钢笔与笔记本数量相等）=．‎ ‎11.有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字－l，－2和－3．小强从A布袋中随机取出一个小球，记录其标有的数字为a，再从B布袋中随机取出一个小球，记录其标有的数字为b，这样就确定点Q的一个坐标为（a，b）．‎ ‎ ⑴用列表或画树状图的方法写出点Q的所有可能坐标；‎ ‎ ⑵求点Q落在直线y=x－3上的概率．‎ ‎【答案】（1）列表或画树状图略，点Q的坐标有 ‎（1，-1），（1，-2），（1，-3），（2，-1），（2，-2），（2，-3）；‎ ‎（2）“点Q落在直线y = x-3上”记为事件，所以，‎ 即点Q落在直线y = x-3上的概率为．‎ ‎12.某中学开展“校园文化节“活动，对学生参加书法比赛的作品按A、B、C、D四个等级进行了评定．现随机抽取部分参赛学生书法作品的评定结果进行统计分析，并将分析结果绘制成如图扇形统计图（图①）和条形统计图（图②），根据所给信息完成下列问题：‎ ‎（1）本次抽取的样本的容量为　120　；‎ ‎（2）在图①中，C级所对应的扇形圆心角度数是　108°　；‎ ‎（3）请在图②中将条形统计图补充完整；‎ ‎（4）已知该校本次活动学生参赛的书法作品共750件，请你估算参赛作品中A级和B级作品共多少件？‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）根据A级人数为24人，以及在扇形图中所占比例为20%，24÷20%即可得出抽取的样本的容量；‎ ‎（2）用360°乘以C级所占的百分比即可得出答案；‎ ‎（3）根据C级在扇形图中所占比例为30%，得出C级人数为：120×30%=36人，即可得出B级人数，补全条形图即可；‎ ‎（4）先求出A级和B级作品在样本中所占的百分比，再乘以总的作品，即可得出答案．‎ ‎【解答】解：（1）∵A级人数为24人，在扇形图中所占比例为20%，‎ ‎∴这次抽取的样本的容量为：24÷20%=120；‎ 故答案为：120；‎ ‎（2）C级所对应的扇形圆心角度数是360°×30%=108°；‎ 故答案为：108°；‎ ‎（3）根据C级在扇形图中所占比例为30%，‎ 得出C级人数为：120×30%=36（人），‎ 则B级人数为：120﹣36﹣24﹣12=48（人），‎ 如图所示：‎ ‎（4）∵A级和B级作品在样本中所占比例为：（24+48）÷120×100%=60%，‎ ‎∴该校这次活动共收到参赛作品750份，参赛作品达到B级以上有750×60%=450份．‎ ‎【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎13.两会期间，“全民阅读”被再次写进《政府工作报告》，成为社会热词．在第20个世界读书日来临之际，我市某中学为了解本校学生每周课外阅读时间t（单位：小时），采用随机抽样的方法进行问卷调查，调查结果按0≤t＜0.5，0.5≤t＜1，1≤t＜2，2≤t分为四个等级，分别用A、B、C、D表示，并绘制成了两幅不完整的统计图，由图中给出的信息回答下列问题：‎ ‎（1）填空：A等级的百分率是　5　%；B等级的百分率是　15　%；‎ ‎（2）将不完整的条形统计图补充完整；‎ ‎（3）若该校共有学生2400人，试估计每周课外阅读时间量满足t≥1的人数．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）先求出总人数，再求出样本中C等级人数及A等级人数，即可求出A等级的百分率及B等级的百分率，‎ ‎（2）求出C等级人数及A等级人数，补全统计图即可，‎ ‎（3）求出样本中满足t≥1的人数，再求出样本中满足t≥1的百分比，用总人数乘这个百分比即可．‎ ‎【解答】解：（1）样本的总人数：（人），‎ 样本中C等级：200×45%=90（人），‎ 样本中A等级：200﹣30﹣90﹣70=10（人）‎ A等级的百分率是=5%；B等级的百分率是=15%；‎ 故答案为：5，15．‎ ‎（2）样本中A等级：200×5%=10（人），‎ 样本中C等级：200×45%=90（人），‎ ‎（3）样本中满足t≥1的人数：90+70=160（人）‎ 样本中满足t≥1的百分比为： =80%，‎ 该校共有学生2400人，时间量满足t≥1的人数：2400×80%=1920（人）．‎ 答：该校共有学生2400人，时间量满足t≥1的人数是1920人．‎ ‎【点评】本题主要考查了条形统计图，扇形统计图及用样本估计总体，解题的关键是读懂统计图，从统计图中获得准确的信息．‎ ‎　‎ ‎14.某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示．‎ 请根据统计图回答下列问题：‎ ‎（1）将条形统计图和扇形统计图在图中补充完整；‎ ‎（2）若A馆门票仅剩下一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽．若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华．”请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平？‎ ‎【考点】游戏公平性；扇形统计图；条形统计图；列表法与树状图法．‎ ‎【专题】图表型．‎ ‎【分析】（1）A展馆的门票数除以它所占的百分比，算出门票总数，乘以B展馆门票所占的百分比即为B展馆门票数；C所占的百分比等于整体1减去其余百分比；‎ ‎（2）列举出所有情况，看小明抽得的数字比小华抽得的数字大的情况占所有情况的多少即可求得小明赢的概率，进而求得小明赢的概率，比较即可．‎ ‎【解答】解：（1）‎ B展馆门票的数量=20÷10%×25%=50（张）；C所占的百分比=1﹣10%﹣25%﹣10%﹣40%=15%．‎ ‎（2）画树状图 或列表格法． ‎ ‎ 小华抽到的数字 小明抽到的数字 ‎1 ‎ ‎2 ‎ ‎3 ‎ ‎4 ‎ ‎ 1‎ ‎（1，1）‎ ‎（1，2）‎ ‎ （1，3）‎ ‎ （1，4）‎ ‎ 2‎ ‎ （2，1）‎ ‎ （2，2）‎ ‎ （2，3）‎ ‎ （2，4）‎ ‎ 3‎ ‎ （3，1）‎ ‎ （3，2）‎ ‎ （3，3）‎ ‎ （3，4）‎ ‎ 4‎ ‎ （4，1）‎ ‎ （4，2）‎ ‎ （4，3）‎ ‎ （4，4）‎ 共有16种可能的结果，且每种结果的可能性相同，其中小明可能获得门票的结果有6种，分别是（2，1），（3，1），（3，2），（4，1），（4，2），（4，3）．‎ ‎∴小明获得门票的概率，‎ 小华获得门票的概率．‎ ‎∵P1＜P2，‎ ‎∴这个规则对双方不公平．‎ ‎【点评】如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=，注意本题是放回实验．解决本题的关键是得到相应的概率，概率相等就公平，否则就不公平．‎ ‎15.阅读对人成长的影响是很大的、希望中学共有1500名学生，为了了解学生课外阅读的情况，就“你最喜欢的图书类别”（只选一项）随机调查了部分学生，并将调查结果统计后绘制成如下统计表和条形统计图．请你根据统计图表提供的信息解答下列问题：‎ 种类 频数 频率 科普 ‎0.15‎ 艺术 ‎78‎ 文学 ‎0.59‎ 其它 ‎81‎ ‎（1）这次随机调查了　300　名学生；‎ ‎（2）把统计表和条形统计图补充完整；‎ ‎（3）随机调查一名学生，恰好是最喜欢文学类图书的概率是多少？‎ ‎【考点】条形统计图；频数（率）分布表；概率公式．‎ ‎【专题】阅读型．‎ ‎【分析】（1）根据统计表中，科普的人数是45人，占0.15；根据频数与频率的关系，可知共随机调查了45÷0.15=300（人）；‎ ‎（2）根据统计表中的数据：易知其它数值，据此可补全条形图；‎ ‎（3）由条形图可知：喜欢文学类图书有96人，占总人数的32%；故随机调查一名学生，估计恰好是最喜欢文学类图书的概率是32%．‎ ‎【解答】解：（1）这次随机调查的人数：45÷0.15=300（人）；‎ 故答案为：300；‎ ‎（2）根据统计表中的数据：‎ 艺术的有78人，占1﹣0.15﹣0.59=0.26，即频率为26%；‎ 文学的有300﹣78﹣45﹣81=96（人），‎ 据此可补全条形图：‎ 种类 频数 频率 科普 ‎45‎ ‎0.15‎ 艺术 ‎78‎ ‎0.26‎ 文学 ‎96‎ ‎0.59‎ 其它 ‎81‎ ‎（3）随机调查一名学生，估计恰好是最喜欢文学类图书的概率是96÷300×100%=32%．‎ ‎【点评】本题考查的是条形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．用到的知识点为：总体数目=部分数目÷相应百分比．概率=所求情况数与总情况数之比．‎