2017年度高考数学快速命中考点18
2014高考数学快速命中考点18
1.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,则C的方程是( )
A.-=1 B.-=1
C.-=1 D.-=1
【解析】 右焦点为F(3,0)说明两层含义:双曲线的焦点在x轴上;c=3.又离心率为=,故a=2,b2=c2-a2=32-22=5,故C的方程为-=1,选B.
【答案】 B
2.设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( )
A. B.
C. D.
【解析】 因为PF2⊥F1F2,∠PF1F2=30°,
所以|PF2|=2ctan 30°=c,|PF1|=c.
又|PF1|+|PF2|=c=2a,则e===.
【答案】 D
3.抛物线y2=4x的焦点到双曲线x2-=1的渐近线的距离是( )
A. B. C.1 D.
【解析】 由题意可得抛物线的焦点坐标为(1,0),
双曲线的渐近线方程为x±y=0,
则焦点到渐近线的距离d==.
【答案】 B
4.设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
A.(0,2) B.[0,2]
C.(2,+∞) D.[2,+∞)
【解析】 ∵x2=8y,∴焦点F的坐标为(0,2),准线方程为y=-2.由抛物线的定义知|MF|=y0+2.以F为圆心、|FM|为半径的圆的标准方程为x2+(y-2)2=(y0+2)2.
由于以F为圆心、|FM|为半径的圆与准线相交,又圆心F到准线的距离为4,故4
2.
【答案】 C
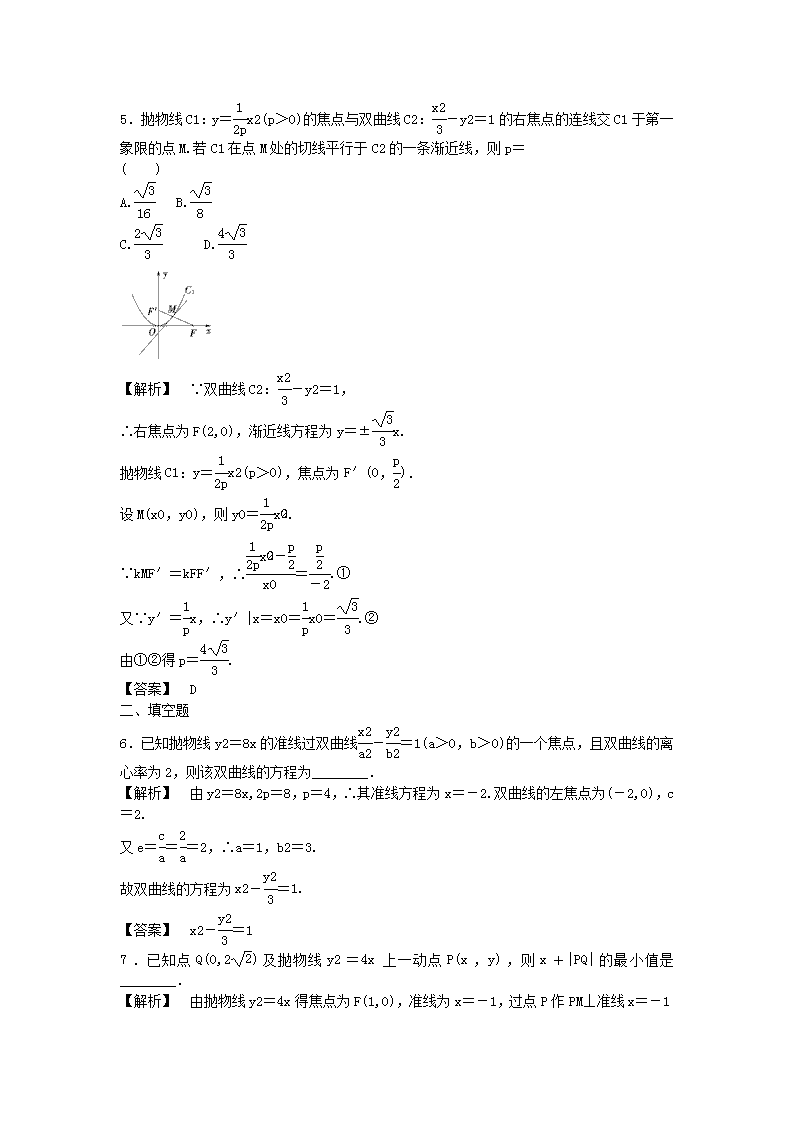
5.抛物线C1:y=x2(p>0)的焦点与双曲线C2:-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=
( )
A. B.
C. D.
【解析】 ∵双曲线C2:-y2=1,
∴右焦点为F(2,0),渐近线方程为y=±x.
抛物线C1:y=x2(p>0),焦点为F′(0,).
设M(x0,y0),则y0=x.
∵kMF′=kFF′,∴=.①
又∵y′=x,∴y′|x=x0=x0=.②
由①②得p=.
【答案】 D
二、填空题
6.已知抛物线y2=8x的准线过双曲线-=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.
【解析】 由y2=8x,2p=8,p=4,∴其准线方程为x=-2.双曲线的左焦点为(-2,0),c=2.
又e===2,∴a=1,b2=3.
故双曲线的方程为x2-=1.
【答案】 x2-=1
7.已知点Q(0,2)及抛物线y2=4x上一动点P(x,y),则x+|PQ|的最小值是________.
【解析】 由抛物线y2=4x得焦点为F(1,0),准线为x=-1,过点P作PM⊥
准线x=-1于点M,
则|PM|=|PF|=x+1.
∴x+|PQ|=|PM|+|PQ|-1=|PF|+|PQ|-1.
∵当F,P,Q三点共线时,|PF|+|PQ|最小,(|PF|+|PQ|)min=|FQ|==3,
∴(x+|PQ|)min=(|PF|+|PQ|-1)min=3-1=2.
【答案】 2
8.椭圆Γ:+=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=(x+c)与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
【解析】 已知F1(-c,0),F2(c,0),
直线y=(x+c)过点F1,且斜率为,
∴倾斜角∠MF1F2=60°.
∵∠MF2F1=∠MF1F2=30°,
∴∠F1MF2=90°,∴|MF1|=c,|MF2|=c.
由椭圆定义知|MF1|+|MF2|=c+c=2a,
∴离心率e===-1.
【答案】 -1
三、解答题
9.已知椭圆C1:+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,=2,求直线AB的方程.
【解】 (1)由已知可设椭圆C2的方程为+=1(a>2),其离心率为,故=,解得a=4.
故椭圆C2的方程为+=1.
(2)A,B两点的坐标分别记为(xA,yA),(xB,yB),
由=2及(1)知,O,A,B三点共线且点A,B不在y轴上,因此可设直线AB的方程为y=kx.
将y=kx代入+y2=1中,得(1+4k2)x2=4,
所以x=.
将y=kx代入+=1中,得(4+k2)x2=16,
所以x=.
又由=2,得x=4x,即=,
解得k=±1.故直线AB的方程为y=x或y=-x.
10.如图5-2-3,拋物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在拋物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
图5-2-3
(1)若点C的纵坐标为2,求|MN|;
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
【解】 (1)拋物线y2=4x的准线l的方程为x=-1.
由点C的纵坐标为2,得点C的坐标为(1,2),
所以点C到准线l的距离d=2.又|CO|=,
所以|MN|=2=2=2.
(2)设C,则圆C的方程为2+(y-y0)2=+y,即x2-x+y2-2y0y=0.
由x=-1,得y2-2y0y+1+=0.
设M(-1,y1),N(-1,y2),则
由|AF|2=|AM|·|AN|,得|y1y2|=4,
所以+1=4,解得y0=±,此时Δ>0.所以圆心C的坐标为或,从而|CO|2=,
|CO|=,即圆C的半径为.
11.如图5-2-4,点F1(-c,0),F2(c,0)分别是椭圆C:+=1(a>b>0)的左、右焦点,过点F1作x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2的垂线交直线x=于点Q.
图5-2-4
(1)如果点Q的坐标是(4,4),求此时椭圆C的方程;
(2)证明:直线PQ与椭圆C只有一个交点.
【解】 (1)由条件知,P(-c,),故直线PF2的斜率为kPF2==-.
因为PF2⊥F2Q,所以直线F2Q的方程为y=x-,
故Q(,2a).
由题设知,=4,2a=4,解得a=2,c=1.
故椭圆方程为+=1.
(2)证明 直线PQ的方程为=,
即y=x+a.
将上式代入+=1得x2+2cx+c2=0,
解得x=-c,y=.
所以直线PQ与椭圆C只有一个交点.