- 2021-05-10 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏苏州中考数学试卷含答案
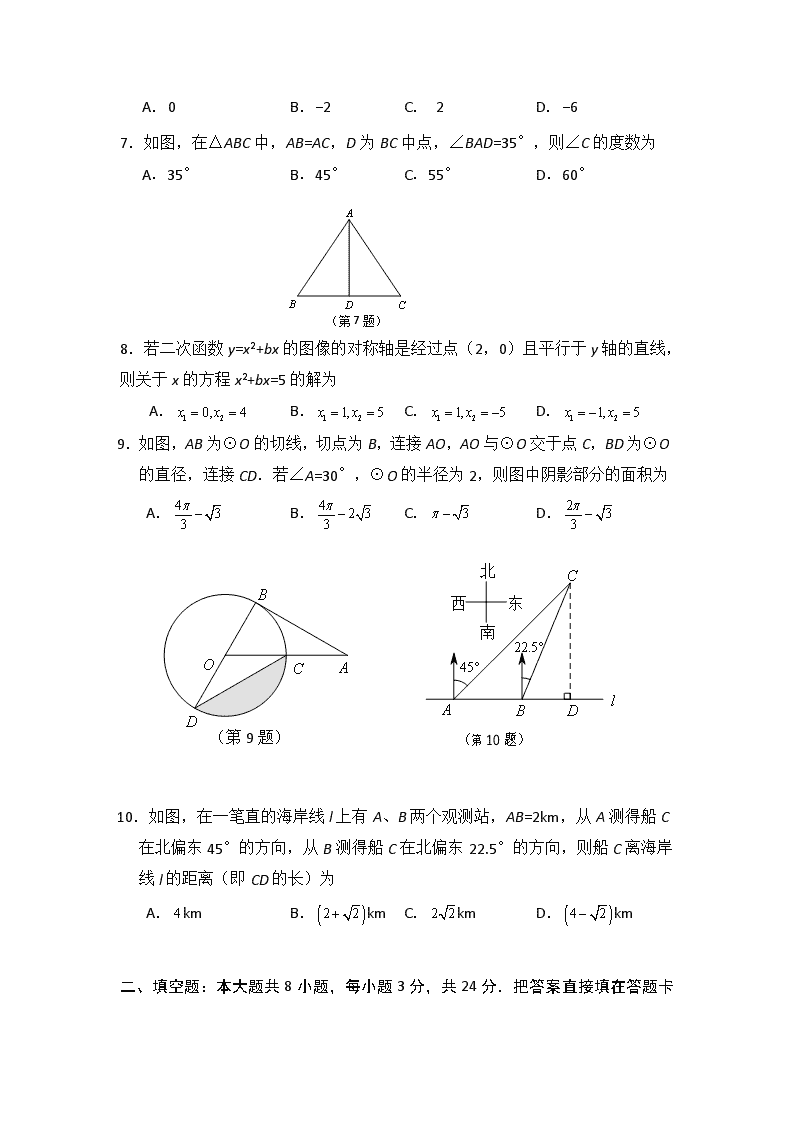
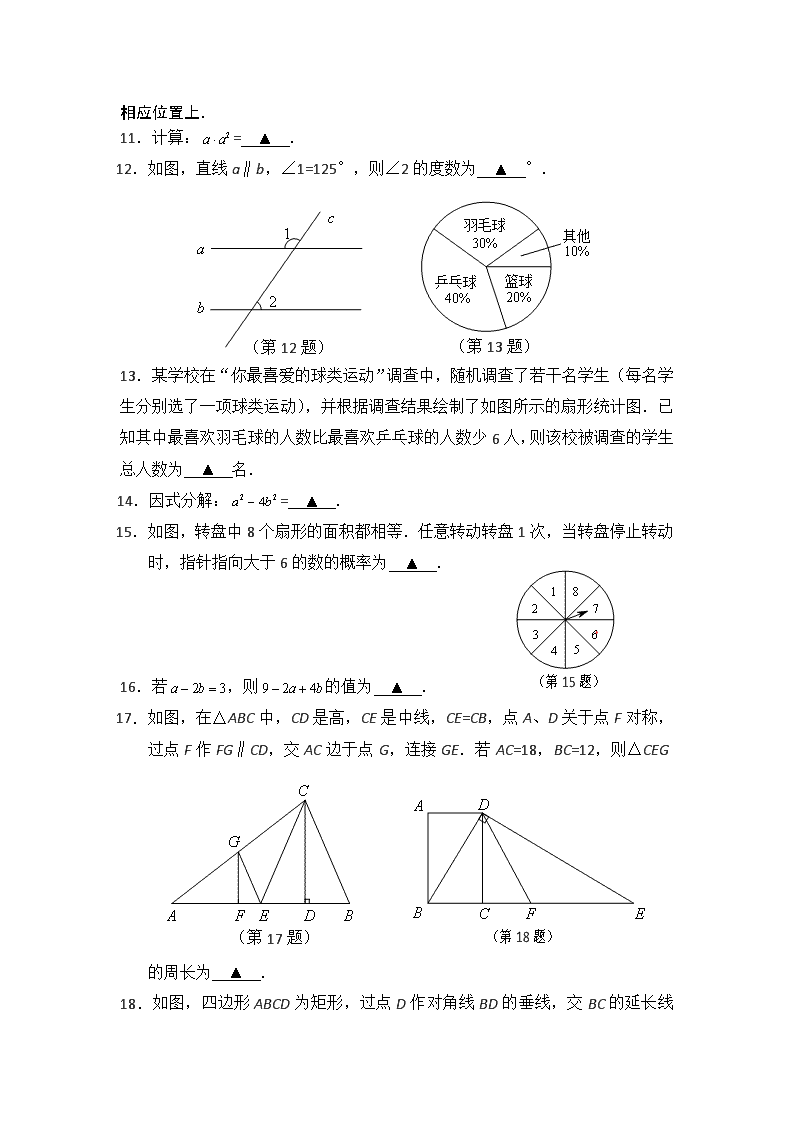
2015年苏州市初中毕业暨升学考试试卷 数 学 本试卷由选择题、填空题和解答题三大题组成,共28小题,满分130分,考试时间120分钟. 注意事项: 1.答题前,考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡相应位置上,并认真核对条形码上的准考号、姓名是否与本人的相符; 2.答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效,不得用其他笔答题; 3.考生答题必须答在答题卡上,保持卡面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效. 一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上. 1.2的相反数是 A.2 B. C.-2 D.- 2.有一组数据:3,5,5,6,7,这组数据的众数为 A.3 B.5 C.6 D.7 3.月球的半径约为1 738 000m,1 738 000这个数用科学记数法可表示为 A.1.738×106 B.1.738×107 C.0.1738×107 D.17.38×105 4.若,则有 A.0<m<1 B.-1<m<0 C.-2<m<-1 D.-3<m<-2 5.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表: 通话时间x/min 0<x≤5 5<x≤10 10<x≤15 15<x≤20 频数(通话次数) 20 16 9 5 则通话时间不超过15min的频率为 A.0.1 B.0.4 C.0.5 D.0.9 6.若点A(a,b)在反比例函数的图像上,则代数式ab-4的值为 A.0 B.-2 C. 2 D.-6 7.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为 A.35° B.45° C.55° D.60° (第7题) 8.若二次函数y=x2+bx的图像的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 A. B. C. D. 9.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为 A. B. C. D. (第9题) (第10题) 10.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为 A.km B.km C.km D.km 二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在 答题卡相应位置上. 11.计算:= ▲ . 12.如图,直线a∥b,∠1=125°,则∠2的度数为 ▲ °. (第12题) (第13题) 13.某学校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 ▲ 名. 14.因式分解:= ▲ . (第15题) 15.如图,转盘中8个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针指向大于6的数的概率为 ▲ . 16.若,则的值为 ▲ . (第17题) (第18题) 17.如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为 ▲ . 18.如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC 的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则的值为 ▲ . 三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔. 19.(本题满分5分) 计算:. 20.(本题满分5分) 解不等式组: 21.(本题满分6分) 先化简,再求值:,其中. 22.(本题满分6分)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗? 23.(本题满分8分) 一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀. (1)从中任意摸出1个球,恰好摸到红球的概率是 ▲ ; (2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率. 24.(本题满分8分)如图,在△ABC中,AB=AC.分别以B、C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD. (1)求证:AD平分∠BAC; (2)若BC=6,∠BAC=50°,求、的长度之和(结果保留). (第24题) 25.(本题满分8分)如图,已知函数(x>0)的图像经过点A、B,点B 的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图像经过点A、D,与x轴的负半轴交于点E. (第25题) (1)若AC=OD,求a、b的值; (2)若BC∥AE,求BC的长. 26.(本题满分10分)如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED. (1)求证:ED∥AC; (第26题) (2)若BD=2CD,设△EBD的面积为,△ADC的面积为,且,求△ABC的面积. 27.(本题满分10分)如图,已知二次函数(其中0<m <1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC. (1)∠ABC的度数为 ▲ °; (2)求P点坐标(用含m的代数式表示); (第27题) (3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由. 28.(本题满分10分)如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4), 半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置). (1)如图①,点P从A→B→C→D,全程共移动了 ▲ cm(用含a、b的代数式表示); (2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离; (第28题) (图②) (图①) (3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由. 2015年苏州市初中毕业暨升学考试 数学试题答案 一、选择题 1.C 2.B 3.A 4.C 5.D 6.B 7.C 8.D 9.A 10.B 二、填空题 11. 12.55 13.60 14. 15. 16.3 17.27 18.16 三、解答题 19.解:原式 = 3+5-1 = 7. 20.解:由,解得, 由,解得, ∴不等式组的解集是. 21.解:原式= =. 当时,原式=. 22.解:设乙每小时做x面彩旗,则甲每小时做(x+5)面彩旗. 根据题意,得. 解这个方程,得x=25.经检验,x=25是所列方程的解. ∴x+5=30. 答:甲每小时做30面彩旗,乙每小时做25面彩旗. 23.解:(1). (2)用表格列出所有可能的结果: 第二次 第一次 红球1 红球2 白球 黑球 红球1 (红球1,红球2) (红球1,白球) (红球1,黑球) 红球2 (红球2,红球1) (红球2,白球) (红球2,黑球) 白球 (白球,红球1) (白球,红球2) (白球,黑球) 黑球 (黑球,红球1) (黑球,红球2) (黑球,白球) 由表格可知,共有12种可能出现的结果,并且它们都是等可能的,其中 “两次都摸到红球”有2种可能. ∴P(两次都摸到红球)==. 24.证明:(1)由作图可知BD=CD. 在△ABD和△ACD中, ∴△ABD≌△ACD(SSS). ∴∠BAD=∠CAD,即AD平分∠BAC. 解:(2)∵AB=AC,ÐBAC=50°,∴∠ABC=∠ACB=65°. ∵BD= CD = BC,∴△BDC为等边三角形. ∴∠DBC=∠DCB=60°. ∴∠DBE=∠DCF=55°. ∵BC=6,∴BD= CD =6. ∴的长度=的长度=. ∴、的长度之和为. 25.解:(1)∵点B(2,2)在的图像上, ∴k=4,. ∵BD⊥y轴,∴D点的坐标为(0,2),OD=2. ∵AC⊥x轴,AC=OD,∴AC=3,即A点的纵坐标为3. ∵点A在的图像上,∴A点的坐标为(,3). ∵一次函数y=ax+b的图像经过点A、D, ∴ 解得 (2)设A点的坐标为(m,),则C点的坐标为(m,0). ∵BD∥CE,且BC∥DE,∴四边形BCED为平行四边形. ∴CE= BD=2. ∵BD∥CE,∴∠ADF=∠AEC. ∴在Rt△AFD中,tan∠ADF=, 在Rt△ACE中,tan∠AEC=, ∴,解得m=1. ∴C点的坐标为(1,0),BC=. 26.证明:(1)∵AD是△ABC的角平分线, ∴∠BAD =∠DAC. ∵∠E=∠BAD,∴∠E =∠DAC. ∵BE∥AD,∴∠E =∠EDA. ∴∠EDA =∠DAC. ∴ED∥AC. 解:(2)∵BE∥AD,∴∠EBD =∠ADC. ∵∠E =∠DAC, ∴△EBD∽△ADC,且相似比. ∴,即. ∵,∴,即. ∴. ∵,∴. 27.解:(1)45. 理由如下:令x=0,则y=-m,C点坐标为(0,-m). 令y=0,则,解得,. ∵0<m<1,点A在点B的左侧, ∴B点坐标为(m,0).∴OB=OC=m. ∵∠BOC=90°,∴△BOC是等腰直角三角形,∠OBC=45°. (2)解法一:如图①,作PD⊥y轴,垂足为D,设l与x轴交于点E, 由题意得,抛物线的对称轴为. 设点P坐标为(,n). ∵PA= PC, ∴PA2= PC2,即AE2+ PE2=CD2+ PD2. ∴. 解得.∴P点的坐标为. 解法二:连接PB. 由题意得,抛物线的对称轴为. ∵P在对称轴l上,∴PA=PB. ∵PA=PC,∴PB=PC. ∵△BOC是等腰直角三角形,且OB=OC, ∴P在BC的垂直平分线上. ∴P点即为对称轴与直线的交点. ∴P点的坐标为. (3)解法一:存在点Q满足题意. ∵P点的坐标为, ∴PA2+ PC2=AE2+ PE2+CD2+ PD2 =. ∵AC2=,∴PA2+ PC2=AC2.∴∠APC=90°. ∴△PAC是等腰直角三角形. ∵以Q、B、C为顶点的三角形与△PAC相似, ∴△QBC是等腰直角三角形. ∴由题意知满足条件的点Q的坐标为(-m,0)或(0,m). ①如图①,当Q点的坐标为(-m,0)时, 若PQ与x轴垂直,则,解得,PQ=. 若PQ与x轴不垂直, 则. ∵0<m<1,∴当时,取得最小值,PQ取得最小值. ∵<, ∴当,即Q点的坐标为(,0)时, PQ的长度最小. ②如图②,当Q点的坐标为(0,m)时, 若PQ与y轴垂直,则,解得,PQ=. 若PQ与y轴不垂直, 则. ∵0<m<1,∴当时,取得最小值,PQ取得最小值. ∵<, ∴当,即Q点的坐标为(0,)时, PQ的长度最小. 综上:当Q点坐标为(,0)或(0,)时,PQ的长度最小. 解法二: 如图①,由(2)知P为△ABC的外接圆的圆心. ∵∠APC 与∠ABC对应同一条弧,且∠ABC=45°, ∴∠APC=2∠ABC=90°. 下面解题步骤同解法一. 28.解:(1)a+2b. (2)∵在整个运动过程中,点P移动的距离为cm, 圆心O移动的距离为cm, 由题意,得. ① ∵点P移动2s到达B点,即点P用2s移动了bcm, 点P继续移动3s,到达BC的中点,即点P用3s移动了cm. ∴. ② 由①②解得 ∵点P移动的速度与⊙O 移动的速度相等, ∴⊙O 移动的速度为(cm/s). ∴这5s时间内圆心O移动的距离为5×4=20(cm). (3)存在这种情形. 解法一:设点P移动的速度为v1cm/s,⊙O移动的速度为v2cm/s, 由题意,得. 如图,设直线OO1与AB交于点E,与CD交于点F,⊙O1与AD相切于点G. 若PD与⊙O1相切,切点为H,则O1G=O1H. 易得△DO1G≌△DO1H,∴∠ADB=∠BDP. ∵BC∥AD,∴∠ADB=∠CBD. ∴∠BDP=∠CBD.∴BP=DP. 设BP=xcm,则DP=xcm,PC=(20-x)cm, 在Rt△PCD中,由勾股定理,可得, 即,解得. ∴此时点P移动的距离为(cm). ∵EF∥AD,∴△BEO1∽△BAD. ∴,即. ∴EO1=16cm.∴OO1=14cm. ①当⊙O首次到达⊙O1的位置时,⊙O移动的距离为14cm, ∴此时点P与⊙O移动的速度比为. ∵, ∴此时PD与⊙O1不可能相切. ②当⊙O在返回途中到达⊙O1的位置时,⊙O移动的距离为2×(20-4)-14=18(cm), ∴此时点P与⊙O移动的速度比为. ∴此时PD与⊙O1恰好相切. 解法二:∵点P移动的距离为cm(见解法一), OO1=14cm(见解法一),, ∴⊙O应该移动的距离为(cm). ①当⊙O首次到达⊙O1的位置时,⊙O移动的距离为14cm≠18 cm, ∴此时PD与⊙O1不可能相切. ②当⊙O在返回途中到达⊙O1的位置时,⊙O移动的距离为2×(20-4)-14=18(cm), ∴此时PD与⊙O1恰好相切. 解法三:点P移动的距离为cm,(见解法一) OO1=14cm,(见解法一) 由可设点P的移动速度为5k cm/s,⊙O的移动速度为4k cm/s, ∴点P移动的时间为(s). ①当⊙O首次到达⊙O1的位置时,⊙O移动的时间为, ∴此时PD与⊙O1不可能相切. ②当⊙O在返回途中到达⊙O1的位置时,⊙O移动的时间为, ∴此时PD与⊙O1恰好相切.查看更多