4月静安区中考数学二模试卷及答案

4月静安区中考数学二模试卷及答案

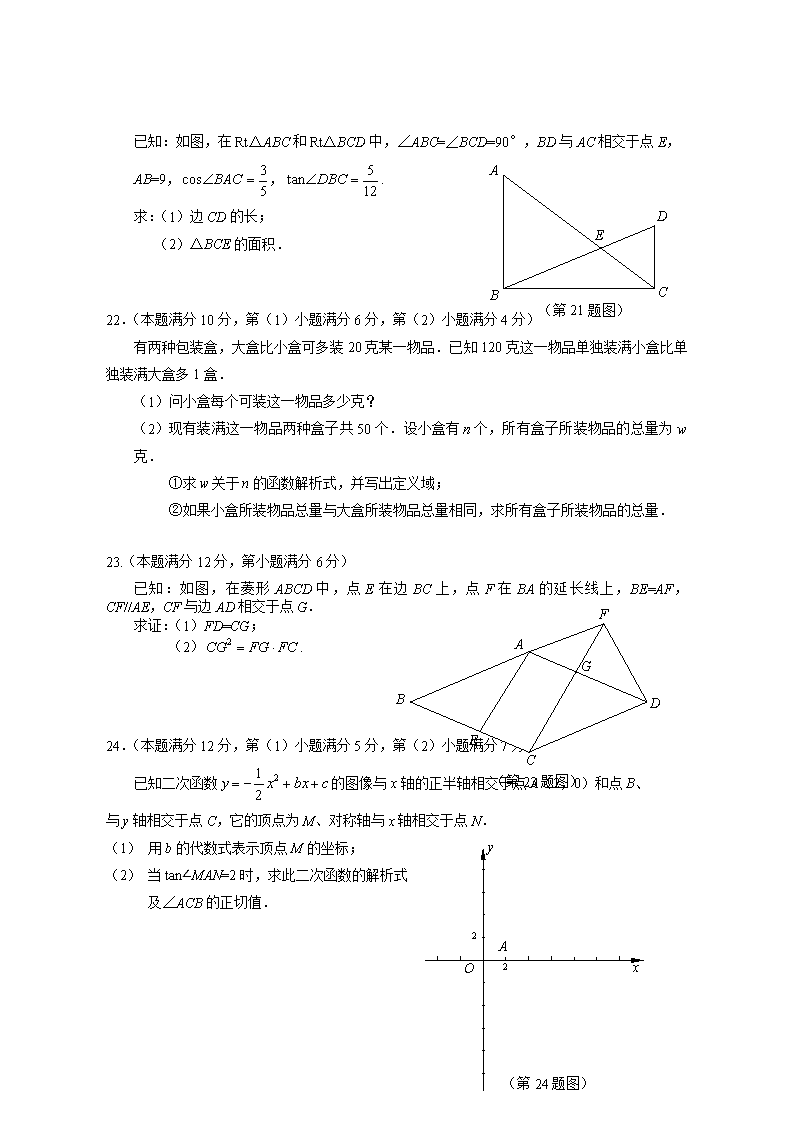
静安区2016学年第二学期期中教学质量调研 ‎ ‎ 九年级数学试卷 2017.4‎ ‎（满分150分，100分钟完成）‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本调研卷上答题一律无效．‎ ‎2．除第一、二大题外,其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎[每小题只有一个正确选项，在答题纸相应题号的选项上用2B铅笔正确填涂]‎ ‎1． 等于 ‎ ‎（A）； （B）； （C）； 　 （D）.‎ ‎2．下列二次根式里，被开方数中各因式的指数都为1的是 ‎ （A）； （B）； （C）； （D）．‎ ‎3．关于的一元二次方程的根的情况是 ‎（A）有两个不相等的实数根； （B）有两个相等的实数根； ‎ ‎（C）没有实数根； 　 （D）不能确定．‎ ‎4．一次数学作业共有10道题目，某小组8位学生做对题目数的情况如下表：‎ 做对题目数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 人数 ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎ 那么这8位学生做对题目数的众数和中位数分别是 ‎（A）9和8； （B）9和8.5 ； （C）3和2； （D）3和1．‎ ‎5．在下列图形中，一定是中心对称图形，但不一定是轴对称图形的为 ‎（A）正五边形； （B）正六边形； （C）等腰梯形； （D）平行四边形．‎ ‎6．已知四边形ABCD中，对角线AC与BD相交于点O，AD//BC ，下列判断中错误的是 ‎ （A）如果AB=CD，AC＝BD，那么四边形ABCD是矩形；‎ ‎ （B）如果AB//CD，AC＝BD，那么四边形ABCD是矩形；‎ ‎ （C）如果AD=BC，AC⊥BD，那么四边形ABCD是菱形；‎ ‎ （D）如果OA=OC，AC⊥BD，那么四边形ABCD是菱形.‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎[在答题纸相应题号后的空格内直接填写答案]‎ ‎7．计算：  ▲ ．‎ ‎8．在实数范围内分解因式：  ▲ ． ‎ ‎9．不等式组的解集是  ▲ ．‎ ‎10．函数的定义域是 ▲ ．‎ ‎11．如果函数的图像在每个象限内，当自变量的值逐渐增大时，的值随着逐渐增大，那么的取值范围是 ▲ ． ‎ ‎0.01‎ ‎0.02‎ ‎0.03‎ ‎0.04‎ 体重（千克）‎ ‎40 45 50 55 60 65 70‎ ‎12．如果实数满足，那么的值是 ▲ ．‎ ‎13．为了解全区5000名初中毕业生的体重情况，随机抽 ‎ 测了400名学生的体重，频率分布如图所示（每小 ‎ 组数据可含最小值，不含最大值），其中从左至右前 ‎ 四个小长方形的高依次为0.02、0.03、0.04、0.05， ‎ ‎（第13题图）‎ ‎ 由此可估计全区初中毕业生的体重不小于60千克 ‎（第15题图）‎ A B C D ‎ 的学生人数约为 ▲ 人．‎ ‎14．布袋里有三个红球和两个白球，它们除了颜色外其他都相同，‎ ‎ 从布袋里摸出两个球，摸到两个红球的概率是 ▲ ．‎ A B C D E F ‎（第16题图）‎ ‎15．如图，在△ABC中，点D是边AC的中点，如果，‎ ‎ 那么 ▲ （用向量表示）．‎ ‎16．如图，在正方形ABCD中，点E、F分别在边BC、CD上，‎ ‎（第18题图）‎ A B ‎ △AEF是等边三角形，如果AB=1，那么CE的长是 ▲ ．‎ ‎17. 在Rt△ABC中，∠C＝90°，∠B=70°，点D在边AB上， ‎ ‎ △ABC绕点D旋转后点B与点C重合，点C落在点C’， ‎ ‎ 那么∠ACC’的度数是 ▲ ．‎ ‎18．如图，⊙A和⊙B的半径分别为5和1，AB＝3，点O在直线 ‎　　AB上，⊙O与⊙A、⊙B都内切，那么⊙O半径是 ▲ ．‎ 三、解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答题纸的相应位置上]‎ ‎19．（本题满分10分） ‎ ‎ 化简：（－），并求时的值． ‎ ‎20．（本题满分10分）‎ ‎ 解方程：‎ ‎21．（本题满分10分，每小题满分5分） ‎ E A C B D ‎（第21题图）‎ 已知：如图，在Rt△ABC和Rt△BCD中，∠ABC=∠BCD=90°，BD与AC相交于点E，‎ AB=9，，.‎ 求：（1）边CD的长；‎ ‎（2）△BCE的面积．‎ ‎22．（本题满分10分，第（1）小题满分6分，第（2）小题满分4分） ‎ 有两种包装盒，大盒比小盒可多装20克某一物品．已知120克这一物品单独装满小盒比单独装满大盒多1盒．‎ （1） 问小盒每个可装这一物品多少克？ ‎ （2） 现有装满这一物品两种盒子共50个．设小盒有个，所有盒子所装物品的总量为克．‎ ‎ ①求关于的函数解析式，并写出定义域；‎ ‎ ②如果小盒所装物品总量与大盒所装物品总量相同，求所有盒子所装物品的总量．‎ ‎23.（本题满分12分，第小题满分6分）‎ ‎（第23题图）‎ E D C G F A B ‎ 已知：如图，在菱形ABCD中，点E在边BC上，点F在BA的延长线上，BE=AF，CF//AE，CF与边AD相交于点G．‎ ‎ 求证：（1）FD=CG；‎ ‎ （2）.‎ ‎24．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）‎ 已知二次函数的图像与x轴的正半轴相交于点A（2，0）和点B、‎ ‎（第24题图）‎ A O x ‎ 2‎ y ‎ 2‎ 与y轴相交于点C，它的顶点为M、对称轴与x轴相交于点N．‎ ‎（1） 用b的代数式表示顶点M的坐标；‎ ‎（2） 当tan∠MAN=2时，求此二次函数的解析式 ‎ 及∠ACB的正切值．‎ ‎25．（本题满分14分，第（1）小题满分6分，第（2）小题满分8分）‎ ‎ 如图，已知⊙O的半径OA的长为2，点B是⊙O上的动点，以AB为半径的⊙A与线段OB相交于点C，AC的延长线与⊙O相交于点D．设线段AB的长为x, 线段OC的长为y.‎ ‎ （1）求y关于x的函数解析式，并写出定义域；‎ ‎ （2）当四边形ABDO是梯形时，求线段OC的长．‎ ‎（第25题图）‎ A B D O C ‎ ‎ 静安区质量调研九年级数学试卷参考答案及评分标准2017.4.20‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．C； 2．B； 3．A； 4．B； 5．D； 6．A．‎ 二．填空题：（本大题共12题，满分48分）‎ ‎ 7．； 8．； 9．； ‎ ‎ 10．； 11．； 12．2；‎ ‎ 13．1500； 14．； 15．； ‎ ‎ 16．； 17．50°； 18．或． ‎ 三、（本大题共7题, 第19~22题每题10分, 第23、24题每题12分, 第25题14分, 满分78分）‎ ‎19．解：原式=……………………………………（3分）‎ ‎ =……………………………………（2分）‎ ‎ =．…………………………………………………………………………（2分）‎ ‎ 当时，…………………………………………………………（1分）‎ ‎ 原式==．……………………………………………………………………（2分）‎ ‎20．解：，………………………………………………………………（1分）‎ ‎，…………………………………………………………（2分）‎ ‎．………………………………………………………………………（1分）‎ ‎，………………………………………………………………（2分）‎ ‎，……………………………………………………………………（1分）‎ ‎，………………………………………………………………………（1分）‎ 经检验：都是增根，………（1分）所以原方程无解．…………（1分）‎ ‎21．解：（1）在Rt△ABC中，．………………………………………（1分）‎ ‎∴，………………………………………………………………（1分）‎ ‎ ∴BC=．…………………………………………（1分）‎ 在Rt△BCD中，，………………………………………（1分）‎ ‎ ∴CD=5．…………………………………………………………………………（1分）‎ ‎ （2）过点E作EH⊥BC，垂足为H，…………………………………………………（1分）‎ ‎∵∠ABC=∠BCD=90°，∴∠ABC+∠BCD=180°，∴CD//AB．‎ ‎∴．………………………………………………………………（1分）‎ ‎ ∵∠EHC=∠ABC=90°，∴EH//AB，∴．…………………（1分）‎ ‎ ∴．…………………………………………………（1分）‎ ‎ ∴．……………………………………（1分）‎ ‎22．解：（1）设小盒每个可装这一物品克，…………………………………………………（1分）‎ ‎ ∴，…………………………………………………………………（2分）‎ ‎ ，……………………………………………………………（1分）‎ ‎ ，………………………………………………………………（1分）‎ ‎ 　它们都是原方程的解，但不合题意．∴小盒每个可装这一物品40克．（1分）‎ ‎ （2）①，（为整数）…………（2分）‎ ‎ ②，，.…………………………………（2分）‎ ‎ ∴所有盒子所装物品的总量为2400克．‎ ‎23．证明：（1）∵在菱形ABCD中，AD//BC，∴∠FAD=∠B，……………………………（1分）‎ 又∵AF=BE，AD=BA，∴△ADF≌△BAE．……………………………………（2分）‎ ‎∴FD＝EA，…………………………………………………………………………（1分）‎ ‎∵CF//AE，AG//CE,∴EA=CG．…………………………………………………（1分）‎ ‎∴FD=CG．…………………………………………………………………………（1分）‎ ‎（2）∵在菱形ABCD中，CD//AB，∴∠DCF=∠BFC．……………………………（1分）‎ ‎　　　∵CF//AE，∴∠BAE=∠BFC，∴∠DCF=∠BAE．……………………………（1分）‎ ‎∵△ADF≌△BAE，∴∠BAE＝∠FDA，∴∠DCF＝∠FDA．…………………（1分）‎ 又∵∠DFG＝∠CFD，∴△FDG∽△FCD．……………………………………（1分）‎ ‎∴，．…………………………………………………（1分）‎ ‎∵FD=CG，．……………………………………………………（1分）‎ ‎24．解：（1）∵二次函数的图像经过点A（2，0），‎ ‎　　　　∴，………………………………………………………………（1分）‎ ‎ ∴，…………………………………………………………………………（1分）‎ ‎∴，………（2分）‎ ‎∴顶点M的坐标为（，）．……………………………………………（1分）‎ ‎　（2）∵tan∠MAN=2，∴MN=2AN．………………………………………………（1分）‎ ‎　 ∵M（，），∴ N（，0），．……（1分）‎ ‎ ①当点B在点N左侧时， AN=，∴，．‎ ‎ 不符合题意．…………………………………………………………………………（1分）‎ ‎ ②当点B在点N右侧时， AN=， ∴，．…………（1分）‎ ‎∴二次函数的解析式为．………………………………………（1分）‎ ‎∴点C（0，–10），∵点A、B关于直线MN对称，∴点B（10，0）．‎ ‎∵OB=OC=10，∴BC=10，∠OBC＝45°．………………………………………（1分）‎ 过点A作AH⊥BC,垂足为H，∵AB＝8，∴AH=BH=4，∴CH＝6．‎ ‎ ∴．……………………………………………………（1分）‎ ‎25．解：（1）在⊙O与⊙A中，∵OA=OB，AB=AC，∴∠ACB ＝∠ABC=∠OAB．……（2分）‎ ‎∴△ABC∽△OAB．…………………………………………………………………（1分）‎ ‎∴，∴，………………………………………………………（1分）‎ ‎∴，∵OC=OB–BC，∴y关于x的函数解析式，……（1分）‎ 定义域为．………………………………………………………………（1分）‎ ‎（2）①当OD//A B时，∴，∴，……………………………（1分）‎ ‎ ∴，∴，……………………………………………（1分）‎ ‎ ∴（负值舍去）．……………………………………………………（1分）‎ ‎ ∴AB=，这时ABOD，符合题意.‎ ‎　　　∴OC=．………………………………………（1分）‎ ‎ ②当BD//OA时，设∠ODA=，∵BD//OA，OA=OD，∴∠BDA=∠OAD=∠ODA=，‎ ‎ 又∵OB=OD，∴∠BOA＝∠OBD=∠ODB＝.…………………………………（1分）‎ ‎　　∵AB=AC，OA＝OB，∴∠OAB＝∠ABC=∠ACB=∠COA+∠CAO＝．………（1分）‎ ‎　　∵∠AOB+∠OAB＋∠OBA=180°，∴，‎ ‎ ∴，∠BOA＝45°．………………………………………………………（1分）‎ ‎ ∴∠ODB=∠OBD=45°，∠BOD=90°，∴BD=. ∵BD//OA，∴．‎ ‎ ∴，∴．．………………………………（1分）‎ ‎ 由于BDOA，符合题意.‎ ‎ ∴当四边形ABDO是梯形时，线段OC的长为或．‎ 或：过点B作BH⊥OA，垂足为H， BH=OH=，AH=2–，‎ ‎ ∴.‎ ‎ ∴.…………………………（1分）‎