中考复习专题平行四边形综合题

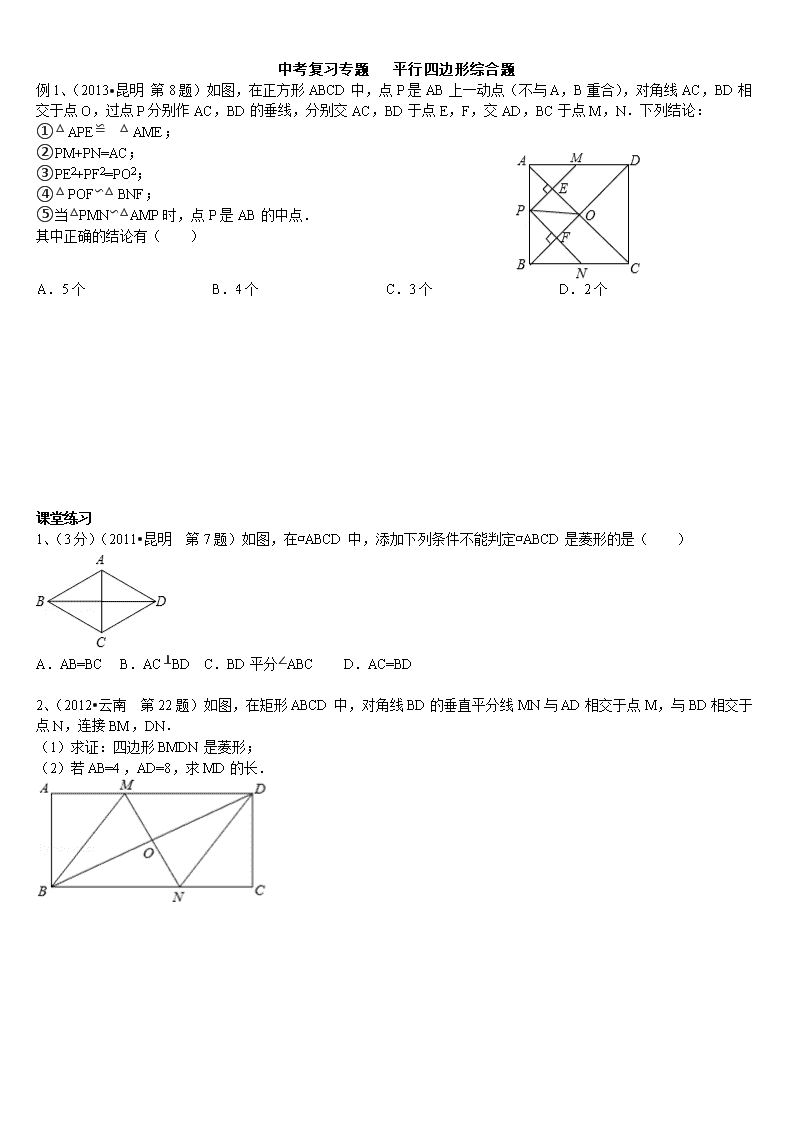
中考复习专题平行四边形综合题

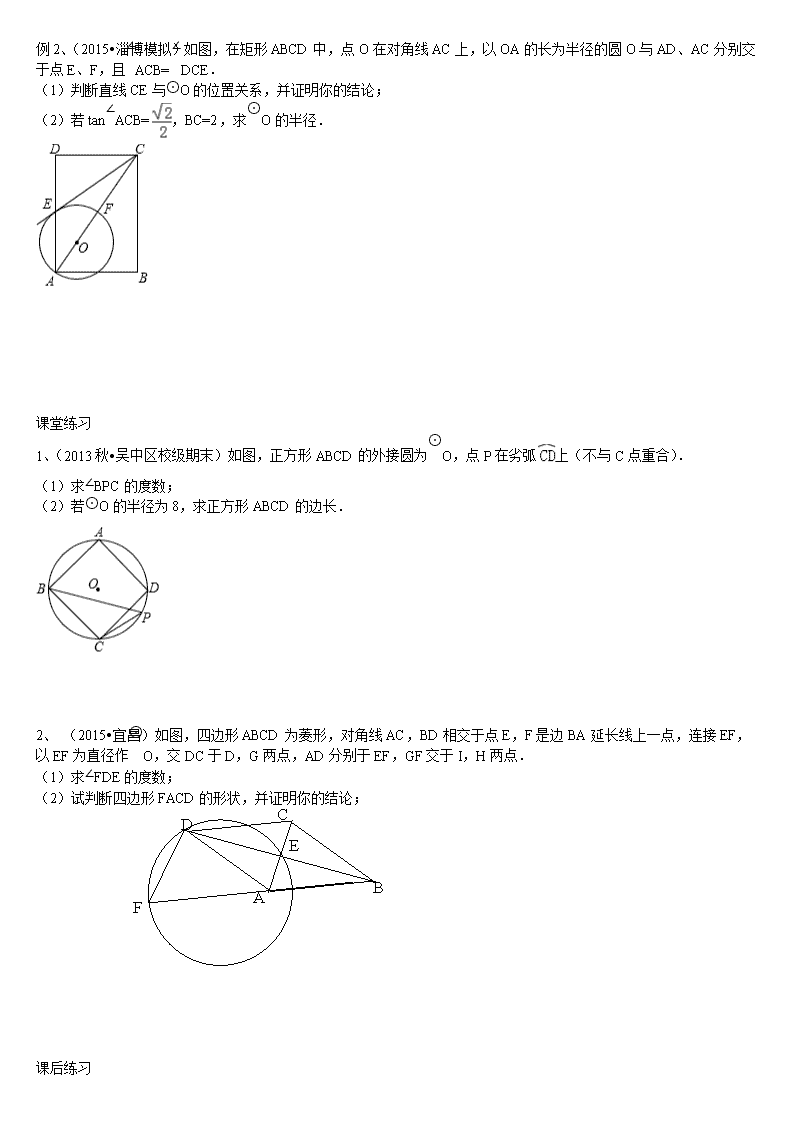
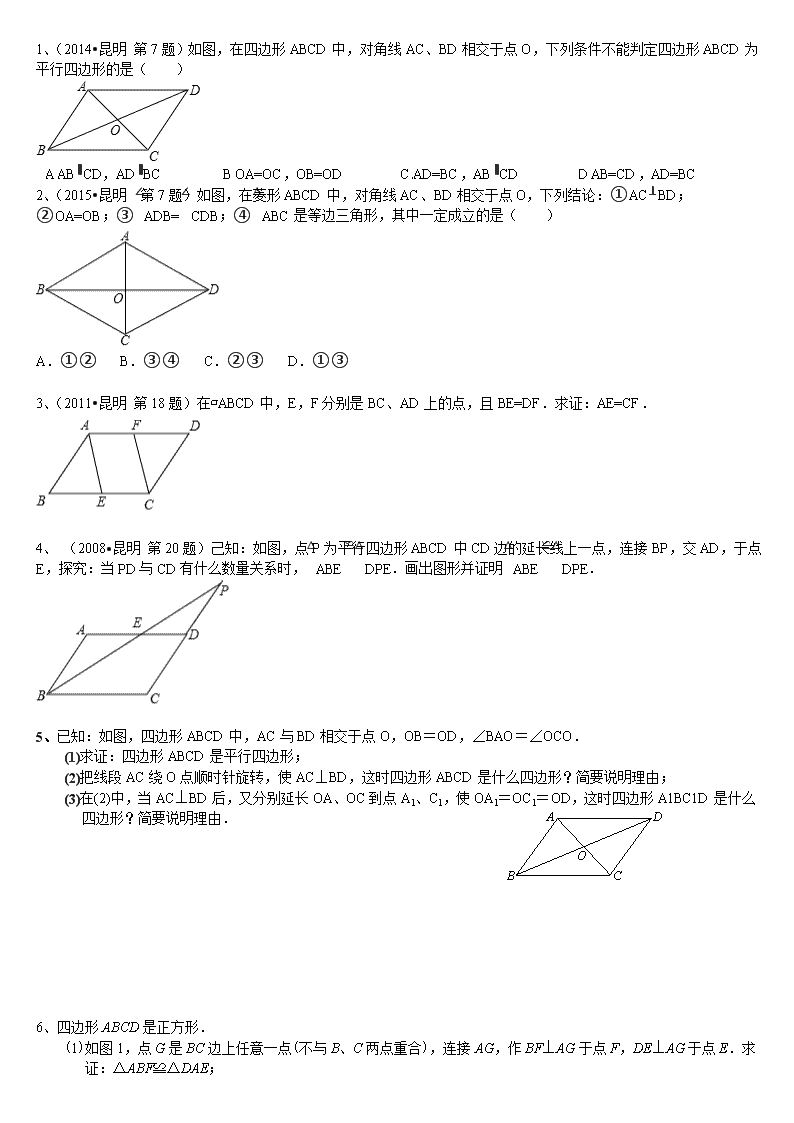
‎ ‎ 中考复习专题 平行四边形综合题 例1、（2013•昆明 第8题）如图，在正方形ABCD中，点P是AB上一动点（不与A，B重合），对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N．下列结论：‎ ‎①△ APE≌ △ AME；‎ ‎②PM+PN=AC；‎ ‎③PE2+PF2=PO2；‎ ‎④△ POF∽△ BNF；‎ ‎⑤当△PMN∽△AMP时，点P是AB的中点．‎ 其中正确的结论有（　　）‎ ‎　‎ A．‎ ‎5个 B．‎ ‎4个 C．‎ ‎3个 D．‎ ‎2个 课堂练习 ‎1、（3分）（2011•昆明 第7题）如图，在▱ABCD中，添加下列条件不能判定▱ABCD是菱形的是（　　）‎ A．AB=BC B．AC⊥BD C．BD平分∠ABC D．AC=BD ‎ ‎2、（2012•云南 第22题）如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点N，连接BM，DN．‎ ‎（1）求证：四边形BMDN是菱形；‎ ‎（2）若AB=4，AD=8，求MD的长．‎ 例2、（2015•淄博模拟）如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F，且∠ACB=∠DCE．‎ ‎（1）判断直线CE与⊙O的位置关系，并证明你的结论；‎ ‎（2）若tan∠ACB=，BC=2，求⊙O的半径．‎ 课堂练习 ‎1、（2013秋•吴中区校级期末）如图，正方形ABCD的外接圆为⊙O，点P在劣弧上（不与C点重合）．‎ ‎（1）求∠BPC的度数；‎ ‎（2）若⊙O的半径为8，求正方形ABCD的边长．‎ ‎　‎ ‎2、 （2015•宜昌）如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别于EF，GF交于I，H两点．‎ ‎（1）求∠FDE的度数；‎ ‎（2）试判断四边形FACD的形状，并证明你的结论；‎C D E A B F B A F 课后练习 ‎1、（2014•昆明 第7题）如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（　　）‎ ‎　‎ A．‎ AB∥CD，AD∥BC B．‎ OA=OC，OB=OD C．‎ AD=BC，AB∥CD D．‎ AB=CD，AD=BC ‎2、（2015•昆明 第7题）如图，在菱形ABCD中，对角线AC、BD相交于点O，下列结论：①AC⊥BD；②OA=OB；③∠ADB=∠CDB；④△ABC是等边三角形，其中一定成立的是（　　）‎ A．①② B．③④ C．②③ D．①③‎ ‎3、（2011•昆明 第18题）在▱ABCD中，E，F分别是BC、AD上的点，且BE=DF．求证：AE=CF．‎ ‎4、 （2008•昆明 第20题）己知：如图，点P为平行四边形ABCD中CD边的延长线上一点，连接BP，交AD，于点E，探究：当PD与CD有什么数量关系时，△ABE≌△DPE．画出图形并证明△ABE≌△DPE．‎ ‎5、已知：如图，四边形ABCD中，AC与BD相交于点O，OB＝OD，∠BAO＝∠OCO．‎ ‎(1)求证：四边形ABCD是平行四边形；‎ ‎(2)把线段AC绕O点顺时针旋转，使AC⊥BD，这时四边形ABCD是什么四边形？简要说明理由；‎ A D B C O ‎(3)在(2)中，当AC⊥BD后，又分别延长OA、OC到点A1、C1，使OA1＝OC1＝OD，这时四边形A1BC1D是什么四边形？简要说明理由．‎ ‎6、四边形ABCD是正方形．‎ ‎(1)如图1，点G是BC边上任意一点(不与B、C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证：△ABF≌△DAE；‎ ‎(2)在(1)中，线段EF与AF、BF的等量关系是 (直接写出结论即可，不需要证明)；‎ ‎(3)如图2，点G是CD边上任意一点(不与C、D两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．那么图中全等三角形是 ，线段EF与AF、BF的等量关系是 (直接写出结论即可，不需要证明)．‎ A A B B C D E F G C D G E F 图1‎ 图2‎ ‎7、已知：如图，在梯形ABCD中，AD∥BC，∠DCB = 90°，E是AD的中点，点P是BC边上的动点（不与点B重合），EP与BD相交于点O.‎ ‎（1）当P点在BC边上运动时，求证：△BOP∽△DOE；‎ ‎（2）设（1）中的相似比为，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形？①当= 1时，是 ；②当= 2时，是 ；③当= 3时，是 . 并证明= 2时的结论.‎ A B C D E P O