2010中考数学专题复习——反比例函数

2010中考数学专题复习——反比例函数

中考数学专题复习——反比例函数 一、选择题 ‎1. (08浙江温州)已知反比例函数的图象经过点，则的值是（ ）‎ A． B．‎6 ‎ C． D．‎ ‎2.(2008山东烟台)在反比例函数的图象上有两点A，B，当时，有，则的取值范围是（ ）‎ A、 B、 C、 D、‎ ‎3.(2008浙江宁波)如图，正方形的边长为2，反比例函数过点，‎ 则的值是（ ）‎ A． B． C． D．‎ x y C O A B ‎4.（2008年山东省临沂市）如图，直线与双曲线交于A、B两点，若A、B两点的坐标分别为A，B，则与的值为（ ）‎ A． －8 B． ‎4 C． －4 D． 0‎ ‎ 5.(2008年辽宁省十二市)若反比例函数的图象经过点，则这个函数的图象一定经过点（ ）‎ A． B． C． D．‎ ‎6.(2008年沈阳市)下列各点中，在反比例函数图象上的是（ ） ‎ A． B． C． D．‎ ‎7.（2008年湖南省邵阳市）若反比例函数的图象经过点，则这个函数的图象一定经过点（ ）‎ A． B． C． D．‎ ‎8．（2008湖北黄冈）已知反比例函数，下列结论中，不正确的是（ ）‎ A．图象必经过点 B．随的增大而减少 C．图象在第一、三象限内 D．若，则 ‎9．(2008湖南株洲)已知函数的图象如下，当时，的取值范围是（　　　）‎ A． B． ‎ C． 或 D．或 ‎-1‎ ‎-1‎ y x O ‎10．(2008黑龙江哈尔滨)已知反比例函数y＝的图象位于第一、第三象限，则k的取值范围是（ ）．‎ ‎ （A）k＞2 （B） k≥2 ‎ ‎ （C）k≤2 （D） k＜2‎ ‎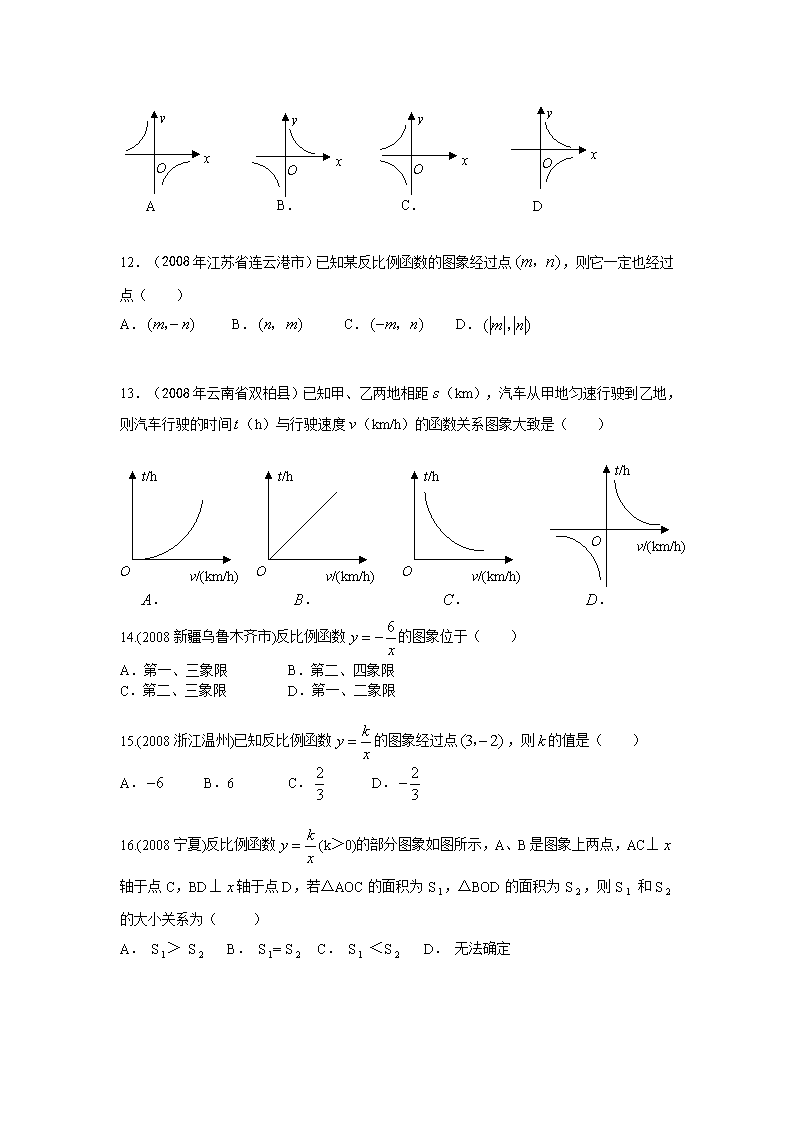11．（2008年山东省青岛市）如果点和点是直线上的两点，且当时，，那么函数的图象大致是（ ）‎ y x O y x O y x O y x O A．‎ B．‎ C．‎ D．‎ ‎12．（2008年江苏省连云港市）已知某反比例函数的图象经过点，则它一定也经过点（ ）‎ A． B． C． D．‎ ‎13．（2008年云南省双柏县）已知甲、乙两地相距（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间（h）与行驶速度（km/h）的函数关系图象大致是（ ）‎ t/h v/(km/h)‎ O t/h v/(km/h)‎ O t/h v/(km/h)‎ O t/h v/(km/h)‎ O A．‎ B．‎ C．‎ D．‎ ‎14.(2008新疆乌鲁木齐市)反比例函数的图象位于（ ）‎ A．第一、三象限 B．第二、四象限 C．第二、三象限 D．第一、二象限 ‎15.(2008浙江温州)已知反比例函数的图象经过点，则的值是（ ）‎ A． B．‎6 ‎ C． D． ‎ ‎16.(2008宁夏)反比例函数(k＞0)的部分图象如图所示，A、B是图象上两点，AC⊥轴于点C，BD⊥轴于点D，若△AOC的面积为S，△BOD的面积为S，则S和S 的大小关系为（ ）‎ A． S＞ S B． S= S C． S ＜S D． 无法确定 ‎17．（2008湖南益阳市）物理学知识告诉我们，一个物体所受到的压强P与所受压力F及受力面积S之间的计算公式为. 当一个物体所受压力为定值时，那么该物体所受压强P与受力面积S之间的关系用图象表示大致为（ ）‎ O P S S O P O P S O P A B C D S ‎18．（2008湖南常德市）下面的函数是反比例函数的是 （ ）‎ ‎ A． B． ‎ ‎ C． D．‎ ‎19．（2008年浙江省嘉兴市）某反比例函数的图象经过点，则此函数图象也经过点（ ）‎ A． B． C． D．‎ ‎20。（2008江苏南京）已知反比例函数的图像经过点P（－2，1），则这个函数的图像位于（ ）‎ ‎ A.第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限 ‎21．（2008山东济南）如图：等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线y=（k≠0），与△ABC有交点，则k的取值范围是（ ）A.10)与直线y=k′x交于A，B两点，点A在第一象限.试解答下列问题：(1)若点A的坐标为(4，2).则点B的坐标为 ；若点A的横坐标为m，则点B的坐标可表示为 ；‎ ‎（2）如图2，过原点O作另一条直线l，交双曲线y=(k>0)于P，Q两点，点P在第一象限.①说明四边形APBQ一定是平行四边形；②设点A.P的横坐标分别为m，n，四边形APBQ可能是矩形吗?可能是正方形吗?若可能，直接写出mn应满足的条件；若不可能，请说明理由. ‎ x y B A O 图1‎ ‎3.(2008浙江义乌)已知：等腰三角形OAB在直角坐标系中的位置如图，点A的坐标为（），点B的坐标为（－6，0）.‎ ‎（1）若三角形OAB关于y轴的轴对称图形是三角形O，‎ 请直接写出A、B的对称点的坐标；‎ ‎（2）若将三角形沿x轴向右平移a个单位，此时点A 恰好落在反比例函数的图像上，求a的值；‎ ‎（3）若三角形绕点O按逆时针方向旋转度（）.‎ ‎①当=时点B恰好落在反比例函数的图像上，求k的值．‎ ‎②问点A、B能否同时落在①中的反比例函数的图像上，若能，求出 的值；若不能，请说明理由.‎ ‎4．（2008山东威海）如图，点A（m，m＋1），B（m＋3，m－1）都在反比例函数的图象上． ‎ x O y A B ‎（1）求m，k的值； ‎ ‎（2）如果M为x轴上一点，N为y轴上一点， ‎ 以点A，B，M，N为顶点的四边形是平行四边形， ‎ 友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．　 ‎ 试求直线MN的函数表达式． ‎ ‎（3）选做题：在平面直角坐标系中，点P的坐标 为（5，0），点Q的坐标为（0，3），把线段PQ向右平 移4个单位，然后再向上平移2个单位，得到线段P1Q1，‎ 则点P1的坐标为 ，点Q1的坐标为 ．‎ x O y ‎1‎ ‎2‎ ‎3‎ ‎1‎ Q P ‎2‎ P1‎ Q1‎ ‎ ‎ ‎5. （2008年山东省滨州市）（1）探究新知：‎ 如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由.‎ ‎（2）结论应用：‎ ‎①如图2，点M、N在反比例函数y=的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F.‎ 试应用（1）中得到的结论证明：MN∥EF.‎ ‎②若①中的其他条件不变，只改变点M，N的位置如图3所示，‎ 请判断MN与E是否平行.‎ ‎6.(2008年天津市)已知点P（2，2）在反比例函数（）的图象上，‎ ‎（Ⅰ）当时，求的值；‎ ‎（Ⅱ）当时，求的取值范围．‎ ‎7.（2008年四川巴中市）为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量（mg）与燃烧时间（分钟）成正比例；燃烧后，与成反比例（如图所示）．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．据以上信息解答下列问题：‎ ‎（1）求药物燃烧时与的函数关系式．‎ ‎（2）求药物燃烧后与的函数关系式．‎ ‎（3）当每立方米空气中含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，经多长时间学生才可以回教室？‎ ‎8.(2008年成都市)如图，已知反比例函数y = 的图象经过点A（1，- 3），一次函数y = kx + b的图象经过点A与点C（0，- 4），且与反比例函数的图象相交于另一点B.‎ ‎（1）试确定这两个函数的表达式；‎ ‎（2）求点B的坐标.‎ ‎9.(2008年乐山市)题乙：图（14）是反比例函数的图象，当－4≤x≤－1时，－4≤y≤－1‎ （1） 求该反比例函数的解析式 （2） 若M、N分别在反比例函数图象的两支上，请指出什么情况下线段MN最短（不需证明），并求出线段MN长度的取值范围 M N x y o ‎-4‎ ‎-4‎ ‎-1‎ ‎-1‎ ‎10.(2008年大庆市)如图，反比例函数的图象与一次函数的图象相交于两点，．（1）分别求出反比例函数与一次函数的函数关系式；‎ ‎（2）若直线与轴交于点，求的面积．‎ y x O A B C ‎11.（2008江苏淮安）某项工程需要沙石料2×lO6立方米，阳光公司承担了该工程运送沙石料的任务．‎ ‎ (1)在这项任务中平均每天的工作量v(立方米／天)与完成任务所需要的时间t(天)之间具有怎样的函数关系?写出这个函数关系式．‎ ‎ (2)阳光公司计划投入A型卡车200辆，每天一共可以运送沙石料2×104立方米，则完成全部运送任务需要多少天?如果工作了25天后，由于工程进度的需要，公司准备再投入A型卡车120辆,在保持每辆车每天工作量不变的前提下，问：是否能提前28天完成任务?‎ ‎12.（2008广州市）如图8，一次函数的图象与反比例函数的图象相交于A、B两点 ‎（1）根据图象，分别写出A、B的坐标；‎ ‎（2）求出两函数解析式；‎ ‎（3）根据图象回答：当为何值时，‎ 一次函数的函数值大于反比例函数的函数值 图8‎ ‎13.（2008四川达州市）A B O C y x l 20．（6分）平行于直线的直线不经过第四象限，且与函数和图象交于点，过点作轴于点，轴于点，四边形的周长为8．求直线的解析式．‎ ‎ ‎ 图3‎ ‎14.（2008山西太原）人的视觉机能受运动速度的影响很大，行驶中司机在驾驶室内观察前方物体时是动态的，车速增加，视野变窄。当车速为‎50km/h时，视野为80度。如果视野f（度）是车速v（km/h）的反比例函数，求f，v之间的关系式，并计算当车速为‎100 km/h时视野的度数。‎ ‎15.(2008 山东 聊城)已知一次函数与反比例函数的图象交于点．‎ ‎（1）求这两个函数的函数关系式；‎ ‎（2）在给定的直角坐标系（如图）中，画出这两个函数的大致图象；‎ ‎（3）当为何值时，一次函数的值大于反比例函数的值？当为何值时，一次函数的值小于反比例函数的值？‎ O ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎6‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-5‎ ‎-6‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-5‎ ‎-6‎ x y ‎16．（2008年江苏省苏州市）如图，帆船和帆船在太湖湖面上训练，为湖面上的一个定点，教练船静候于点．训练时要求两船始终关于点对称．以为原点，建立如图所示的坐标系，轴，轴的正方向分别表示正东、正北方向．设两船可近似看成在双曲线上运动．湖面风平浪静，双帆远影优美．训练中当教练船与两船恰好在直线上时，三船同时发现湖面上有一遇险的船，此时教练船测得船在东南方向上，船测得与的夹角为，船也同时测得船的位置（假设船位置不再改变，三船可分别用三点表示）．‎ ‎（1）发现船时，三船所在位置的坐标分别为和；‎ ‎（2）发现船，三船立即停止训练，并分别从三点出发船沿最短路线同时前往救援，设两船的速度相等，教练船与船的速度之比为，问教练船是否最先赶到？请说明理由．‎ y x A　‎ B　‎ O　‎ ‎1　‎ ‎1　‎ ‎　‎ ‎　‎ C　‎ ‎(百米)　‎ ‎(百米)　‎ ‎17．（2008湖南郴州）．已知一次函数y=ax＋b的图像与反比例函数 的图像交于A（2，2），B(－1，m)，求一次函数的解析式 ‎18．（2008江苏宿迁）如图，已知反比例函数的图象与一次函数的图象交于、两点，．‎ ‎(1)求反比例函数和一次函数的关系式；‎ ‎(2)在直线上是否存在一点，使∽，若存在，求点坐标；若不存在，请说明理由．‎ ‎19.(2008 湖南 怀化)如图9，已知正比例函数与反比例函数的图象交于两点．‎ ‎（1）求出两点的坐标；‎ ‎（2）根据图象求使正比例函数值大于反比例函数值的的范围；‎ ‎20.(2008 重庆)已知：如图，反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）.‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）求直线BC的解析式.‎ ‎21．（08绵阳市）已知如图，点A（m，3）与点B（n，2）关于直线y = x对称，且都在反比例函数 的图象上，点D的坐标为（0，－2）．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）若过B、D的直线与x轴交于点C，求sin∠DCO的值．‎ ‎22．（08厦门市）已知一次函数与反比例函数的图象交于点和．‎ ‎（1）求反比例函数的关系式；‎ ‎（2）求点的坐标；‎ ‎（3）在同一直角坐标系中画出这两个函数图象的示意图，并观察图象回答：当为何值时，一次函数的值大于反比例函数的值？‎ ‎23.（2008福建省泉州市）已知反比例函数（k为常数，k≠0）的图象经过P(3,3),O为坐标原点。‎ ‎（1）求k的值；‎ ‎（2）过点P作PM⊥x轴于M,若点Q在反比例函数图象上，并且,试求Q点的坐标。‎ ‎24.（2008年四川省南充市）如图，已知，是一次函数的图像和反比例函数的图像的两个交点．‎ ‎（1）求反比例函数和一次函数的解析式；‎ ‎（2）求直线与轴的交点的坐标及三角形的面积．‎ O x y A B C 反比例函数答案 一.选择题 ‎1.A 2.C 3.D 4.C 5.D 6.D 7.C 8.B 9.C 10.A 11.B 12.B 13.C 14.B 15.A 16.B 17.C 18.D 19.A 20.C 21.C 22.C 23.C 24.B 25.A 26.C 27.B 28.B 29.D 30.B 31.D 32.C 33.B 34.D 35.D 36. 37.B 二.填空题 ‎1. 2. 答案不唯一，x128‎ ‎∴能提前28天完成任务。‎ ‎12．（1）y＝0.5x＋１，y＝（2）－６4‎ ‎22.（本小题满分8分）（2008广东肇庆市）‎ 已知点A（2，6）、B（3，4）在某个反比例函数的图象上.‎ ‎（1） 求此反比例函数的解析式；‎ ‎ （2）若直线与线段AB相交，求m的取值范围.‎ ‎13．解：（1）设所求的反比例函数为， ‎ 依题意得: 6 =，‎ ‎∴k=12． （2分）‎ ‎∴反比例函数为． （4分）‎ ‎（2） 设P（x，y）是线段AB上任一点，则有2≤x≤3，4≤y≤6． （6分）‎ ‎∵m = ， ∴≤m≤． ‎ 所以m的取值范围是≤m≤3． （8分） ‎ ‎14. 解：设A点的坐标为（x,y）,由题意得2x+2y=8,‎ 整理得y= 4-x 即A的坐标为（x,4-x）,把A点代入 中，解得x=1或x=3‎ ‎ 由此得到A点的坐标是（1,3）或（3,1）‎ ‎　又由题意可设定直线的解析式为y=x+b（b≥0）‎ ‎　把（1,3）点代入y=x+b，解得　b＝2‎ ‎　把（3,1）点代入y=x+b，解得　b=－2，不合要求，舍去 所以直线的解析式为y=x+2‎ ‎14.设f，v之间的关系式为 当v=50时，f=80，故得k=4000，所以。‎ 当v=100时，f=40（度）。‎ 答：略。‎ ‎15. 解：（1）设一次函数的关系式为，反比例函数的关系式为，‎ 反比例函数的图象经过点，‎ ‎．‎ 所求反比例函数的关系式为．‎ O ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎6‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-5‎ ‎-6‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-5‎ ‎-6‎ x y Q（2，-3）‎ P（-3，2）‎ 将点的坐标代入上式得，‎ 点的坐标为．‎ 由于一次函数的图象过 和，‎ 解得 所求一次函数的关系式为．‎ ‎（2）两个函数的大致图象如图．‎ ‎（3）由两个函数的图象可以看出．‎ 当和时，一次函数的值大于反比例函数的值．‎ 当和时，一次函数的值小于反比例函数的值．‎ ‎16. 解：（1）；；．‎ ‎（2）作轴于，连和．‎ 的坐标为，，．‎ 在的东南方向上，．‎ ‎，．又．‎ 为正三角形．．‎ y x A　‎ B　‎ O　‎ ‎1　‎ ‎1　‎ ‎　‎ ‎　‎ C　‎ ‎(百米)　‎ ‎(百米)　‎ D ‎．‎ 由条件设：教练船的速度为，两船的速度均为4．‎ 则教练船所用的时间为：，‎ 两船所用的时间均为：．‎ ‎，，．‎ 教练船没有最先赶到．‎ ‎17. 解：因为B（－1，m）在上， 所以 所以点B的坐标为（－1，－4） 2分 又A、B两点在一次函数的图像上， ‎ 所以 5分 所以所求的一次函数为y=2x-2 6分 ‎18.‎ 解：(1) ∵双曲线过点 ‎∴‎ ‎∵双曲线过点 ‎∴‎ 由直线过点得,解得 ‎∴反比例函数关系式为,一次函数关系式为.‎ ‎(2)存在符合条件的点,.理由如下:‎ ‎∵∽‎ ‎∴∴，如右图,设直线与轴、轴分别相交于点、,过点作轴于点,连接，则,‎ 故,再由得,从而,因此,点的坐标为.‎ ‎19.‎ 解：（1）解方程组得，‎ 所以A、B两点的坐标分别为：A（1，1）、B（－1，－1）‎ ‎（2）根据图象知，当或时，正比例函数值大于反比例函数值 ‎20. 解：（1）设所求反比例函数的解析式为：．‎ 点在此反比例函数的图象上，‎ ‎，．‎ 故所求反比例函数的解析式为：．‎ ‎（2）设直线的解析式为：．‎ 点的反比例函数的图象上，点的纵坐标为1，设，‎ ‎，．‎ 点的坐标为．‎ 由题意，得 解得：‎ 直线的解析式为：．‎ ‎21. 21．（1）∵ A（m，3）与B（n，2）关于直线y = x对称，‎ ‎∴ m = 2，n = 3， 即 A（2，3），B（3，2）．‎ 于是由 3 = k∕2，得 k = 6． 因此反比例函数的解析式为．‎ ‎（2）设过B、D的直线的解析式为y = kx + b．‎ ‎∴ 2 = 3k + b，且 －2 = 0 · k + b． 解得k =，b =－2．‎ 故直线BD的解析式为 y =x－2．‎ ‎∴ 当y = 0时，解得 x = 1.5．‎ 即 C（1.5，0），于是 OC = 1.5，DO = 2．‎ 在Rt△OCD中，DC =．‎ ‎∴ sin∠DCO =．‎ 说明：过点B作BE⊥y轴于E，则 BE = 3，DE = 4，从而 BD = 5，sin∠DCO ‎ ‎= sin∠DBE =．‎ P O Q x y ‎1‎ ‎2‎ ‎2‎ ‎1‎ ‎-1‎ ‎-2‎ ‎-2‎ ‎-1‎ ‎22．解：（1）设反比例函数关系式为，‎ 反比例函数图象经过点．‎ ‎． 2分 反比例函数关第式． 3分 ‎（2）点在上，‎ ‎． 5分 ‎． 6分 ‎（3）示意图． 8分 当或时，一次函数的值大于反比例函数的值． 10分 ‎23.‎ 解：（1）将点代入中，得k=9; ‎ ‎(2) 设Q点的纵坐标为y,则，解得：y=4‎ 将y=4，k=9代入中，得.Q ‎24. 解：（1）在上 ‎．‎ 反比例函数的解析式为：． 1分 点在上 ‎ 2分 经过，，‎ 解之得 一次函数的解析式为： 4分 O x y A B C ‎（2）是直线与轴的交点 当时，‎ 点……………………………………………5分 ‎…………………………………………………………6分 ‎ 8分